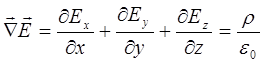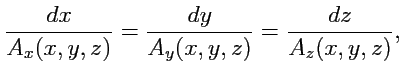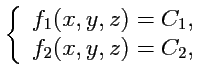8 Вопрос.

Определение поля можно распространить и на векторные величины. Тогда: - если в каждой точке пространства М, принадлежащей некоторой области трехмерного пространства задать вектор , то таким образом будет задано векторное поле.Вектор   (рис. 16) называется вектором поля.

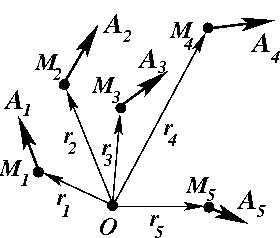
Рис.16. К определению векторного поля.

Примером векторного поля является поле сил тяготения, возникающее в пространстве вокруг материального тела. При этом на пробное тело будет действовать сила, величина и направление которой будет зависеть от положения этого пробного тела в пространстве.

При произвольном течении жидкости скорости частиц в общем случае также будут зависеть от их пространственного положения, образуя, следовательно, векторное поле. Векторное поле является векторной функцией векторного аргумента.

(62)

Если в области определения векторного поля ввести декартову систему координат, то вектор поля можно разложить по ортам  ,  ,  :

(63)

при этом  . Таким образом, задание векторного поля в системе координат означает задание трех независимых функций трех переменных.

     Будем считать, что все функции   непрерывны и дифференцируемы, что обычно выполняется в физических приложениях теории поля. Отдельные точки, где эти условия не выполнены (т. е. вектор поля не определен или испытывает скачки), называются особыми и требуют специального рассмотрения. Геометрической характеристкой векторного поля являются векторные линии, т.е. кривые, в любой точке которых касательная к ним совпадает с вектором поля   (рис. 17). Например, в случае стационарного течения жидкости векторные линии можно рассматривать как траектории движения частиц жидкости, а количество линий будет пропорционально числу частиц.

Рис.17 К определению векторных линий.

Чтобы получить уравнение векторных линий, будем рассматривать сами линии как годограф некоторой вектор-функции  скалярного аргумента. Тогда вектор   будет направлен по касательной к векторной линии в точке с радиус-вектором   (рис. 17). Следовательно, он будет пропорционален вектору поля в этой точке:

(64)

где   - некоторый коэффициент пропорциональности.В системе координат

(65)

Исключив из (65)  , получим систему

которая называется системой дифференциалных уравнений векторных линий. Независимых уравнений в этой системе только два и общее решение может быть представлено в виде:

(67)

и каждая векторная линия, таким образом, будет линией пересечения двух поверхностей   и 

Физический смысл этого утверждения заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы

9 Вопрос.

Дивергенцией или расходимостью векторного поля   называется скалярная функция, определяемая равенством:

Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):

где U – скалярная функция.

Свойства:

Следующие свойства могут быть получены из обычных правил дифференцирования.

Линейность

для любых векторных полей F и G и для всех действительных чисел a и b.

Если φ — скалярное поле, а F — векторное, тогда:

или

Свойство, связывающее векторные поля F и G, заданные в трехмерном пространстве, с ротором:

или

Дивергенция от градиента есть лапласиан:

Дивергенция от ротора:

Теорема остроградсского-Гаусса:

Полный поток вектора напряженности электрического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную

		(1.10)

Пусть в некоторой области пространства известна объемная плотность зарядов r=r(x, y,z) и эта функция непрерывна аналогично представлению о непрерывном распределении вещества.

Рассмотрим в этом пространстве вблизи некоторой точки с координатами x, y,z настолько малый объем dV=dx·dy·dz, что объемная плотность зарядов в нем практически постоянна. Тогда заряд этого объема равен dq=r(x, y,z)·dV

Найдем поток через поверхность граней перпендикулярных оси ОХ:

 

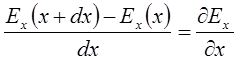
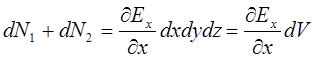
Аналогично можно рассчитать поток через две пары других оснований.

Тогда поток через поверхность всех граней объема:

 

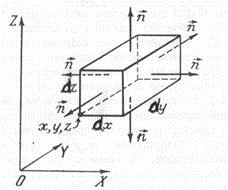
РИС.17   -

Физический смысл дивергенции вектора напряженности в том, что она равна числу линий напряженности выходящих (входящих) из единичного объема, т. е. характеризует расходимость (сходимость) линий напряженности.

Согласно теореме Остроградского-Гаусса в интегральной форме: 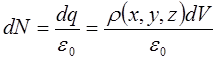 ,   - Дифференциальная форма теоремы Остроградского-Гаусса.

Эта форма применима лишь при условии, если объемная плотность зарядов конечная величина, является следствием интегральной формы и констатирует, что заряды являются источниками (стоками) линий вектора напряженности.

Если ввести векторный оператор Гамильтона:

, 

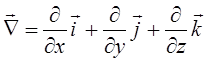Можно записать :