Свойства
Из определения поверхностного интеграла первого рода следует независимость этого интеграла от выбора ориентации векторного поля единичных нормалей к поверхности или, как говорят, от выбора стороны поверхности.
Линейность:
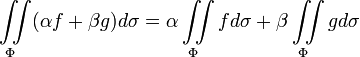;Аддитивность:
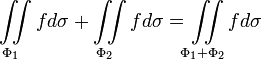;Монотонность:
если
,
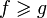то
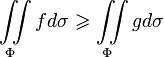
для
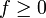если
,
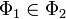то
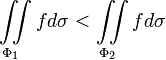
Теорема о среднем для непрерывной функции
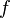и
замкнутой ограниченной поверхности
:
.
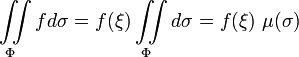Физический смысл поверхностного интеграла 1 рода ∫∫ ρdS Γ — масса тонкой поверхности Γ с поверхностной плотностью ρ .
6 Вопрос.
Криволинейный
интеграл — интеграл,
вычисляемый вдоль какой-либо кривой
на плоскости
или в пространстве.
Утверждения в этой статье приведены
для пространства
,
но могут быть обобщены на пространство
произвольной размерности.
Определение
Предположим, что кривая C задана векторной функцией , где переменная s − длина дуги кривой. Тогда производная векторной функции
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.
|
|
|
Рис.1 |
|
Рис.2 |
Введем
векторную функцию
,
определенную на кривой C,
так, чтобы для скалярной функции
существовал
криволинейный интеграл
.
Такой интеграл
называется
криволинейным
интегралом второго рода
от векторной функции
вдоль
кривой C
и обозначается как
Таким образом, по определению,
где
−
единичный вектор касательной к кривой
C.
Последнюю формулу можно переписать
также в векторной форме:
где
.
Если кривая C
лежит в плоскости Oxy,
то полагая R
= 0,
получаем
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда
Если C − объединение кривых C1 и C2 (рисунок 2 выше), то
Если кривая C задана параметрически в виде
,
то
Если кривая C лежит в плоскости Oxy и задана уравнением
(предполагается,
что R
=0
и t
= x),
то последняя формула записывается в
виде
Физический смысл криволинейного интеграла 2 рода – работа по перемещению тела вдоль кривой в поле переменных сил.
7 Вопрос.
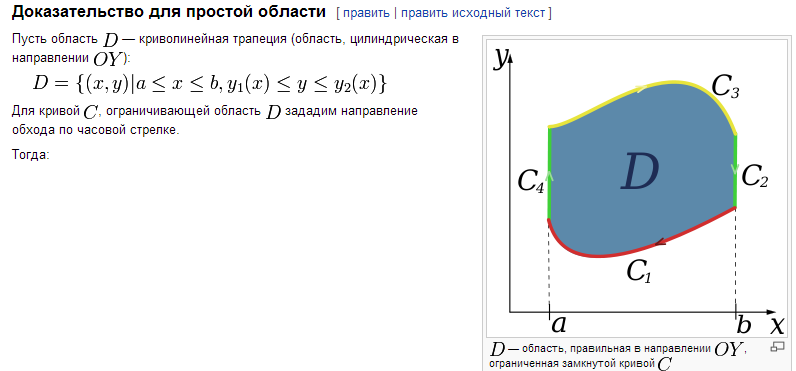
16.3.3.5. Условия независимости криволинейного интеграла от пути интегрирования. В этом разделе будет дан ответ на вопрос: при каких условиях криволинейный интеграл второго рода не зависит от формы пути, соединяющего точки А и В, а определяется только этими точками? Будем предполагать, что в некоторой односвязной области на плоскости заданы непрерывно дифференцируемые функции и , и все рассматриваемые точки, контуры и области принадлежат этой области.
16.3.3.5.1. Теорема 1. Для того, чтобы интеграл не зависел от формы пути, соединяющего точкиА и В, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
Доказательство. Необходимость. Пусть - произвольный замкнутый контур, лежащий в области , А и В - произвольные точки этого контура. Так как, по условию, , то .
Достаточность. Пусть для любого контура выполняется . Пусть , - произвольные точки, и - две различных кривых, соединяющих эти точки. - замкнутый контур, поэтому , что и требовалось доказать.