
- •1 Вопрос.
- •2 Вопрос.
- •Двойной интеграл в полярных координатах
- •Вычисление двойного интеграла в декартовых координатах
- •3 Вопрос.
- •4 Вопрос.
- •5 Вопрос.
- •Свойства
- •6 Вопрос.
- •7 Вопрос.
- •8 Вопрос.
- •9 Вопрос.
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •- (По моему легче учить из тетради по практике. Тут пизда)
- •Дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения второго порядка.
- •Дифференциальные уравнения высших порядков.
- •Системы дифференциальных уравнений вида .
- •13 Вопрос
- •14 Вопрос
- •Метод решения Первый способ
- •Второй способ
- •15 Вопрос
- •16 Вопрос
- •Метод Рунге-Кутта
- •17 Вопрос
- •18 Вопрос
- •26 Вопрос
- •27 Вопрос
- •28 Вопрос
- •2. Необходимый признак сходимости.
- •29 Вопрос
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос
- •33 Вопрос
- •34 Вопрос
- •35 Вопрос
- •36 Вопрос
- •37 Вопрос
- •38 Вопрос Ряды Фурье для четных и нечетных функций. Комплексная форма ряда Фурье.
34 Вопрос
![]()
Разложение функций в степенные ряды…
Если функция раскладывается в степенной ряд (1) в некоторой окрестности точки а, то эта функция является бесконечно дифференцируемой в этой окрестности.
Пример. 
![]() непрерывна
и имеет производные люб 353j97dd ого порядка
и при
непрерывна
и имеет производные люб 353j97dd ого порядка
и при ![]()
![]()

Производная
в нуле: 

Теорема
(о единственности разложения функции
в степенной ряд). Если
в некоторой окрестности точки а ![]()
Степенной
ряд вида ![]() называется рядом Тейлора в
окрестности точки а.
Таким образом, если функция раскладывается
в степенной ряд, то он является рядом
Тейлора. Например:
называется рядом Тейлора в
окрестности точки а.
Таким образом, если функция раскладывается
в степенной ряд, то он является рядом
Тейлора. Например: 
Доказательство. ![]()

Доказано.
Вернёмся
к предыдущему примеру. Если ранее
введённая функция раскладывается в
степенной ряд в некоторой окрестности
точки ![]() противоречие
с возможностью разложения некоторой
функции в некоторой окрестности. Т.е.
одной бесконечной дифференцируемости
функции недостаточно для разложения в
ряд.
противоречие
с возможностью разложения некоторой
функции в некоторой окрестности. Т.е.
одной бесконечной дифференцируемости
функции недостаточно для разложения в
ряд.
Исследуем условия разложимости функции в степенной ряд. Для этого воспользуемся формулой Тейлора:

Отсюда, ![]() раскладывается
в степенной ряд в точке а тогда
и только тогда, когда:
раскладывается
в степенной ряд в точке а тогда
и только тогда, когда:
![]() Таким
образом, вопрос о разложимости связан
с ростом производных функции f.
Укажем достаточные условия на рост
производных для разложимости функций
в степенной ряд.
Таким
образом, вопрос о разложимости связан
с ростом производных функции f.
Укажем достаточные условия на рост
производных для разложимости функций
в степенной ряд.
Теорема. Если ![]() то
то ![]()
 .
.
Доказательство.

Убедимся,
что ![]() Удобнее
всего для этого рассмотреть ряд и
доказать сходимость
Удобнее
всего для этого рассмотреть ряд и
доказать сходимость ![]() По
признаку Даламбера получаем:
По
признаку Даламбера получаем:
![]() ряд
сходится, и в таком случае предел общего
члена равен нулю.
ряд
сходится, и в таком случае предел общего
члена равен нулю.
1) Разложение элементарных функций в ряды Тейлора-Маклорена.

Последнее разложение получено почленным дифференцированием предыдущего разложения.


35 Вопрос
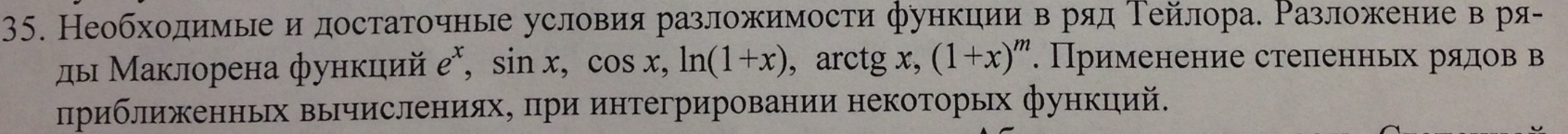
необходимое и достаточное условия разложимости функции в ряд тейлора
Рассмотрим
задачу, обратную поставленной в разд.
30.4. Пусть функция![]() бесконечно
дифференцируема в т.
бесконечно
дифференцируема в т.![]() Составим
для
Составим
для
нее
ряд Тейлора. Его сумма не
всегда будет совпадать с функцией ![]() Например,
функция
Например,
функция![]() бесконечно
дифференцируема при х = 0, причем
бесконечно
дифференцируема при х = 0, причем![]() поэтому
для нее ряд
поэтому
для нее ряд
Маклорена![]() Его
сумма
Его
сумма![]() при
х
при
х![]() 0.
Выясним, при каких условиях
0.
Выясним, при каких условиях![]()
О: Многочленом Тейлора степени п называется частичная сумма
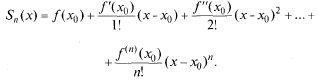
Остаточным членом ряда Тейлора называется
![]() (30.8)
(30.8)
Т:
Для того чтобы бесконечно дифференцируемая
в т.![]() функция
функция![]() являлась
суммой составленного для нее ряда
Тейлора (30.6), необходимо и достаточно,
чтобы
являлась
суммой составленного для нее ряда
Тейлора (30.6), необходимо и достаточно,
чтобы![]()
Используя
определение сходящегося ряда и выражение
(30.8), имеем следующую цепочку: ![]() —
сумма (30.6)
—
сумма (30.6)![]()
![]()
Приведем запись остаточного члена в форме Лагранжа [4. С. 168]:
![]() (30.9)
где
(30.9)
где![]() находится
между
находится
между![]() и
х.
и
х.
36 Вопрос

19.4.1.
Числовые ряды с комплексными членами. Все
основные определения сходимости,
свойства сходящихся рядов, признаки
сходимости для комплексных рядов ничем
не отличаются от действительного
случая.
19.4.1.1.
Основные определения.
Пусть дана бесконечная последовательность
комплексных чисел z1, z2, z3,
…, zn,
… .Действительную часть числа zn будем
обозначать an,
мнимую - bn(т.е. zn = an + i bn, n =
1, 2, 3, …).
Числовой
ряд -
запись
вида 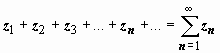 .
Частичные суммы ряда: S1 = z1, S2 = z1 + z2, S3 = z1 + z2 + z3, S4 = z1 + z2 + z3 + z4,
…, Sn = z1 + z2 + z3 +
… + zn,
…
Определение. Если
существует предел S последовательности
частичных сумм ряда при n →
∞, являющийся собственным комплексным
числом, то говорят, что ряд сходится;
число S
называют
суммой ряда и пишут S = z1 + z2 + z3 +
… + zn +
… или S =
.
Частичные суммы ряда: S1 = z1, S2 = z1 + z2, S3 = z1 + z2 + z3, S4 = z1 + z2 + z3 + z4,
…, Sn = z1 + z2 + z3 +
… + zn,
…
Определение. Если
существует предел S последовательности
частичных сумм ряда при n →
∞, являющийся собственным комплексным
числом, то говорят, что ряд сходится;
число S
называют
суммой ряда и пишут S = z1 + z2 + z3 +
… + zn +
… или S = ![]() .
Найдём
действительные и мнимые части частичных
сумм:
Sn = z1 + z2 + z3 +
… + zn =
(a1 + i b1)
+ (a2 + i b2)
+ (a3 + i b3)
+ … + (an + i bn)
= (a1 + a2 + a3 +…+ an)
+
+ i(b1 + b2 + b3 +
... + bn)
= σn + iτn,
где символами σn и
τn обозначены
действительная и мнимая части частичной
суммы. Числовая последовательность
сходится тогда и только тогда, когда
сходятся последовательности, составленные
из её действительной и мнимой частей.
Таким образом, ряд с комплексными членами
сходится тогда и только тогда, когда
сходятся ряды, образованные его
действительной и мнимой частями. На
этом утверждении основан один из способов
исследования сходимости рядов с
комплексными членами.
.
Найдём
действительные и мнимые части частичных
сумм:
Sn = z1 + z2 + z3 +
… + zn =
(a1 + i b1)
+ (a2 + i b2)
+ (a3 + i b3)
+ … + (an + i bn)
= (a1 + a2 + a3 +…+ an)
+
+ i(b1 + b2 + b3 +
... + bn)
= σn + iτn,
где символами σn и
τn обозначены
действительная и мнимая части частичной
суммы. Числовая последовательность
сходится тогда и только тогда, когда
сходятся последовательности, составленные
из её действительной и мнимой частей.
Таким образом, ряд с комплексными членами
сходится тогда и только тогда, когда
сходятся ряды, образованные его
действительной и мнимой частями. На
этом утверждении основан один из способов
исследования сходимости рядов с
комплексными членами.
Абсолютная сходимость.
Определение. Ряд
называется абсолютно
сходящимся,
если сходится ряд  ,
составленный из абсолютных величин его
членов.
Так
же, как и для числовых действительных
рядов с произвольными членами, легко
доказать, что если сходится ряд
,
составленный из абсолютных величин его
членов.
Так
же, как и для числовых действительных
рядов с произвольными членами, легко
доказать, что если сходится ряд 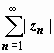 ,
то обязательно сходится ряд
.
(|an|
≤ |zn|,
|bn|
≤ |zn|,
поэтому ряды, образованные действительной
и мнимой частями ряда
,
сходятся абсолютно). Если ряд
сходится,
а ряд
расходится,
то ряд
называется
условно сходящимся.
Ряд
-
ряд с неотрицательными членами, поэтому
для исследования его сходимости можно
применять все известные признаки ( от
теорем сравнения до интегрального
признака Коши).
,
то обязательно сходится ряд
.
(|an|
≤ |zn|,
|bn|
≤ |zn|,
поэтому ряды, образованные действительной
и мнимой частями ряда
,
сходятся абсолютно). Если ряд
сходится,
а ряд
расходится,
то ряд
называется
условно сходящимся.
Ряд
-
ряд с неотрицательными членами, поэтому
для исследования его сходимости можно
применять все известные признаки ( от
теорем сравнения до интегрального
признака Коши).
Свойства
сходящихся рядов. Для
сходящихся рядов c комплексными
членами справедливы все свойства рядов
с действительными членами:
Необходимый
признак сходимости ряда. Общий
член сходящегося ряда стремится к нулю
при n →
∞.
Если
сходится ряд
,
то сходится любой его остаток, Обратно,
если сходится какой-нибудь остаток
ряда, то сходится и сам ряд.
Если
ряд сходится, то сумма его остатка
после n-го
члена стремится к нулю при n →
∞.
Если
все члены сходящегося ряда умножить на
одно и то же число с,
то сходимость ряда сохранится, а сумма
умножится на с.
Сходящиеся
ряды (А)
и (В)
можно почленно складывать и вычитать;
полученный ряд тоже будет сходиться, и
его сумма равна SA ± SB .
Если
члены сходящегося ряда сгруппировать
произвольным образом и составить новый
ряд из сумм членов в каждой паре круглых
скобок, то этот новый ряд тоже будет
сходиться, и его сумма будет равна сумме
исходного ряда.
Если
ряд сходится абсолютно, то при любой
перестановке его членов сходимость
сохраняется и сумма не изменяется.
Если
ряды (А)
и (В)
сходятся абсолютно к своим суммам SА и SB,
то их произведение при произвольном
порядке членов тоже сходится абсолютно,
и его сумма равна SА·SА.
19.4.2.
Степенные комплексные
ряды.
Определение. Степенным
рядом с комплексными членами называется
ряд вида  , где a0, a1, a2,
…, an, -
постоянные комплексные числа (коэффициенты
ряда), z0 -
фиксированное комплексное число (центр
круга сходимости). Для любого численного
значения z ряд
превращается в числовой ряд с комплексными
членами, сходящийся или расходящийся.
Если ряд сходится в точке z,
то эта точка называется точкой сходимости
ряда. Степенной ряд имеет по меньшей
мере одну точку сходимости - точку z0.
Совокупность точек сходимости называется
областью сходимости ряда.
Как
и для степенного ряда с действительными
членами, все содержательные сведения
о степенном ряде содержатся в теореме
Абеля.
, где a0, a1, a2,
…, an, -
постоянные комплексные числа (коэффициенты
ряда), z0 -
фиксированное комплексное число (центр
круга сходимости). Для любого численного
значения z ряд
превращается в числовой ряд с комплексными
членами, сходящийся или расходящийся.
Если ряд сходится в точке z,
то эта точка называется точкой сходимости
ряда. Степенной ряд имеет по меньшей
мере одну точку сходимости - точку z0.
Совокупность точек сходимости называется
областью сходимости ряда.
Как
и для степенного ряда с действительными
членами, все содержательные сведения
о степенном ряде содержатся в теореме
Абеля.
 Теорема
Абеля. Если
степенной ряд сходится в точке z1 ≠ z0,
то он абсолютно сходится в любой точке
круга | z - z0|
< | z1 - z0|;
Если
этот ряд расходится в точке z2,
то он расходится в любой точке z,
удовлетворяющей неравенству | z - z0|
> | z2 - z0| (т.е.
находящейся дальше от точки z0,
чем z2).
Доказательство
дословно повторяет доказательство
раздела 18.2.4.2.
Теорема Абеля для
ряда с действительными членами.
Из
теоремы Абеля следует существование
такого неотрицательного действительного
числа R,
что ряд абсолютно сходится в любой
внутренней точке круга радиуса R с
центром в точке z0,
и расходится в любой точке вне этого
круга. Число R называется радиусом
сходимости,
круг - кругом
сходимости.
В точках границы этого круга - окружности
| z - z0|
= R радиуса R с
центром в точке z0 -
ряд может и сходиться, и расходиться. В
этих точках ряд из модулей имеет вид
Теорема
Абеля. Если
степенной ряд сходится в точке z1 ≠ z0,
то он абсолютно сходится в любой точке
круга | z - z0|
< | z1 - z0|;
Если
этот ряд расходится в точке z2,
то он расходится в любой точке z,
удовлетворяющей неравенству | z - z0|
> | z2 - z0| (т.е.
находящейся дальше от точки z0,
чем z2).
Доказательство
дословно повторяет доказательство
раздела 18.2.4.2.
Теорема Абеля для
ряда с действительными членами.
Из
теоремы Абеля следует существование
такого неотрицательного действительного
числа R,
что ряд абсолютно сходится в любой
внутренней точке круга радиуса R с
центром в точке z0,
и расходится в любой точке вне этого
круга. Число R называется радиусом
сходимости,
круг - кругом
сходимости.
В точках границы этого круга - окружности
| z - z0|
= R радиуса R с
центром в точке z0 -
ряд может и сходиться, и расходиться. В
этих точках ряд из модулей имеет вид  .
Возможны такие случаи:
1.
Ряд
сходится.
В этом случае в любой точке окружности
| z - z0|
= R ряд
сходится абсолютно.
2.
Ряд
расходится,
но его общий член |an|·R n →
0 при n →
∞. В этом случае в некоторых точках
окружности ряд может сходиться условно,
в других - расходиться, т.е. каждая точка
требует индивидуального
исследования.
3.
Ряд
расходится,
и его общий член |an|·R n не
стремится к нулю при n →
∞. В этом случае ряд расходится в любой
точке граничной окружности.
.
Возможны такие случаи:
1.
Ряд
сходится.
В этом случае в любой точке окружности
| z - z0|
= R ряд
сходится абсолютно.
2.
Ряд
расходится,
но его общий член |an|·R n →
0 при n →
∞. В этом случае в некоторых точках
окружности ряд может сходиться условно,
в других - расходиться, т.е. каждая точка
требует индивидуального
исследования.
3.
Ряд
расходится,
и его общий член |an|·R n не
стремится к нулю при n →
∞. В этом случае ряд расходится в любой
точке граничной окружности.
