
- •1 Вопрос.
- •2 Вопрос.
- •Двойной интеграл в полярных координатах
- •Вычисление двойного интеграла в декартовых координатах
- •3 Вопрос.
- •4 Вопрос.
- •5 Вопрос.
- •Свойства
- •6 Вопрос.
- •7 Вопрос.
- •8 Вопрос.
- •9 Вопрос.
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •- (По моему легче учить из тетради по практике. Тут пизда)
- •Дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения второго порядка.
- •Дифференциальные уравнения высших порядков.
- •Системы дифференциальных уравнений вида .
- •13 Вопрос
- •14 Вопрос
- •Метод решения Первый способ
- •Второй способ
- •15 Вопрос
- •16 Вопрос
- •Метод Рунге-Кутта
- •17 Вопрос
- •18 Вопрос
- •26 Вопрос
- •27 Вопрос
- •28 Вопрос
- •2. Необходимый признак сходимости.
- •29 Вопрос
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос
- •33 Вопрос
- •34 Вопрос
- •35 Вопрос
- •36 Вопрос
- •37 Вопрос
- •38 Вопрос Ряды Фурье для четных и нечетных функций. Комплексная форма ряда Фурье.
32 Вопрос
![]()
Знакопеременный ряд.Теорема Коши о достаточных условиях сходимости знакопеременного ряда.Абсолютно и условно сходящиеся ряды.Свойства абсолютно сходящихся рядов.
О п р е д е л е н и е. Знакопеременный ряд – это ряд с членами разных знаков.
Знакопеременный ряд
 (21)
(21)
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений его членов
 .
(22)
.
(22)
Всякий
абсолютно сходящийся ряд есть ряд
сходящийся. Если ряд ![]() абсолютно
сходится, то ряд, полученный после любой
перестановки его членов, абсолютно
сходится и имеет ту же сумму, что и
исходный ряд.
абсолютно
сходится, то ряд, полученный после любой
перестановки его членов, абсолютно
сходится и имеет ту же сумму, что и
исходный ряд.
Сходящийся
ряд ![]() называется
условно сходящимся, если ряд
называется
условно сходящимся, если ряд  расходится.
Если
ряд
условно
сходится, то при перестановке его членов
сумма ряда может измениться. В частности,
при некоторой перестановке членов
условно сходящегося ряда его можно
превратить в расходящийся ряд.
расходится.
Если
ряд
условно
сходится, то при перестановке его членов
сумма ряда может измениться. В частности,
при некоторой перестановке членов
условно сходящегося ряда его можно
превратить в расходящийся ряд.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
с неотрицательными членами существует такое число , , что, начиная с некоторого номера, выполняется неравенство , то данный ряд сходится. |
Абсолютно сходящимся
рядом называется сходящийся ряд ![]() ,
для которого сходится и ряд
,
для которого сходится и ряд ![]() .
.
Легко
доказать, что из сходимости ряда
вытекает
сходимость ряда ![]() .
По критерию Коши, примененному к
,
получаем:
.
По критерию Коши, примененному к
,
получаем: ![]()
![]() .
Из полученного неравенства следует,
что
.
Из полученного неравенства следует,
что ![]() и
для исходного ряда также выполнен
критерий Коши, следовательно он сходится.
и
для исходного ряда также выполнен
критерий Коши, следовательно он сходится.
Обозначим ![]() ,
т.е.
,
т.е. ![]() ,
, ![]() .
Очевидны равенства:
.
Очевидны равенства: ![]() .
Рассмотрим ряды
.
Рассмотрим ряды ![]() и
и ![]() .
Если они сходятся, то сходится и ряд
.
Если они сходятся, то сходится и ряд ![]() ,
т.е. ряд абсолютно сходится. Если же
сходятся ряды
,
т.е. ряд абсолютно сходится. Если же
сходятся ряды ![]() ,
то, т.к.
,
то, т.к. ![]() ,
ряды
и
тоже
сходятся. Таким образом, для абсолютной
сходимости необходима и достаточна
сходимость рядов
и
.
,
ряды
и
тоже
сходятся. Таким образом, для абсолютной
сходимости необходима и достаточна
сходимость рядов
и
.
33 Вопрос

.Функциональный ряд.Область сходимости,сумма и остаток функционального ряда.Структура области сходимости степенных рядов.Интегрирование и дифференцирование степенных рядов.
Функциональный
ряд —
ряд, каждым членом которого, в отличие
от числового
ряда,
является не число, а функция ![]() .
.
Сходимость
Ряд
называется сходящимся поточечно, если
последовательность ![]() его
частичных сумм сходится поточечно.
его
частичных сумм сходится поточечно.
Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.
Необходимое условие равномерной сходимости
![]()
Абсолютная и условная сходимость
Ряд ![]() называется
абсолютно сходящимся, если
называется
абсолютно сходящимся, если ![]() сходится.
Абсолютно сходящийся ряд сходится.
сходится.
Абсолютно сходящийся ряд сходится.
Если ряд сходится, а расходится, то ряд называется сходящимся условно.
Теоремы о непрерывности
Последовательность непрерывных в точке функций сходится к функции, непрерывной в этой точке.
Последовательность ![]()
![]() функция
непрерывна
в точке
функция
непрерывна
в точке ![]()
Тогда ![]() непрерывна
в
.
непрерывна
в
.
Ряд непрерывных в точке функций сходится к функции, непрерывной в этой точке.
Ряд 
функция непрерывна в точке
Тогда ![]() непрерывна
в
.
непрерывна
в
.
Теоремы об интегрировании
Теорема о переходе к пределу под знаком интеграла.
функция
интегрируема
на отрезке ![]()
на
Тогда 
Теорема о почленном интегрировании.
функция непрерывна на отрезке
 на
на
Тогда 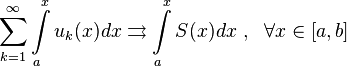
Теоремы о дифференцировании
Теорема о дифференцировании под пределом.
функция непрерывно дифференцируема на отрезке
![]() сходится
сходится
![]() на
отрезке
на
отрезке
Тогда ![]() —
непрерывно дифференцируема на
,
—
непрерывно дифференцируема на
, ![]() на
на
Теорема о почленном дифференцировании.
функция непрерывно дифференцируема на отрезке
![]() сходится
сходится
![]() равномерно
сходится на отрезке
равномерно
сходится на отрезке
Тогда  —
непрерывно дифференцируема на
,
—
непрерывно дифференцируема на
, ![]() на
на
