16 Вопрос

Численное решение задачи Коши для дифференциального уравнения первого порядка методом Эйлера. Ломаная Эйлера. Понятие о методе Рунге-Кутте

Метод Эйлера

Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

где yi+1  это искомое значение функции в точке xi+1.

Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить  yi+1 , если известно yi  в точке хi:

                                                                                             (6.4)

Сравнивая формулу Эйлера с общим выражением, полученным ранее, видно, что для приближенного вычисления интеграла в (6.3) в методе Эйлера используется простейшая формула интегрирования - формула прямоугольников по левому краю отрезка.

Графическая интерпретация метода Эйлера также не представляет затруднений (см. рисунок ниже). Действительно, исходя из вида решаемого уравнения (6.2) следует, что значение   есть значение производной функции y(x) в точке x=xi -    , и, таким образом, равно тангенсу угла наклона каcательной, проведенной к графику функции y(x) в точке x=xi.

 Из прямоугольного треугольника на рисунке можно найти

  ,

откуда и получается формула Эйлера. Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точкеx=xi.

Метод ломаных Эйлера

Пусть дано обыкновенное дифференциальное уравнение

у ‘ = f(x; y)

с начальным условием у(х₀) = у₀.

Выберем достаточно малый шаг h и построим с помощью начального условия последовательность точек х₀; х₀ + h; x₀ + 2h; …; x₀ + nh, после чего искомая интегральная кривая (т.е. решение данного дифференциального уравнения – см. статью «Дифференциальное уравнение») заменяется ломаной (ломаная Эйлера), звенья которой – отрезки прямых линий, определённые на отрезках [x_i; x_i+1], а ординаты концов определяются по формулам

y_i+1 = y_i + hf(x_i; y_i), i = 0; 1; …; n.

Если функция f(x; y) непрерывна, то на фиксированном отрезке [x₀; x₀ + H] последовательность ломаных Эйлера при n → +∞ равномерно  стремится к искомой интегральной кривой у = у(х).

Если функция f(x; y) дифференцируема, погрешность метода ломаных Эйлера достаточно мала.

Метод предложен Л. Эйлером в 1768 году.

Метод Рунге-Кутта

Вновь рассмотрим дифференциальное уравнение

         (1)

с начальным условием   

Классический метод Рунге-Кутта 4-го порядка описывается следующей системой пяти равенств:

           (5)

где

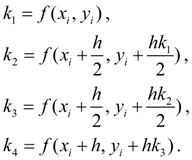
Строго говоря, существует не один, а группа методов Рунге-Кутта, отличающихся друг от друга порядком, т.е. количеством параметров  . В данном случае мы имеем метод 4-го порядка, который является одним из наиболее применяемых на практике, так как обеспечивает высокую точность и в то же время отличается сравнительной простотой. Поэтому в большинстве случаев он упоминается в литературе просто как «метод Рунге-Кутта» без указания его порядка.