
- •1 Вопрос.
- •2 Вопрос.
- •Двойной интеграл в полярных координатах
- •Вычисление двойного интеграла в декартовых координатах
- •3 Вопрос.
- •4 Вопрос.
- •5 Вопрос.
- •Свойства
- •6 Вопрос.
- •7 Вопрос.
- •8 Вопрос.
- •9 Вопрос.
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •- (По моему легче учить из тетради по практике. Тут пизда)
- •Дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения второго порядка.
- •Дифференциальные уравнения высших порядков.
- •Системы дифференциальных уравнений вида .
- •13 Вопрос
- •14 Вопрос
- •Метод решения Первый способ
- •Второй способ
- •15 Вопрос
- •16 Вопрос
- •Метод Рунге-Кутта
- •17 Вопрос
- •18 Вопрос
- •26 Вопрос
- •27 Вопрос
- •28 Вопрос
- •2. Необходимый признак сходимости.
- •29 Вопрос
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос
- •33 Вопрос
- •34 Вопрос
- •35 Вопрос
- •36 Вопрос
- •37 Вопрос
- •38 Вопрос Ряды Фурье для четных и нечетных функций. Комплексная форма ряда Фурье.


1 Вопрос.
Определение:
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
где R -
область интегрирования в плоскости
Oxy.
Если определенный интеграл ![]() от
функции одной переменной
от
функции одной переменной ![]() выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
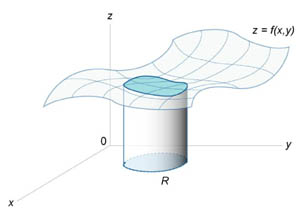
Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу.
Объем цилиндрического тела
Р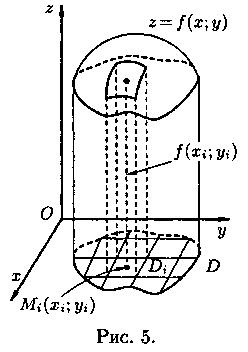 ассмотрим
тело, ограниченное сверху поверхностью
ассмотрим
тело, ограниченное сверху поверхностью![]() снизу
- замкнутой областью D плоскости Оху,
с боков - цилиндрической поверхностью,
образующая которой параллельна оси Oz,
а направляющей служит граница области
D (см. рис. 5). Такое тело называется
цилиндрическим. Найдем его объем V. Для
этого разобьем область D (проекция
поверхности z=ƒ(х;у) на плоскость Оху)
произвольным образом на п областей Di,
площади которых равны
снизу
- замкнутой областью D плоскости Оху,
с боков - цилиндрической поверхностью,
образующая которой параллельна оси Oz,
а направляющей служит граница области
D (см. рис. 5). Такое тело называется
цилиндрическим. Найдем его объем V. Для
этого разобьем область D (проекция
поверхности z=ƒ(х;у) на плоскость Оху)
произвольным образом на п областей Di,
площади которых равны ![]() Рассмотрим
цилиндрические столбики с основаниями
Di, ограниченные сверху кусками поверхности
z=ƒ(х;у) (на рис. 5 один из них выделен).
В своей совокупности они составляют
тело V. Обозначив объем столбика с
основанием Di через ∆Vi,
получим
Рассмотрим
цилиндрические столбики с основаниями
Di, ограниченные сверху кусками поверхности
z=ƒ(х;у) (на рис. 5 один из них выделен).
В своей совокупности они составляют
тело V. Обозначив объем столбика с
основанием Di через ∆Vi,
получим
Возьмем на каждой площадке Di произвольную точку Mi(xi;,yi) и заменим каждый столбик прямым цилиндром с тем же основанием D; и высотой zi=ƒ(хi;уi).
Объем этого цилиндра приближенно равен объему ΔVi цилиндрического
столбика,
т. е.![]() .
Тогда получаем:
.
Тогда получаем: ![]()
Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» Di. Естественно принять предел суммы (7.3) при условии, что число площадок Di неограниченно увеличивается (n -> ∞), а каждая площадка стягивается в точку (maxdi-> 0), за объем V цилиндрического тела, т. е.
![]()
или, согласно равенству (7.2),
![]()
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется
найти массу m плоской пластинки D, зная,
что ее поверхностная плотность g=g(х;у)
есть непрерывная функция координат
точки (х;у). Разобьем пластинку D на п
элементарных частей![]() площади
которых обозначим через ∆Si.
В каждой области D; возьмем произвольную
точку Мi(хi;уi)
и вычислим плотность в ней:
площади
которых обозначим через ∆Si.
В каждой области D; возьмем произвольную
точку Мi(хi;уi)
и вычислим плотность в ней:![]()
Если
области Di достаточно
малы, то плотность в каждой точке (х;у)
є Di мало
отличается от значения g(xi;yi).
Считая приближенно плотность в каждой
точке области Di постоянной,
равной g(xi;yi),
можно найти ее массу ![]() Так
как масса m всей пластинки D равна
Так
как масса m всей пластинки D равна ![]() то
для ее вычисления имеем приближенное
равенство
то
для ее вычисления имеем приближенное
равенство
![]()
Точное значение массы получим как предел суммы (7.5) при условии n ->∞ и max di -> 0:
![]()
или, согласно равенству (7.2),
![]()
Итак, двойной интеграл от функции g(x;у) численно равен массе пластинки, если подынтегральную функцию g(х;у) считать плотностью этой пластинки в точке (х;у). В этом состоит физический смысл двойного интеграла.
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:

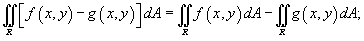
 ,
где k -
константа;
,
где k -
константа;Если
 в
области R,
то
в
области R,
то 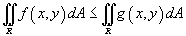 ;
;Если
 в
области R и
в
области R и  (рисунок
4), то
(рисунок
4), то  ;
;Если на R и области R и S являются непересекающимися (рисунок 5), то
 .
Здесь
.
Здесь  означает
объединение этих двух областей
означает
объединение этих двух областей

 .
.

