24.Смещение точек на аэроснимке под влиянием его угла наклона

Рассмотрим два аэроснимка: горизон­тальный Ро и наклон­ный Р. Оба аэросним­ка получены из одного центра фотографирова­ния S (Рис. 35). На­клонный снимок пере­секается с горизон­тальным по линии не­искаженных масштабов h_с h_с.

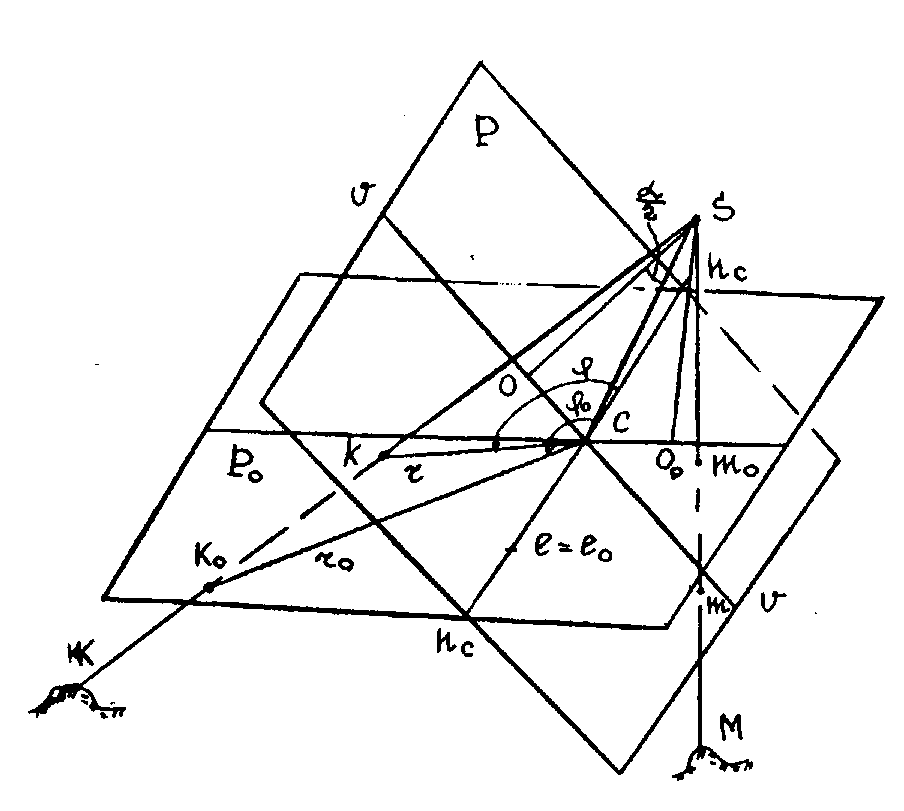
Рассмотрим изобра­жения точек местности К, L, М на горизон­тальном и наклонном снимках. Проведем из точки нулевых искаже­ний c радиус-векторы r и r_o к изображениям точек К, L, М. Углы  и ₀, как сле­дует из предыдущего равны.

Если снимок Р повернуть вокруг линии неискаженных масштабов h_с h_с до совмещения со снимком Р₀ (Рис. 36), то радиус - век­торы r и r_o совпадут, но точка k окажется смещенной относи­тельно точки k_о по радиус - вектору, следовательно наклон аэроснимка вызывает радиальное смещение. Точка k приблизится к точке с, а точка m уда­лится от нее.

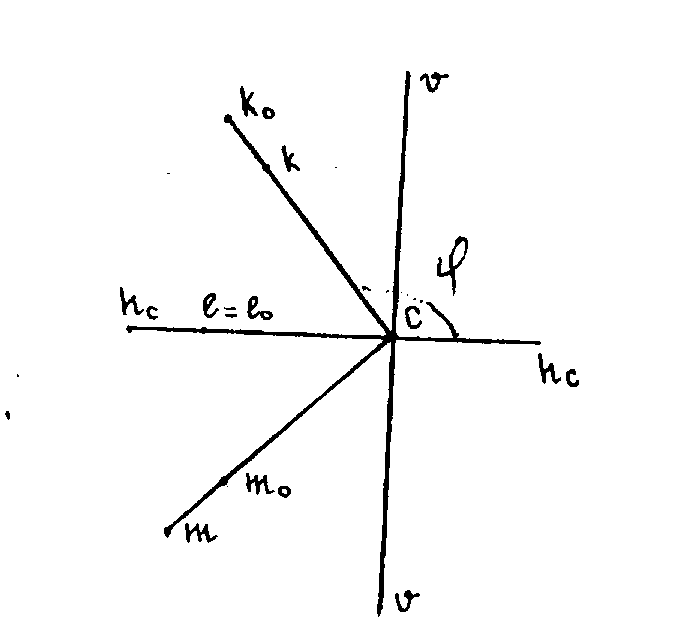
Точка 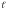зани­мает одинаковое положение на горизонтальном и наклонном снимках. Это следует из того, что масштаб наклонного аэро­снимка выше линии неискажен­ных масштабов меньше масштаба горизонтального аэроснимка, ниже линии неискаженных мас­штабов - больше масштаба го­ризонтального аэроснимка, а на линии h_с h_с масштаб равен 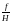. Смещение точки обуслов­ленное наклоном аэроснимка _ будет

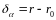(82)

Радиус - векторам r и r_o на местности соответствует ра­диус - вектор R, который можно вычислить по формуле

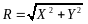
где

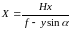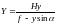,(47) (49)

следовательно

,

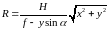здесь 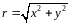тогда

. (83)

На основании Рис.37 можно записать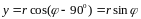 . Подставим полученное значение в формулу (83), будем иметь

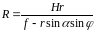. (84)

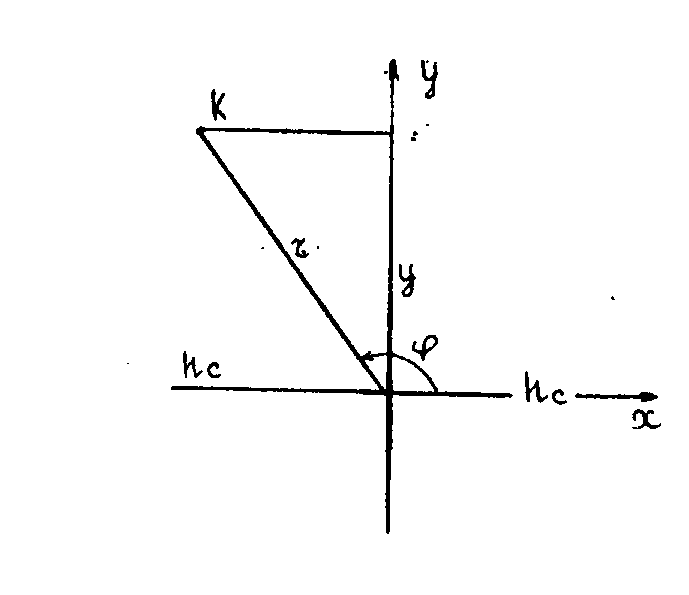
Если бы снимок был горизон­тален, то есть =0°, то вмес­то r имели бы r₀, и значе­ние R вычислялось по формуле

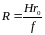(85)

Поделим равенство (84) на ра­венство (85), получим

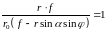(86)

Из- формулы (82) найдем r₀, подставим его в формулу (86) и решим полученное уравнение относительно _

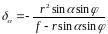(87)

Выражение (87) показывает величину смещения точки из - за наклона аэроснимка.

При малых углах наклона, то есть при плановой аэросъемке можно использовать приближенную формулу

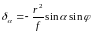(88)

25.Смещение точек на аэроснимке под влияние рельефа местности

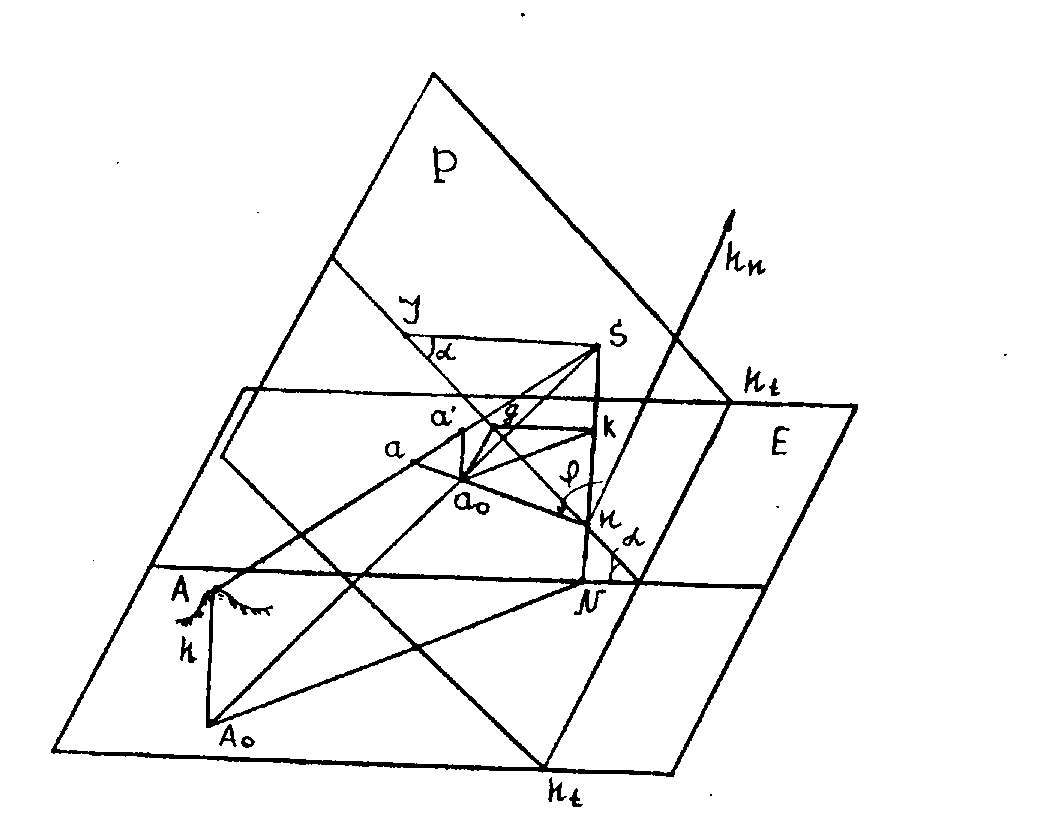
Точка A_о это ортогональная проекция точки А на горизон­тальную плоскость Е. Изображение точки А будет в точке a, расположенной на радиус - векторе r=an, который проходит через точку надира снимка n, аа₀- перспектива вертикальной линии AA₀.

Если бы точка А не имела превышения, то изображение ее было бы в точке a₀, таким образом отрезок aa₀ является смещением точки аэроснимка из - за влияния рельефа, то есть .

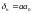Следовательно рельеф местности вызывает смещения контурных то­чек аэроснимка по направлениям проходящим через точку надира n. Полярными координатами точки a, будут радиус-вектор r=na и полярный угол . Полюсом является точка надира n, а по­лярной осью - надирная горизонталь h_n h_n.

Для вывода формулы смещения точек под влиянием рельефа вы­полним вспомогательные построения. Из точки a₀ проведем го­ризонталь до встречи с главной вертикалью, получим точку q. Проведем линию из точки a₀ параллельную A₀N до пересечения с отвесной прямой SN, получим точку К. Точки К и q соединим прямой, которая будет перпендикулярна к линии SN. Получен­ная плоскость a₀qК параллельна плоскости Е. И через точку a₀ проведем прямую параллельную SN, получим 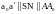. Рассмотрим подобные треугольники 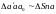. Из по­добия этих треугольников можно записать отношение

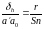
Решим полученное равенство относительно

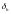
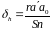(89)

В формуле (89) 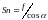(32), а величину а'а₀ найдем из подобных треугольников

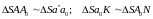
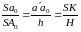, откуда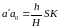 , (90)

в свою очередь 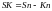(91)

Из прямоугольного треугольника 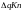можно записать

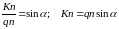. (92)

величину qn найдем из прямоугольного треугольника

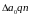
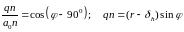, (93)

следовательно

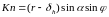, (94)

Подставим формулы (32) и (94) в равенство (91)

.

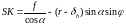Полученное значение SК подставим в формулу (90)

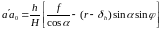. (95)

Подс значение a'a₀ из формулы (95) и Sn из формулы (32) в выражение (89).

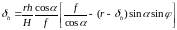
В полученном равенстве вынесем за скобку величину

,

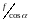
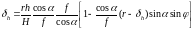где 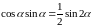, тогда

Перенесем члены содержащие в левую сторону

,

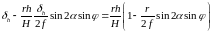Решим полученное равенство относительно .

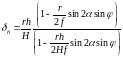Формула (96) выражает величину смещения точки из - за релье­фа местности.

При r=0, =0, следовательно рельеф не вызывает смещения точки, совпадающей с точкой надира.При = 0, 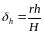(97)

На горизонтальном аэроснимке смещения точек прямо пропорцио­нальны их расстояниям от главной точки (так как на горизон­тальном аэроснимке главная

точка совпадает с точкой надира), превышению точек местности относительно начальной плоскости и обратно пропорциональны высоте фотографирования.