22.Масштаб наклонного снимка равнинной местности

масштаб наклонного снимка равнинной местности изменяется с изменением положения и направления измеряемого отрезка.

Для вывода формулы масштаба наклонного аэроснимка воспользу­емся уравнением связи координат точек картинной и предметной плоскостей, когда начало координат находится в точке нулевых искажений. На основании выражения (47) запишем отношение

(65)

Как видно отношение (65) будет меняться с изменением орди­наты y.

Для горизонтали, проходящей через точку нулевых искажений у=0, поэтому

, (64)

то есть масштаб горизонтали, проходящей через точку нулевых ис­кажений равен масштабу горизонтального аэроснимка, поэтому дан­ная горизонталь носит название линии неискаженных масштабов.

• Для главной горизонтали

(33)

, поэтому

. (67)

. (68)

• Для надирной горизонтали

(69)

.

• Для линии действительного горизонта ,

. (71)

• Для основания картины .

. (71)

Масштаб аэроснимка по главной вертикали или по произвольно­му направлению не может быть выпажен такими простыми зависи­мостями, так как он непрерывно изменяется при переходе от од­ной точки к другой. В общем случае масштаб аэроснимка следует выражать как отноше­ние бесконечно малых отрезков

Общую формулу масшта­ба в этом случае мож­но записать

Здесь начало коорди­нат находится в глав­ной точке схода I (Рис.32).

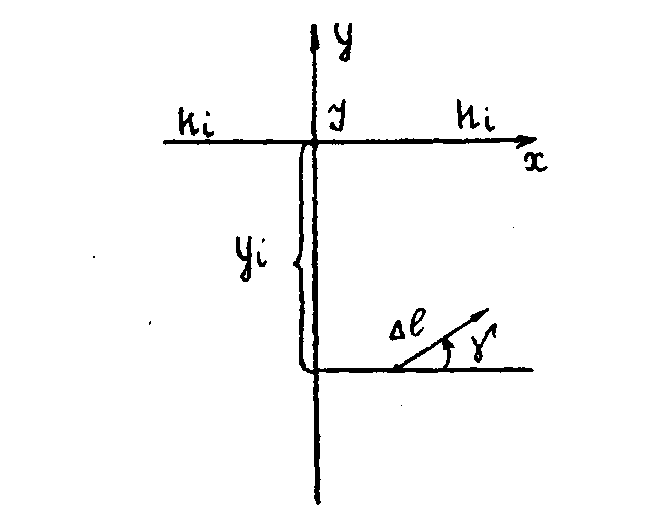
23.Искажение направлений под влиянием наклона снимка

Приняв за полюс точку нулевых искажений с, а за полярную ось - линию неискаженных масштабов h_ch_c будем иметь полярные координаты: угол  (Рис.33) и радиус - вектор r=ca. Про­ведем из точки а произвольное направление аi, составляющее с горизонталью h_ah_a угол  .

Найдем точку на местности соответствующую точке снимка a. Для этого продолжим линию ai до пересечения с линией основа­ния картины h_th_t, получим точку а_о. Центр проекции S соеди­ним с точкой i и из точки а_о проведем прямую параллельную Si .

Получим линию на местности, соответствующую линии аэроснимка ai на которой находится точка местности A. Для определения положения точки А проведем проектирующий луч Sа. который в пересечении с построенной прямой даст искомую точку. Через точку А проведем прямую перпендикулярно линии направления съемки VV. Угол между линиями h_ah_a и ААо обозначим '. В плоскости действи­тельного горизонта G углу ' равен угол между линией дейс­твительного горизонта h_ih_i и линией Si, так как прямая h_ah_a параллельна линии действительного горизонта, а прямая Si параллельна линии ААо. В общем случав угол ' не равен углу . Искажение направления вызванное наклоном аэроснимка  будет . (73)

Плоскость действительного горизонта G в которой лежат лучи SI и Si повернем вокруг линии действительного горизонта h_ih_i до совмещения с плоскостью снимка Р и так как треуго­льник равнобедренный точка S совпадает с точкой с

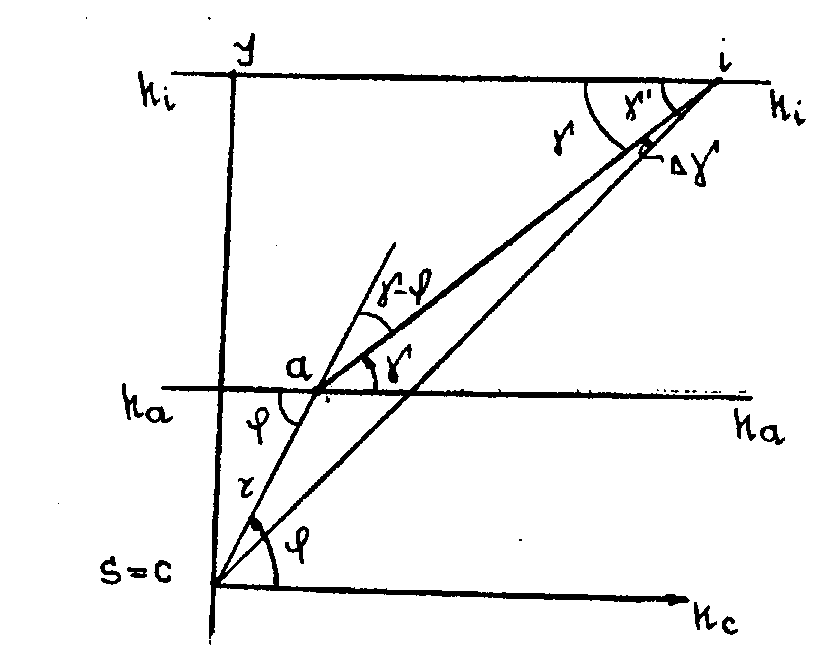
Используя теорему си­нусов напишем

; .

Из прямоугольного треугольника имеем

, где ,следовательно .

Подставим полученное значение Si в формулу (74)

или .

Поделим обе части уравнения (76) на

Перенесем члены содержащие влево

. (77)

Решим равенство (77) относительно

. (78)

Как видно из выражения (78) величина искажения зависит от поляр­ных координат точки, из которой проведено направление r, и от угла . При r=0, = 0, то есть наклон аэроснимка не искажает направлений выходящих из точки нулевых искажений c, следовательно, в этой точке углы на снимке равны соответственным углам на местнос­ти. Поэтому точка c и называется точкой нулевых искажений.

Для плановых аэроснимков формулу (78) можно упростить, отбросив в знаменателе второй член как малую величину, тогда

. (79)

Определим искажения направлений в главной точке о и точке надира n для планового аэроснимка. Для главной точки и =90°. Подставим в (79)

. (80)

Для точки надира и =270°, тогда

. (81)

Таким образом в случае равнинной местности и при наличии наклона аэроснимка будут происходить искажения направлений.