4 4. Связь между продольными параллаксами на горизонтальном и наклонном снимках

При идеальном случае продольный параллакс равен

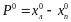(38)

зависимость между абсциссами горизонтального и наклонного снимков имеет вид

(39)

Для снимка необходимо в правую часть выражения (39) ввести поправку за превышение правого конца базиса фотографирования

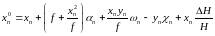(40)

На плановых аэроснимках 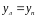.Кроме того, вместо координаты x_л в выражение (39) подставим , тогда

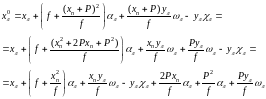(41)

Обозначим ,

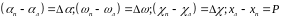тогда, с учетом выражений (40) и (41) формула (38) будет

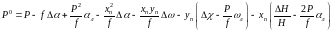(42)

1ая поправка к параметру Р яв-ся постоянной для всех точек данной стереопары. 2ую поправку можно считать пос­тоянной, если рельеф местности небольшой. Остальные поп­р. зависят от положения т-и на правом аэроснимке.

45. Уравнение ориентирования на стереометре

Продольный параллакс этой точки обозна­чим P₁. Для любой другой точки стереопары можно напи­сать равенство

(43)

где Р - разность продольных параллаксов.

С учетом выражения (43) зависимость (42) будет иметь вид

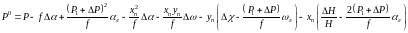Раскроем скобки, получим

(44)

В выражении в дальнейшем учитывать не будем, так как он мал.

Для главной точки правого снимка o_п (рис.16) 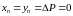. Следовательно зависимость (44) для этой точки будет представлена в следующем виде

(45)

Вычтем из равенства (44) равенство (45), тогда разность про­дольных параллаксов Р будет

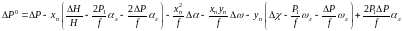Поправки, вводимые коррекционными механизмами, делят на две группы:

а) поправки первого порядка

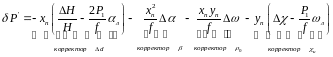
б) поправки второго порядка

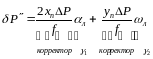
При небольшом рельефе поправками второго порядка пренебрегают. Рассмотрим устройство и работу основных корректоров.

46. Теория коррекционных механизмов стереометра

Корректор d

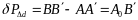(47)

Из подобия треугольников 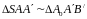напишем

или

(48)

Корректор призван решать формулу

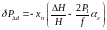(49)

Приравняем выражения (48) и (49)

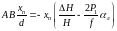(50)

Если в выражении (50) величина

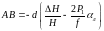(51)

то, очевидно, корректор d решает свою задачу.

Корректор 

Корректор  состоит из двух линеек L₁ и L₂ (рис. 22), вращающейся вок­руг точки S. Линейка L₁ шарнирно связана с общей кареткой, а линейка L₂ – с кареткой правого аэроснимка. Линейки могут взаимно разворачиваться на угол  и совместно на угол . При отвесном положении линейки L₂ к оси X стереометра правая нить совпадает с главной точкой правого аэроснимка. Линейка L₂ корректора  в тоже время является линейкой L корректора d. Оба этих корректора объединены в один узел только конструктивно. Каждый корректор решает только свою задачу.

Перемещение общей каретки на расстояние AA'=x вызывает перемещение правого аэроснимка на величину BB'=P_, следовательно

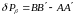(52)

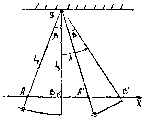
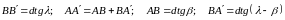
(53)

Приведем выражение в скобках уравнения (53) к общему знаменателю

,

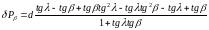(54)

Для плановых аэроснимков, величины, вводимые корректорами, малы, поэтому можно принять BB'=x_п и следовательно

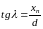(55)

Кроме того, вместо tg при малом развороте линеек можно использовать , а членом tg tg в знаменателе выражения (54) пренебречь, тогда

(56)

В формуле (56) ² – величина второго порядка малости, которой тоже пренебрегают и выражение (56) будет иметь вид

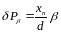(57)

В соответствии с теорией корректор  должен решать следующее выражение

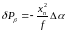(58)

Приравняв формулы (57) и (58), получим

(59)

Если на корректоре  установить значение, вычисленное по формуле (59), то он будет решать свою задачу.

Корректор 

Корректор  состоит из рычага r, скрепленного под прямым углом с нитедержателем NN(N'N') и линейки L, которую можно наклонять к оси X прибора на угол 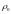вокруг оси Q (рис. 23).

Рычаг r в точке R(R') оканчивается роликом.

В начальном положении ось Q совпадает с точкой R. В это время правая нить проходит через главную точку правого аэроснимка перпендикулярно оси X прибора. При смещении общей каретки относительно начального положения на величину x ролик R рычага r будет скользить по линейке L и займет положение R' , а так как рычаг r жестко скреплен с нитедержателем NN, то нить повернется на угол  и в параллакс наблюдаемой точки введется поправка . Из рис. 23 следует

(60)

Рассмотрим треугольник . Так как угол  небольшой, то этот треугольник можно считать прямоугольным с углом 90 при вершине R.

(61)

Отрезок RR' найдем из прямоугольного треугольника RR'Q

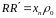
Подставим полученное значение в равенство (61)

(62)

Значение  подставим в выражение (60)

(63)

Корректор должен решать следующую формулу

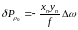(64)

Приравняем выражения (63) и (64) и решим относительно

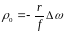(65)

Корректор

К орректор состоит из рычага r, скрепленного под прямым углом с правым нитедержателем NN(N'N') (рис. 23) и позволяет изменять угол между нитью и осью X стереометра. Этот угол сохраняется постоянным при движении общей каретки. Поправка в измеряемый параллакс будет .

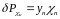(66)

Коррекционный механизм должен решать следующую формулу

(67)

Приравняв выражения (66) и (67), получим