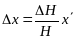- •1.Виды фототопографических съемок
- •2.Построение изображения идеальной оптической системой
- •Построение изображения идеальной оптической системой
- •3.Основные точки и плоскости оптической системы, Построение изображения наклонной плоскости
- •Построение изображения наклонной плоскости
- •4.Оптическое изображение пространства в фокальной плоскости объектива
- •7.Система координат аэроснимка, Элементы внутреннего ориентирования
- •Элементы внутреннего ориентирования
- •8. Элементы внешнего ориентирования
- •12.Центральная проекция аэроснимка, Основные элементы перспективы
- •Основные элементы перспективы
- •13.Построение перспектив отрезков прямых, параллельных линии направления съемки
- •14.Построение изображения прямой, лежащей под углом к линии направления съемки
- •15.Построение изображения прямой, расположенной перпендикулярно к линии направления съемки
- •16.Построение изображений вертикальных прямых
- •22.Масштаб наклонного снимка равнинной местности
- •23.Искажение направлений под влиянием наклона снимка
- •24.Смещение точек на аэроснимке под влиянием его угла наклона
- •25.Смещение точек на аэроснимке под влияние рельефа местности
- •26.Искажение направлений и углов на аэроснимке под влиянием рельефа местности
- •За вершину принята точка надира
- •За вершину направлений принята главная точка
- •27.Графическая фототриангуляция
- •Редуцирование - Процесс приведения сети фототриангуляции к заданному масштабу и ее ориентирование относительно геодезической системы координат.
- •28. Фотосхемы
- •29.Назначение и принцип трансформирования аэроснимков
- •Приравняем полученные выражения и решим их относительно
- •30.Трансформирование аэроснимков по зонам
- •Способы трансформирования снимков
- •31.Геометрические условия трансформирования
- •32. Совместное рассмотрение геометрических и оптических условий трансформирования. Оптические условия трансформирования - для получения резкого изображения на экране:
- •Согласование геометрических и оптических условий трансформирования
- •33.Универсальный топографический проектор утп-2 и трансформирование снимков на нём
- •34.Методика трансформирования снимков. Расчёт установочных величин
- •35. Монтирование фотопланов
- •36. Бинокулярное, монокулярное, стереоскопическое зрение и наблюдение снимков.
- •Стереоскопическое наблюдение снимков
- •37. Модель местности
- •38. Зависимость между продольными параллаксами и превышениями точек при идеальном случае съёмки.
- •39. Зависимости между координатами точки объекта и координатами ее изображения на одиночном снимке. Определение пространственных координат точек снимка.
- •Определение пространственных координат точек снимка
- •40. Определение направляющих косинусов
- •41. Определение координат точек снимка по соответствующим координатам точек объекта
- •42. Зависимость между координатами соответствующих точек горизонтального и наклонных снимков
- •43. Поправка за превышение правого конца базиса фотографирования
- •4 4. Связь между продольными параллаксами на горизонтальном и наклонном снимках
- •45. Уравнение ориентирования на стереометре
- •46. Теория коррекционных механизмов стереометра
- •47. Ориентирование снимков на стереометре
- •48. Определение элементов внешнего ориентирования снимка по опорным точкам
- •50. Допплеровское оборудование, гиростабилизирующая установка, определение угловых элементов ориентирвания.
- •51. Статоскоп, радиовысотомер
- •52. Аэрорадионивелирование.
- •53. Использование спутниковых систем для определения координат центров фотографирования. Ascot
41. Определение координат точек снимка по соответствующим координатам точек объекта
В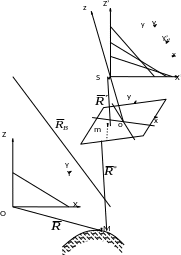 ектор
ектор
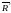 системе координат Sxyz
определяется координатами x,y,z=-f.
системе координат Sxyz
определяется координатами x,y,z=-f.
Вектор
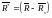 в этой же системе координат определяется
координатами X*,
У*, Z*,
а в системе координат SХ'У'Z'
в этой же системе координат определяется
координатами X*,
У*, Z*,
а в системе координат SХ'У'Z'
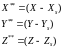
Запишем соотношение
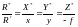
Решим равенство относительно х и у
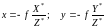
Координаты точки М измеряют в системе координат OXYZ. Чтобы перейти в систему координат Sxyz, необходимо применить формулы преобразования координат
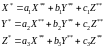
или
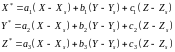 (20)
(20)
здесь ai, bi, ci - направляющие косинусы;
X, У, Z - координаты точки М в системе OXYZ;
Xs, Уs, Zs - координаты точки S в системе OXYZ.
С учетом (20) формулы (19) примут вид
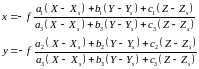
42. Зависимость между координатами соответствующих точек горизонтального и наклонных снимков
П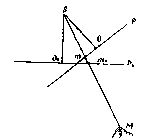 о
координатам точки m
измеренным на наклонном снимке, можно
найти координаты соответствующей точки
на горизонтальном снимке, если известны
угловые элементы внешнего ориентирования
наклонного снимка. Этот процесс называется
трансформированием координат.
о
координатам точки m
измеренным на наклонном снимке, можно
найти координаты соответствующей точки
на горизонтальном снимке, если известны
угловые элементы внешнего ориентирования
наклонного снимка. Этот процесс называется
трансформированием координат.
Пусть х0, у0, координаты изображения m0 точки M объекта на горизонтальном аэроснимке P0, полученном из точки фотографирования S, а x и у - координаты изображения той же точки местности на наклонном снимке Р, полученном из той же точки фотографирования S.
Используя основные формулы для горизонтального снимка можно написать следующие формулы для определения координат точки М
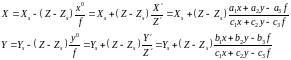 (25)
(25)
Решим полученные выражения относительно х0, у0, в результате получим формулы для определения координат горизонтального снимка х0, у0 если известны координаты наклонного снимка х, у.
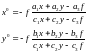 (26)
(26)
Формулы (26) строгие и их можно использовать при любых значениях угловых элементов внешнего ориентирования наклонного снимка.
с учетом только членов первого порядка малости
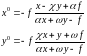 (27)
(27)
Выполним преобразования применительно к х0, для этого и числитель и знаменатель умножим на 1/f
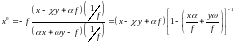 (28)
(28)
Из математики известно, что
(1-)-1=1++2+…, если - величина малая.
Ограничиваясь величинами первого порядка малости, будем иметь
(1-)-1=1+. ( 29 )
В
выражении (28)
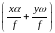 - величина малая, поэтому уравнение (28)
с учетом (29) будет иметь вид
- величина малая, поэтому уравнение (28)
с учетом (29) будет иметь вид
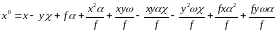 (30)
(30)
В
равенстве (30)
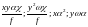 являются членами второго порядка
малости и ими можно пренебречь, тогда
являются членами второго порядка
малости и ими можно пренебречь, тогда
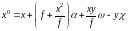 (31)
(31)
Аналогично получим формулу для координаты y0
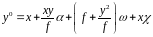
43. Поправка за превышение правого конца базиса фотографирования
П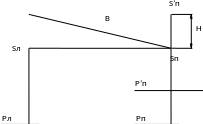 ри
идеальном случае съемки должны быть
горизонтальны не только снимки, но
и базис фотографирования. В действительности
базис фотографирования имеет наклон.
ри
идеальном случае съемки должны быть
горизонтальны не только снимки, но
и базис фотографирования. В действительности
базис фотографирования имеет наклон.
Найдем поправку в координаты точки правого аэроснимка за превышение правого конца базиса фотографирования. Спроектируем точку А местностина снимки Pп и P'п, получим точки а и а' .
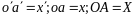
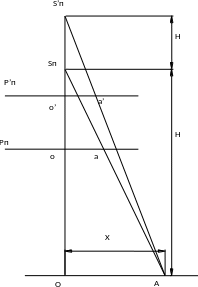
Из
подобия треугольников
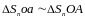 и
и
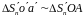 можно написать
можно написать
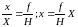 (33) и
(33) и
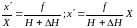 (34).
(34).
Поправка за превышение правого конца базиса фотографирования будет равна
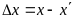
Подставим в равенство (35) выражения (33) и (34)
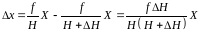 (36)
(36)
В
выражении (Зб)
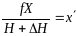 ,
на основании формулы (34), следовательно
,
на основании формулы (34), следовательно