38. Зависимость между продольными параллаксами и превышениями точек при идеальном случае съёмки.

Разность абсцисс соответс­твенных точек левого и правого снимков стереопары называется продольным параллаксом Р

,

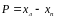а разность ординат этих же точек - поперечным параллак­сом q

.

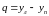Продольный параллакс Р точки А равен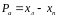 , или в соответствии с чертежом .

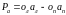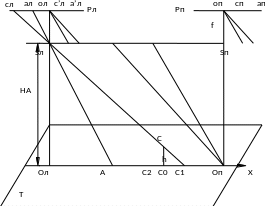
Из подобных треугольников 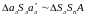получим

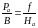
отсюда

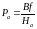
Из этого выражения следует, что продольный параллакс какой-либо точки равен базису фотографирования в масштабе этой точ­ки, т.е. и точки местности, расположенные в одной го­ризонтальной плоскости, имеют равные продольные параллаксы.

Возьмем точку С также лежащую на оси X, но имеющую превы­шение h над плоскостью Т. Точка С изобразится на аэросним­ках в точках c_л и с_п.

Перенесем абсциссу 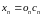на левый аэроснимок аналогично предыдущему, получим 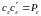. Из подобия треугольников

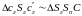
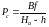
Найдем разность продольных параллаксов 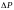точек С и А

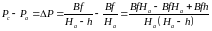
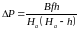
В этом выражении 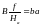, следовательно

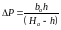
Зная разность продольных параллаксов P, можно вычислить превышение h, по формуле

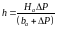
Выясним геометрическое значение разности продольных параллак­сов P. Для этого продолжим проектирующие лучи S_лС и S_пС до пересечения их с плоскостью Т. Получим точки С₁ и С₂ (рис. 10).

Из подобия треугольников 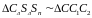можно записать

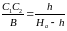
откуда

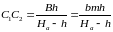
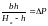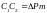В приведенной формуле , следовательно , т.е. 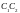- соответствует разности продольных параллаксов на местности (m - знаменатель масштаба снимков).

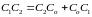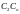В соответствии с чертежом ,где и 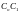- смещение точек за рельеф местности для правого и левого аэроснимков.

Следовательно, разность продольных параллаксов P - это сумма искажений абсцисс точки, вызванная рельефом местности.

39. Зависимости между координатами точки объекта и координатами ее изображения на одиночном снимке. Определение пространственных координат точек снимка.

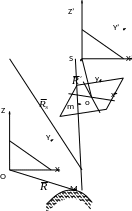
Векторы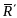 и 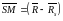коллинеарны,

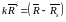(1)

где k - скаляр. Поделим обе части выражения на вектор

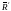
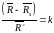(2)

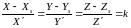(3)

Решим выражение ( 3 ) относительно X и Y

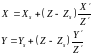(4)

Определение пространственных координат точек снимка

П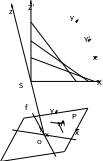 ространственные координаты Х', У', Z' точки снимка можно найти если известны плоские координату x ,у и направляющие косинусы.

M( x, y, z=-f.)

Используя в геометрии формулы

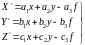(5)

Формулы (5) позволяют перейти от плоских координат точки сним­ка к пространственным. Формулы обратного перехода имеют вид

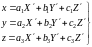(6)

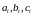- направляющие косинусы которые определяют взаимное положение двух систем координат SХ'У'Z' и Sxyz.( a_i - осью Х' с x,y,z;b_i - Y' с x,y,z;c_i )

В матричной форме зависимости (5) и (6) будут иметь вид

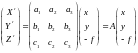
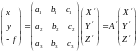Матрицы А и А' - матрицами преобразования координат.

40. Определение направляющих косинусов

В результате первого поворота вокруг оси У' на угол  система координат SХ'У'Z'

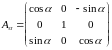Второй поворот выполним вокруг оси x' на угол , который преобразу­ет систему Sx'y'z' в Sx''y''z''.

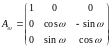
После третьего поворота вокруг оси z" на угол  система коор­динат Sx''y''z'' переходит в систему координат Sxyz.

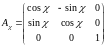
полученный ре­зультат подставим в равенство (10)

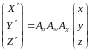
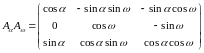
Если известны направляющие косинусы, то, как следует из зави­симостей (16), утлы , ,  можно найти по формулам

.

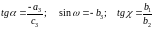Угловые элементы внешнего ориентирования планового снимка -величины малые, поэтому можно разложить в ряды тригонометричес­кие функции углов , , , входящих в формулы (16), и получить более простые выражения для определения направляющих косинусов планового снимка.