8. Векторное поле. Формулы Стокса и Остроградского -Гаусса.

58. Понятие линейного оператора. Матрица линейного оператора. Действия над линейными операторами.

1. Определение линейного оператора. Пусть V и W — линейные пространства, размерности которых равны соответственно n и m. Мы будем называть оператором А, действующим из V в W, отображение вида А: V —> W, сопоставляющее каждому элементу х пространства V некоторый элемент у пространства W. При этом будем использовать обозначение у = А (х) или у = Ах.  Определение. Оператор А, действующий из V в W, называется линейным, если для любых элементов x₁ u x₂ пространства V и любого комплексного числа λ выполняются соотношения:  1°. λ( x₁ + x₂) = λx₁+ λx₂ (свойство аддитивности оператора);  2°. А (λх) = λАх (свойство однородности оператора).  Замечание. Если пространство W совпадает с пространством V, то линейный оператор, действующий в этом случае из V в V, называют также линейным преобразованием пространства V.  2. Действия над линейными операторам. Пространство линейных операторов. В множестве всех линейных операторов, действующих из V в W, определим операции суммы таких операторов и умножения оператора на скаляр.  Пусть А и В — два линейных оператора, действующих из V в W. Суммой этих операторов назовем линейный оператор А + В, определяемый равенством

 (А + В)х = Ах + Вх.           (5.1)

Произведением линейного оператора А на скаляр λ назовем линейный оператор λА, определяемый равенством

(λА)х= λ(Ах).     (5.2)

Назовем нулевым оператор, обозначаемый символом О и отображающий все элементы пространства V в нулевой элемент пространства W.  Иными словами, оператор О действует по правилу Ох = 0.  Для каждого оператора А определим противоположный оператор  -А посредством соотношения

-А = (-1)А.

Легко проверить справедливость следующего утверждения.  Множество L(V, W) всех линейных операторов, действующих из V в W, с указанными выше операциями суммы и умножения на скаляр и выбранными нулевым оператором и противоположным оператором образует линейное пространство.  3. Свойства множества L (V, V) линейных операторов. Исследуем подробнее линейные операторы, действующие из V в V, т. е. изучим подробнее множество L(V, V).  Назовем тождественным (или единичным) оператором линейный оператор I, действующий по правилу Iх = х (здесь х — любой элемент V).  Введем понятие произведения линейных операторов из множества L(V, V).  Произведением операторов А и В из L(V, V) называется оператор АВ, действующий по правилу

(АВ)х = А(Вх).          (5.3)

Отметим, что, вообще говоря, АВ ≠ ВА.  Справедливы следующие свойства линейных операторов из L(V, V):  1°. λ(АВ) = (λА)В;  2°. (А + В)С = АС + ВС;  3°. А(В + С) = АВ + АС;  4°. (АВ)С = А(ВС).  Первое из свойств 1°-4° следует из определения произведения линейного оператора на скаляр (см. 5.2)) и определения произведения операторов (см. 5.3)).  Нам понадобится понятие обратного оператора для данного оператора А из L(V, V).  Определение 1. Линейный оператор В из L(V, V) называется обратным для оператора А из L(V, V), если выполняется соотношение  АВ = ВА = I.  Обратный оператор для оператора А обычно обозначается символом А^-1.  Из определения обратного оператора А следует, что для любого х Є V справедливо соотношение А^-1Ах = х.  Таким образом, если А^-1Ах = 0, то х = 0, т.е. если оператор А имеет обратный, то из условия Ах = 0 следует, что х = 0.  Мы будем говорить, что линейный оператор А действует взаимно однозначно из V в V, если любым двум различным элементам x₁ и x₂ отвечают различные элементы y₁ = Ax₁ и у₂ = Аx₂.  Если оператор А действует взаимно однозначно из V в V, то отображение А: V —> V представляет собой отображение V на V, т. е. каждый элемент у Є  V представляет собой образ некоторого элемента x Є V:

y = Ах. Отметим следующее утверждение.  Для того чтобы линейный оператор А из L(V, V) имел обратный, необходимо и достаточно, чтобы этот оператор действовал взаимно однозначно из V в V.  Определение 2. Ядром линейного оператора А называется множество всех тех элементов х пространства V, для которых Ах = 0. Ядро линейного оператора А обозначается символом ker А.  Если ker A = 0, то оператор А действует взаимно однозначно из V в V..  Определение 3. Образом линейного оператора А называется множество всех элементов у пространства V, представимых в виде     у = Ах. Образ линейного оператора А обозначается символом im A (Символ im следует отличать от символа Im, используемого для обозначения мнимой части комплексного числа).  Замечание 2. Отметим, что если ker А = 0, то im A = V, и наоборот. Поэтому наряду с отмеченным выше условием ker A = 0 условие im A = V также является необходимым и достаточным для того, чтобы оператор А имел обратный.  Замечание 3. Очевидно, ядро ker А и образ im A — линейные подпространства пространства V. Поэтому можно рассматривать размерности dim (ker А) и dim (imA) этих подпространств.  Справедлива следующая теорема.  Теорема 5.1. Пусть размерность dimV пространства V равна n, и пусть А — линейный оператор из L(V, V). Тогда

dim (im А) + dim (ker A) = n.

1. Матрицы линейных операторов в заданном базисе линейного пространства V. Фиксируем в линейном пространстве V базис  e₁, е₂,..., е_n. Пусть х — произвольный элемент V и

разложение х по данному базису.  Пусть А — линейный оператор из L(V, V). Тогда из (5.11) получаем 

Полагая 

перепишем (5.12) в следующей форме: 

Рассмотрим квадратную матрицу А с элементами а^j_k:

А = (а^j_k).

Эта матрица называемся матрицей линейного оператора в заданном базисе е₁, е₂,..., е_n.  Наряду с ранее указанным способом записи линейного оператора используется при заданном базисе e₁, е₂,...,е_n матричная форма записи: у = Ах.  Замечание 1. Если оператор А нулевой, то все элементы матрицы А этого оператора равны нулю в любом базисе, т.е. А — нулевая матрица.  Замечание 2. Если оператор А единичный, т. е. А = I, то матрица этого оператора будет единичной в любом базисе. Иными словами, в этом случае А = Е, где Е — единичная матрица. В дальнейшем единичную матрицу мы будем обозначать также символом I.  Мы выяснили, что каждому линейному оператору А из L(V, V) при заданном базисе линейного пространства V отвечает матрица А этого оператора. Теорема 5.5. Пусть в линейном пространстве V задан базис е₁, е₂,..., е_n, и пусть А = (а^j_k) — квадратная матрица, содержащая n строк и n столбцов. Существует единственный линейный оператор А, матрицей которого в заданном базисе является матрица А.  Теорема 5.6. Ранг линейного оператора А равен рангу матрицы А этого оператора: rang A = rang A. 

Линейный оператор и его матрица. Переход к другому базису

Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n  и пусть e₁,  e₂, ..., e_n - базис в X. Обозначим через A e₁ = (a₁₁,...,a_n1), ... , A e_n = (a_1n,...,a_nn) образы базисных векторов e₁,  e₂, ..., e_n .

Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно   каждая  квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения

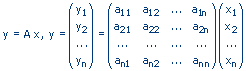
с одной стороны, связывают координаты образа y = A x с координатами прообраза X, с другой стороны,  описывают действие оператора, заданного матрицей A.

При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве X произошел переход от базиса e = {e₁, ... , e_n}  к базису e' = {e'₁, ... , e'_n} . Связь между матрицей A_e  оператора A в базисе e  и матрицей A_e'  этого оператора в базисе e' задается формулой 

Здесь    -  матрица перехода от базиса e к базису  e' и обратная к ней.