6. Поверхностный интеграл 1-го рода.

Задача, приводящие к понятию поверхностного интеграла Задача о массе поверхности. Требуется найти массу материальной поверхности  , на которой распределена масса с плотностью  .

Разобьем поверхность сетью дуг на   элементарных частей, площади каждой из которых равны  , а диаметр  . Выберем в каждой из них точку  , будем считать, что плотность каждой части постоянна и равна  . Тогда массу каждой элементарной части можно считать равной  . Сумма всех таких произведений приближенно выражает массу всей заданной материальной поверхности  . Будем увеличивать число разбиений так, чтобы наибольший из диаметров областей   стремился к нулю. Тогда массу материальной поверхности можно найти по формуле 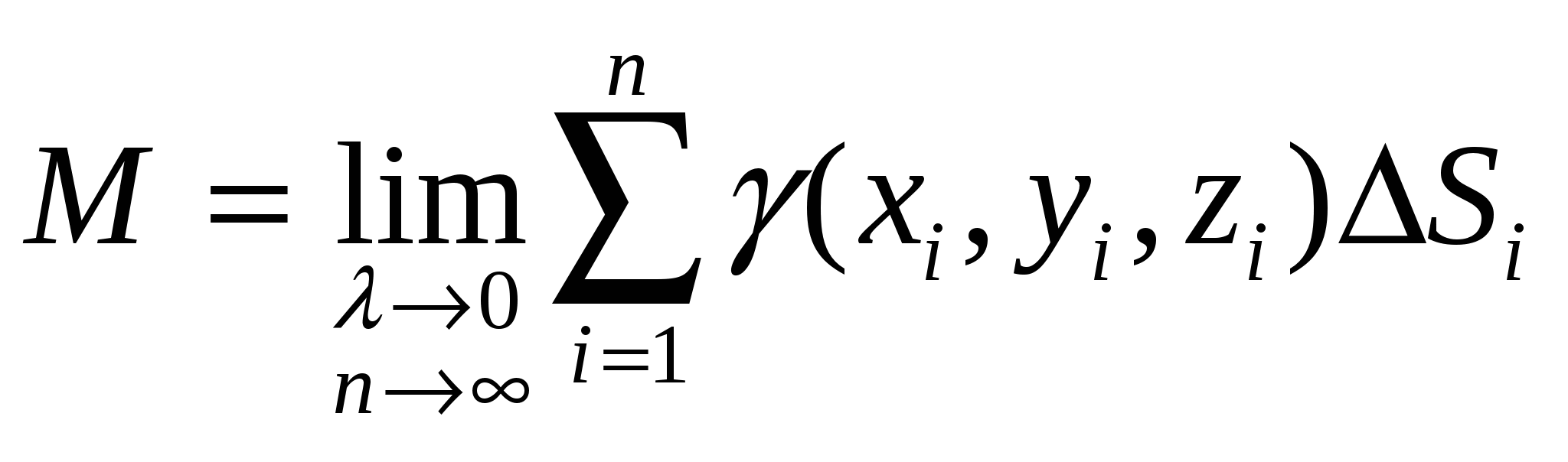 . Понятие поверхностного интеграла Пусть дана некоторая поверхность  , в точках которой определена непрерывная функция  . Разобьем поверхность на   частей площадью   и с диаметром  . В каждой из частей выберем произвольную точку  . Составим сумму  . Будем увеличивать число точек разбиения таким образом, чтобы наибольший из диаметров частичных областей   стремился к нулю.  Определение 1. Поверхностным интегралом первого рода от функции   по поверхности   называется предел интегральной суммы   при   ( ), независящий ни от способа разбиения поверхности на части, ни от выбора точек  . Обозначается  . Теорема 1. Если поверхность   гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция   непрерывна на этой поверхности, то поверхностный интеграл существует. Основные свойства интеграла первого рода Основные свойства поверхностного интеграла первого рода.

1. .

2. .

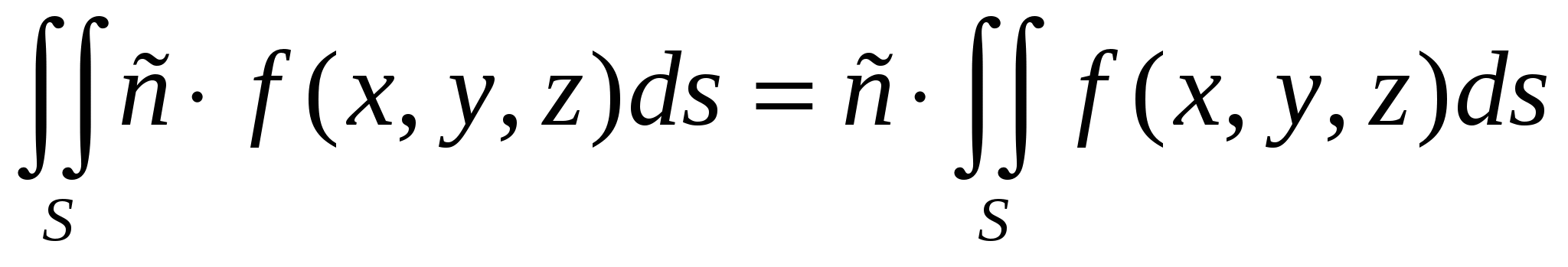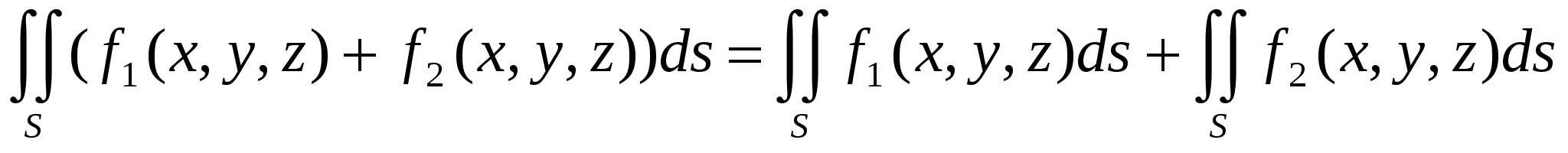Следствие 1. Имеется в виду алгебраическая сумма функций. Следствие 2. Данное свойство справедливо для любого конечного числа функций.

3. Если поверхность   разбить на части   и 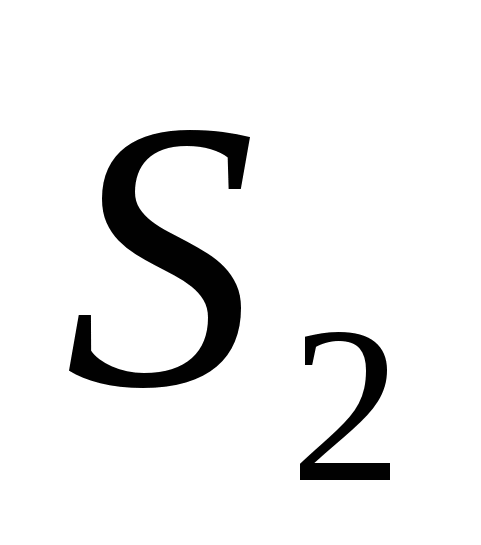  такие, что 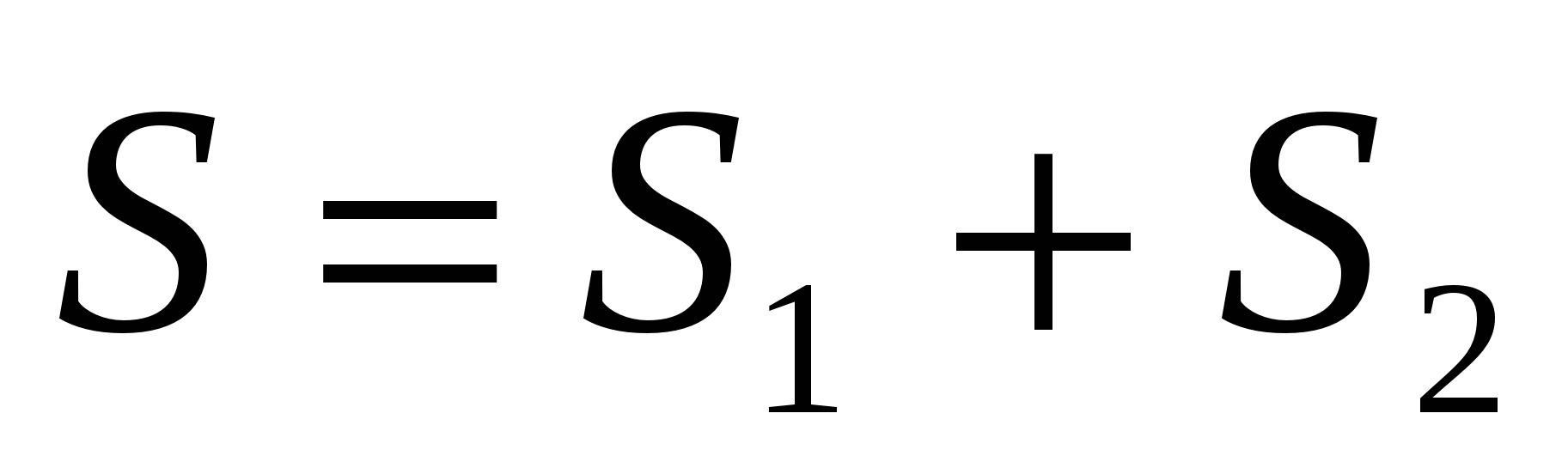 ,а пересечение   и   состоит лишь из границы, их разделяющей, то

.

4. Если на поверхности   выполняется неравенство 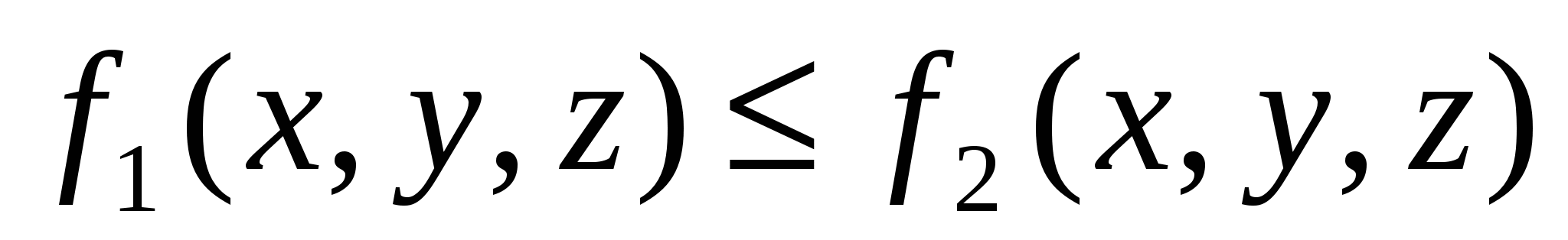 , то  .

5. .

6. .

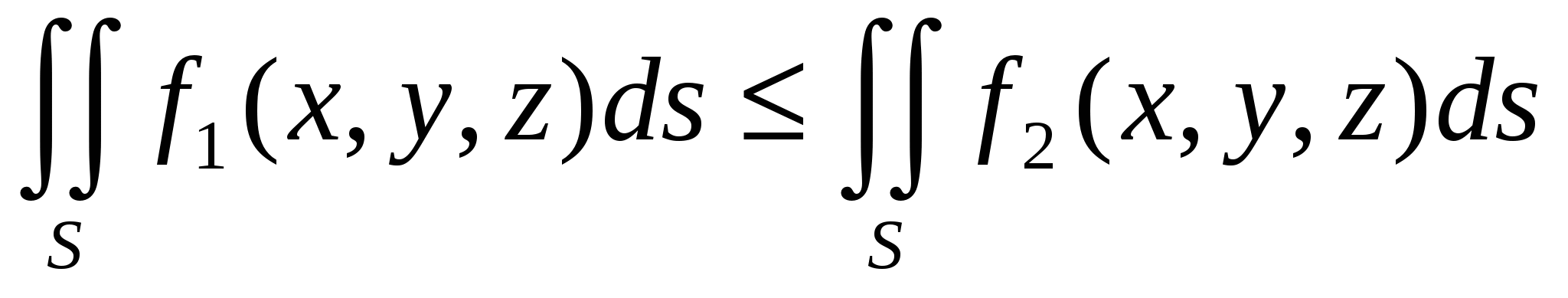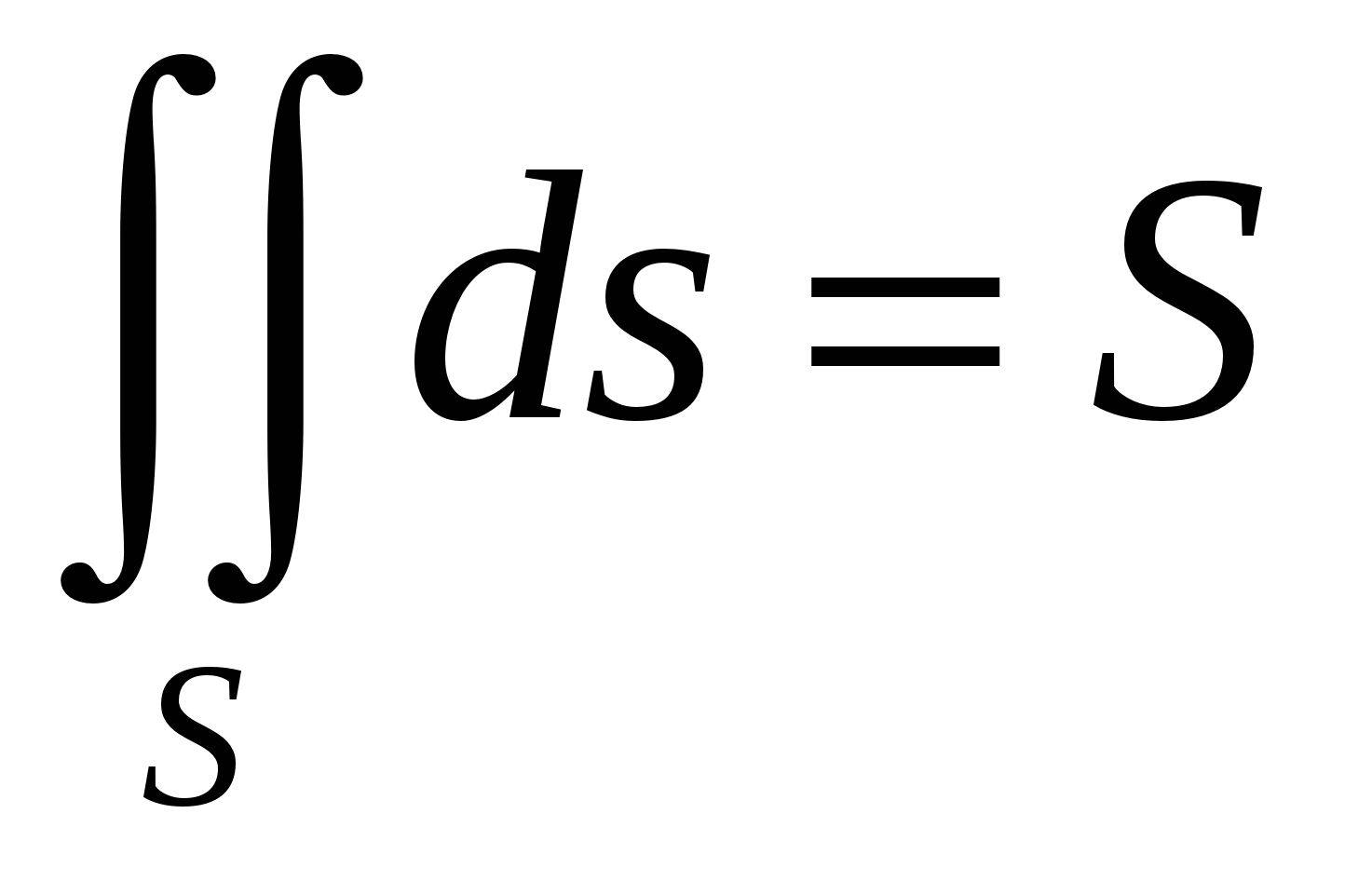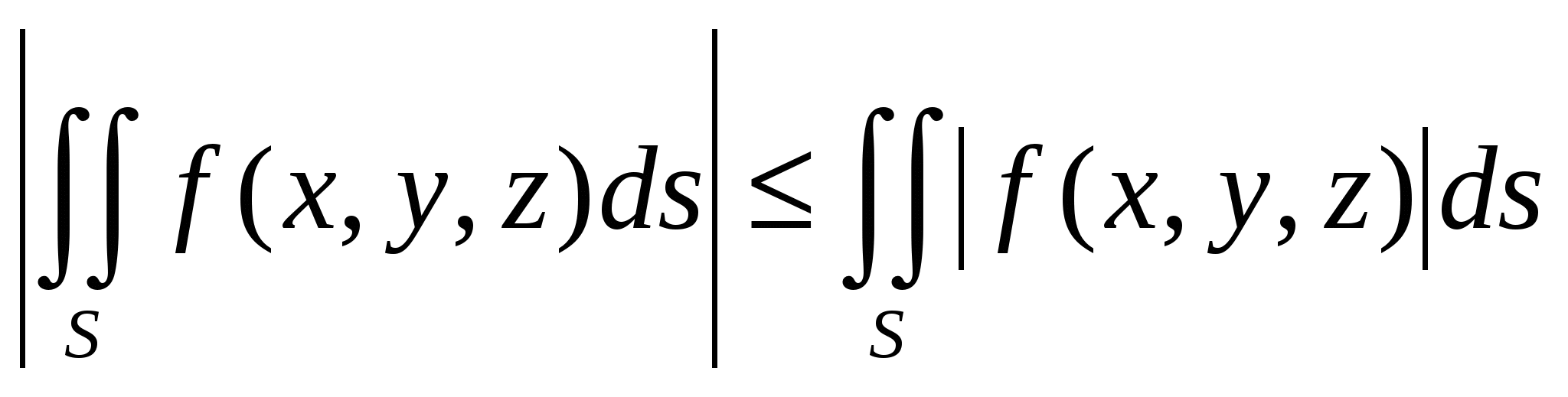7. (Теорема о среднем). Если   непрерывна на  , то на ней существует точка 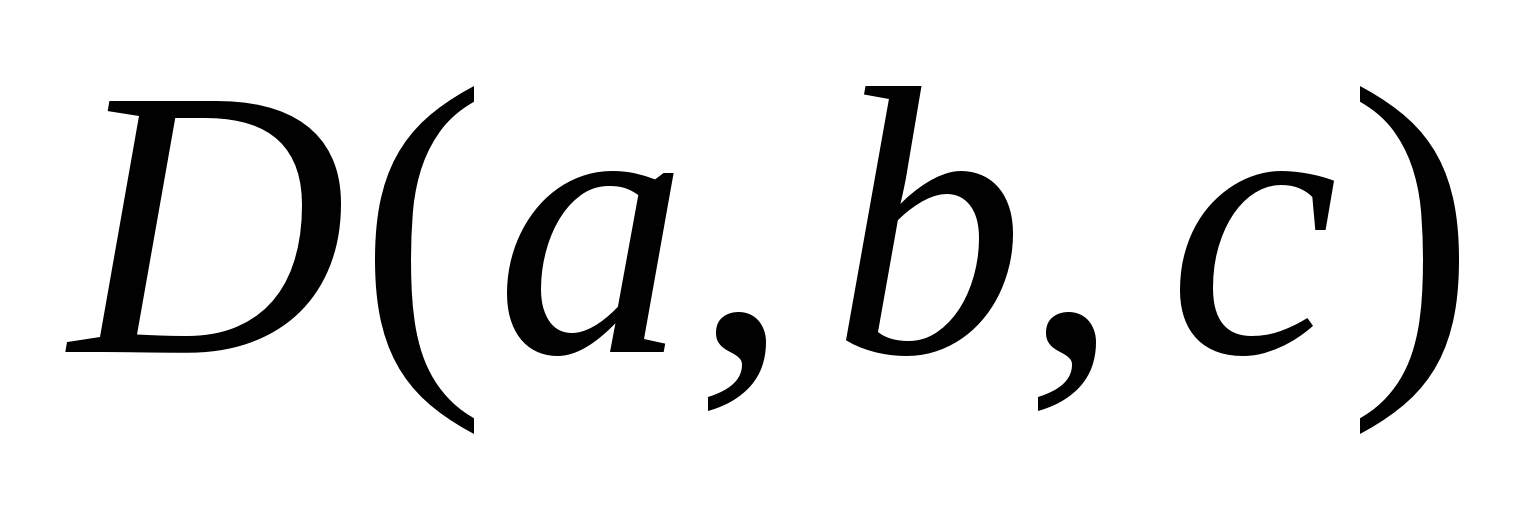  такая, что  .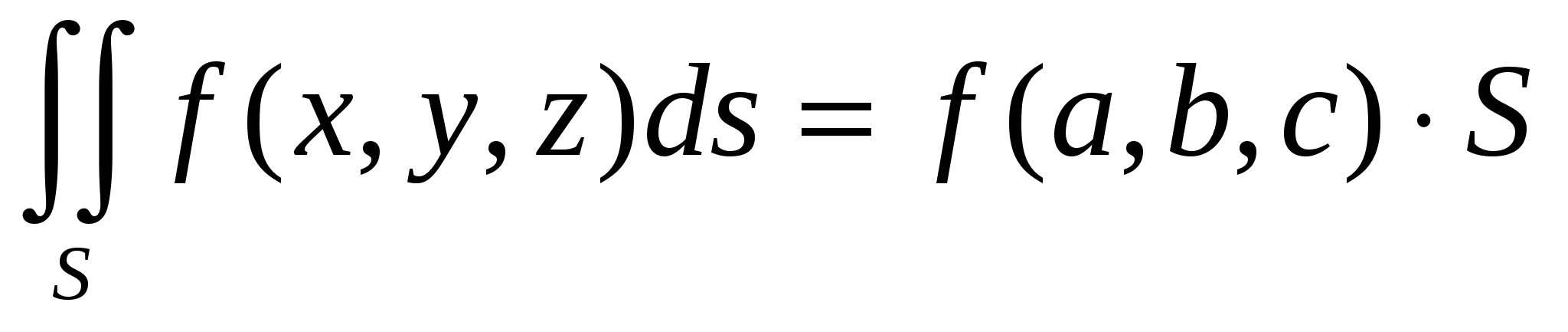

Вычисление поверхностного интеграла первого рода Пусть поверхность   задана уравнением вида  , тогда поверхностный интеграл можно вычислить по формуле: ,  где   – проекция   на плоскость  . Если поверхность   задана   или  , то формулы принимают вид: ,  , где   и   – проекции   на плоскости   и   соответственно. Приложения поверхностного интеграла первого рода Площадь поверхности. Пусть поверхность   задана уравнением  , ее проекция на плоскость   есть область  . Тогда площадь поверхности вычисляется по формуле  . Масса поверхности. Плотность распределения массы поверхности   задана функцией  . Масса поверхности вычисляется по формуле  .  Статистические моменты. Статистические моменты поверхности   с плотностью   находятся по формулам ,  ,  . Координаты центра тяжести. Координаты центра тяжести поверхности   с плотностью   находятся по формулам ,  ,  . Моменты инерции. Моменты инерции материальной поверхности   с плотностью   находятся по формулам ,  ,  ,