Диаметр вала не первом участке
d1≥
=65,5
мм
Принимаем d1 = 70 мм.
Диаметр вала на втором участке
d2≥
=51,9
мм
Принимаем d2 = 55 мм.
Диаметр вала на третьем участке
d3≥
=38,3
мм
Принимаем d3 = 40 мм.
Эскиз ступенчатого вала в масштабе показан на рисунке 4.
4.Вычислим полярные моменты инерции отдельных сечений вала:
Ір1=π·d14 / 32=π·(7,0·10-2)4/32=235,5·10-8 м4,
Ір2=π·d24 / 32=π·(5,5·10-2)4/32=89,7·10-8 м4,
Ір3=π·d34 / 32=π·(4,0·10-2)4/32=25,1·10-8 м4
5.Определим углы закручивания соответствующих участков вала:
φ0AB=[T1·ℓ1/(G·Ιp1)]·1800/π=[2076·12·10-2/(8·1010·235,5 ·10-8)]·1800/π=0,0760,
φ0BС=[T2·ℓ2/(G·Ιp2)]·1800/π=[1038·18·10-2/(8·1010·89,7 ·10-8)]·1800/π=0,1490,
φ0СD=[T3·ℓ3/(G·Ιp3)]·1800/π=[415·10·10-2/(8·1010·25,1 ·10-8)]·1800/π=0,1180
6.Определим полный угол закручивания вала:
φ0= φ0AB+ φ0BС+ φ0СD=0,0760+0,1490+0,1180=0,3430
Эпюра полного угла закручивания вала показана на рисунке 4.
Пятую задачу следует решать после изучения темы 2.5.Изгиб.
Краткие теоретические сведения
Тема 2.5. Изгиб
Изгиб – такой вид деформации бруса, при котором в его поперечных сечениях возникают изгибающие моменты.
Если одновременно с изгибающими моментами возникают и поперечные силы, то изгиб называют поперечным; если поперечные силы не возникают, то изгиб называют чистым.
С геометрической точки зрения изгиб характеризуется тем, что ось бруса, прямолинейная до деформации, при изгибе становится криволинейной (изогнутой).
Деформация изгиба возникает при нагружении бруса силами, действующими в плоскостях, проходящих через его продольную ось, и перпендикулярными этой оси, и парами сил, действующими в тех же плоскостях.
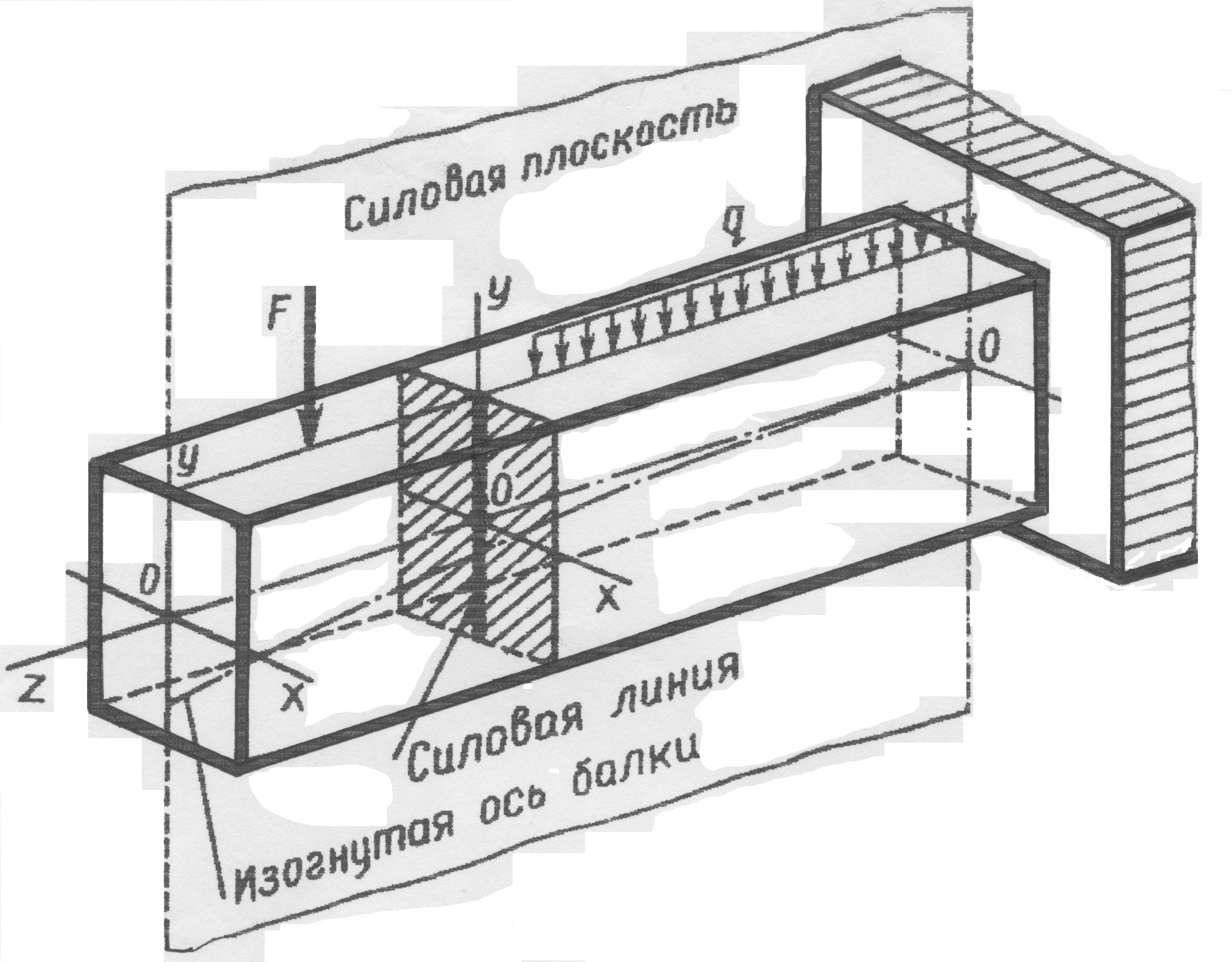
Ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения.
Плоскость, проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения называется главной плоскостью бруса.
В случае если силовая плоскость (плоскость действия нагрузок) совпадает с одной из главных плоскостей, имеет место прямой изгиб бруса, если не совпадает – косой изгиб.
В курсе сопротивления материалов будем рассматривать прямой изгиб.
Силовая линия – линия пересечения силовой плоскости с плоскостью поперечного сечения бруса.
Брусья, работающие на изгиб, называются балками.
Поперечные силы и изгибающие моменты
Поперечная сила Qу в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, приложенных к его отсеченной части.
Изгибающий момент Мх в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсеченной части, относительно той точки продольной оси бруса, через которую проходит рассматриваемое сечение.
Правило знаков для поперечной силы.
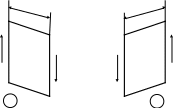а)
dz
б) dz
Qy Qy
Qy Qy
+ -
Силам, проворачивающим отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки, приписывается знак плюс, а силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения против хода часовой стрелки, приписывается знак минус.
Правило знаков для изгибающих моментов.
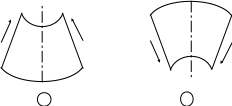
а) б)
Мх Мх
Мх Мх
+ -
Изгибающий момент считается приложенным, если элемент бруса изгибается выпуклостью вниз, т.е. таким образом, что его сжатые волокна находятся в верхней части.
Изгибающий момент считается отрицательным, если элемент бруса изгибается выпуклостью вверх, т.е. таким образом, что его растянутые волокна находятся в верхней части.
График, показывающий закон изменения поперечных сил по всей длине бруса, называется эпюрой поперечных сил.
График, показывающий закон изменения изгибающих моментов по всей длине балки, называется эпюрой изгибающих моментов.