Краткие теоретические сведения

Тема 2.4. Кручение; срез с кручением

Кручение – такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент Т.

Деформация кручения возникает при нагружении бруса парами сил, плоскости действия которых перпендикулярны его продольной оси. Моменты этих пар называют скручивающими моментами (Т_е).

Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, то есть брус находится в равновесии.

Крутящий момент, возникающий в произвольном поперечном сечении бруса, определяется с помощью метода сечений. Он численно равен алгебраической сумме скручивающих моментов, приложенных к оставленной части.

Знак крутящего момента не имеет физического смысла, но для определённости при построении эпюр условимся о следующем правиле знаков:

Считаем крутящий момент положительным, если для наблюдателя, смотрящего на проведённое сечение, он представляется направленным по часовой стрелке и отрицательным, если против часовой стрелки.

График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов.

При кручении бруса в поперечных сечениях возникают касательные напряжения.

Формула для определения касательных напряжений:

,

где Т – крутящий момент;

Wp – полярный момент сопротивления сечения, который является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении (м³; см³; мм³).

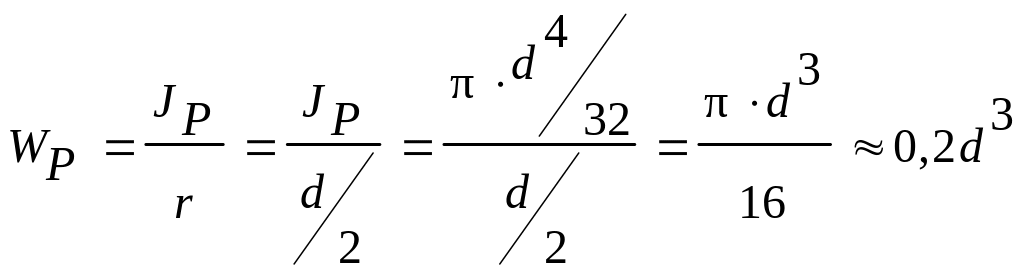
Угол закручивания

Деформация бруса при кручении характеризуется углом взаимного поворота двух сечений (углом закручивания). Полный угол закручивания бруса длиной ℓ определяется по формуле:

,

Произведение условно называют жёсткостью сечения круглого бруса при кручении.

Расчёты на прочность при кручении

Условие прочности при кручении имеет вид:

,

где - наибольшее касательное напряжение в опасном поперечном сечении бруса.

Существует 3 вида расчётов на прочность.

1. Проверочный

2. Проектный

При Wp=0,2d³

3. Определение допускаемого крутящего момента

Расчёт на жёсткость при кручении

За меру жёсткости при кручении принимают относительный (погонный) угол закручивания (угол закручивания на единицу длины) φ.

Условие жёсткости при кручении имеет вид:

где =(0,25...1) град/м.

Допускаемый угол закручивания зависит от назначения вала.

Существует 3 вида расчётов на жёсткость:

1. Проверочный

2. Проектный

,

,

3. Определение допускаемого крутящего момента

Из двух значений диаметра вала, определённых из расчётов на прочность и жёсткость, в качестве окончательного должен быть принят больший.

Алгоритм решения задачи №4

1. Определите значения скручивающих моментов ( подводимого к шкиву 1 и сни-

маемых со шкивов 2, 3, 4).

2. Постройте эпюры крутящих моментов.

3. Определите диаметры каждого участка ступенчатого вала из условия прочности.

Окончательно принимаемые значения должны быть округлены до ближайших стандартных по ГОСТ 6636-69.

4. Вычертите в масштабе эскиз ступенчатого вала.

5. Построите эпюру углов поворота сечения относительно левого торца вала.

6. Определите полный угол закручивания.

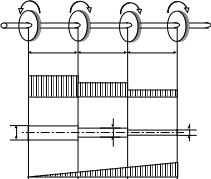
Пример 4. На ступенчатом валу (рис. 5) жестко закреплены четыре шестерни.

Мощность на ведомых шестернях Р₂=25кВт, Р₃=15кВт, Р₄=10кВт; частота вращения ведущей шестерни n=230мин^-1; допускаемое касательное напряжение τ_adm=37 МПа; расстояние между шестернями ℓ₁=120мм, ℓ₂=180мм, ℓ₃=100мм; модуль упругости G=8·10¹⁰Па.

Требуется построить эпюру крутящих моментов ступеней вала и полный угол закручивания с построением эпюры углов поворота сечений относительно левого торца вала.

Те₁ Те₂ Те₃ Те₄

ℓ₁ ℓ₂ ℓ₃

2076 1038 415

Эпюра «Т»(Н·м)

^{0 0}

d₂ d₃

d₁

Эпюра «φ» (град) 0,076 0,225

0,343

Рисунок 4 – Ступенчатый вал

1.Определим скручивающие моменты по формуле:

Т_е=9,55·P/n,

Т_е2=9,55·25·10³/230=1038 Н·м,

Т_е3=9,55·15·10³/230=623 Н·м,

Т_е4=9,55·10·10³/230=415 Н·м,

Т_е1=Т_е2+ Т_е3+ Т_е4,

Т_е1=1038+623+415=2076 Н·м

2.Для построения эпюры крутящих моментов определяем величины крутящих моментов на каждом участке вала. Для этого воспользуемся правилом: крутящий момент в любом сечении вала численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от выбранного сечения. Рассмотрим действие внешних моментов слева от сечения.

В сечении 1-1 Т₁ = Т_е1 = 2076 Н·м,

в сечении 2-2 Т₂ = Т_е1 – Т_е2 = 2076 – 1038 = 1038 Н·м,

в сечении 3-3 Т₃ = Т_е1 – Т_е2 – Т_е3 = 2076 – 1038 – 623 = 415 Н·м

Эпюра крутящих моментов для вала показана на рисунке 4.

3.Определим диаметры вала на каждом участке из условия прочности на кручение по

формуле:

d ≥ )