Краткие теоретические сведения

Тема 1.1.2.2. Системы произвольно расположенных сил

1. Плоская система произвольно расположенных сил

Система сил, линии действия которой лежат в одной плоскости и расположены произвольным образом, называется плоской системой произвольно расположенных сил.

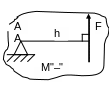
Моментом силы относительно точки называется взятое со знаком «+» или «-» произведение модуля силы на перпендикуляр, опущенный из точки на линию действия силы, который называют плечом силы.

Единицы измерения момента силы - Н·м, кН·м.

Точка, относительно которой берётся момент, называется центром момента.

	Правило знаков для двух моментов Момент силы положителен, если сила стремится вращать плечо вокруг центра моментов по часовой стрелке и отрицателен, если против часовой стрелки.
Пример: Определите моменты сил относительно точки А. М1=F∙h1, М2=0, М3=–F∙h3 Если линия действия силы проходит через точку, то момент силы относительно этой точки равен 0.

Условие равновесия плоской системы произвольно расположенных сил

Плоская система произвольно расположенных сил находится в равновесии, когда главный вектор и главный момент равны нулю.

Уравнения равновесия плоской системы произвольно расположенных сил

Уравнения равновесия плоской системы произвольно расположенных сил могут быть представлены в трёх формах:

Алгебраические суммы моментов всех сил относительно трёх любых, но не лежащих на одно прямой точек, должны быть равны 0.

Ось Х не должна быть перпендикулярна к прямой, проходящей через точки А и В.

Классификация нагрузок

1. По способу приложения:

- сосредоточенные (приложенные в точке) – F;

- распределённые (могут быть распределены по длине, по площади, по объёму) – Q=q·ℓ

F

q

Q=qℓ

ℓ/2

ℓ

q – интенсивность распределённой нагрузки, т.е. сила, приходящаяся на единицу длины участка (единицу площади, единицу объёма); единицы измерения - кН/м.

2. По характеру действия:

-статические, т.е. возрастающие от 0 до конкретного значения, а затем остающиеся постоянными;

-динамические (ударные) – прикладываются сразу с максимальной величиной;

-повторно-переменные – повторяются через определённый промежуток времени.

3. По времени действия:

-постоянные;

-временные.

2. Пространственная система произвольно расположенных сил

Моментом силы F относительно оси Z называется момент проекции F_π этой силы на плоскость π, перпендикулярную оси моментов, относительно точки О их пересечения.

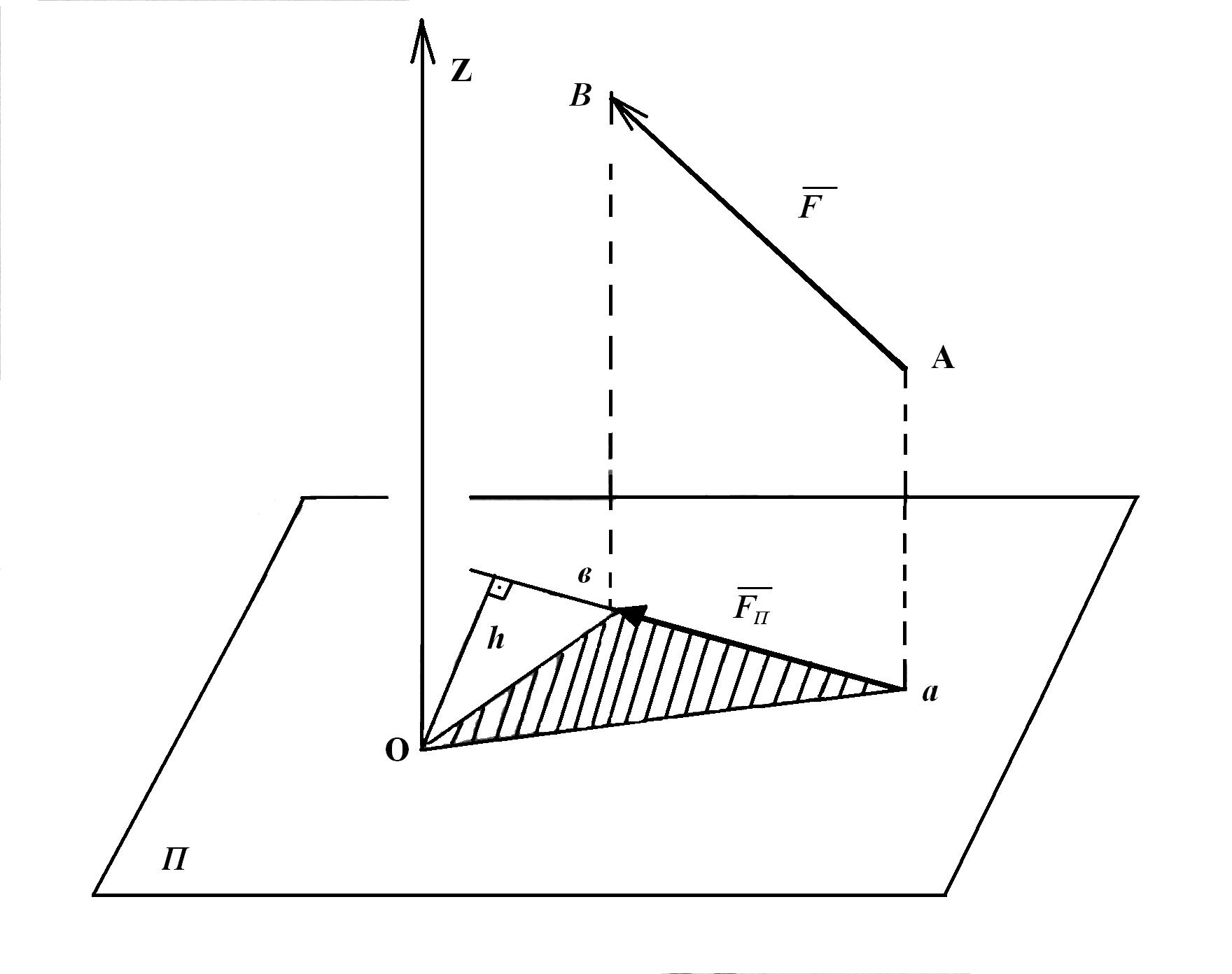
Если сила пересекает ось или параллельна оси, то эта сила момента относительно оси не даёт.

Для вычисления момента силы относительно оси рекомендуется разложить силу на три взаимно перпендикулярные составляющие, параллельные осям координат.