Задание 9

3. Получить механическую выборку из данных, приведенных в задании 7, отобрав 25 значений (каждое второе, считая в порядке записи сверху вниз по колонкам и по этой выборке). Используя критерий согласия Пирсона, проверить согласие выборочных значений с гипотезой о нормальном распределении генеральной совокупности с параметрами, оцененными предварительно по выборке.

Решение:

Выдвинем гипотезу Н0: F_X(x)=F₀(х), где F₀(х) – функция нормального распределения с параметрами, полученными по выборке в № 8.3 (а=34,6765; 9,5281). Для этого определим в таблице величину расчетного коэффициента Пирсона по итогам таблицы 9.1.

Для расчета теоретических частот вычислим значения p_i по формуле (совокупность разбита на 5 групп с шагом ):

значения функции находим по таблицам распределения интеграла вероятности.

Для 1-ого интервала

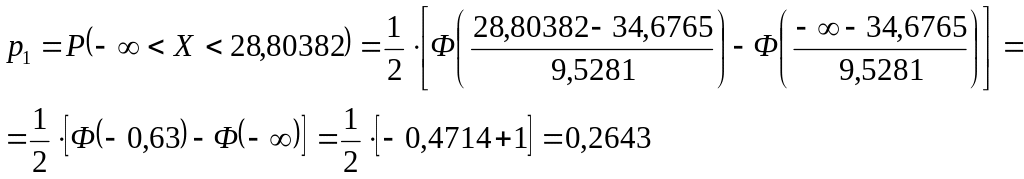
Теоретическая частота и т.д.

Таблица 9.1.

Расчет критерия Пирсона

№ п/п	Интервал	Частота, m_i	p_i	Теоретическая частота,
1	– 28,80382	10	0,2643	7	3	9	1,285714
2	28,80382– 33,95474	5	0,2038	5	0	0	0
3	33,95474– 39,10566	0	0,2127	5	-5	25	5
4	39,10566– 44,25658	2	0,1677	4	-2	4	1
5	44,25658–	8	0,1515	4	4	16	4
Итого		25	1	25			11,28571

Значение Пирсона определим по формуле:

; при уровне значимости α=0,01 и числе степеней свободы v=5 – 2 – 1=2 находим . Так как 11,286>9,2, то гипотеза о нормальном распределении отвергается.

Задание 10

Получить две механические выборки, объемом по 25 значений, из данных, приведенных в задании 7, включая в первую значения, стоящие на нечетных местах, а во вторую – на четных (нумерация производится по колонкам).

Найти выборочное уравнение линейной регрессии Y на Х по результатам двух выборок, считая первую выборку значениями X ,а вторую – Y. Проверить гипотезу о значимости коэффициента корреляции.

Решение:

Получим две механические выборки, запишем их в таблицу 9.1 и определим итоговые и средние показатели, необходимые для расчета коэффициентов корреляции и регрессии.

Таблица 9.1.

Определение коэффициентов корреляции и регрессии

№ п/п							·
1	45,7985	47,2978	10,7627	12,6213	115,8347	159,2977	135,8389
2	48,5226	48,7486	13,4868	14,0721	181,8925	198,0246	189,7872
3	44,3587	43,2306	9,3229	8,5541	86,9156	73,1730	79,7488
4	44,4744	46,7948	9,4386	12,1183	89,0863	146,8537	114,3794
5	47,9989	45,6923	12,9631	11,0158	168,0407	121,3483	142,7986
6	43,6532	49,4075	8,6174	14,7310	74,2588	217,0030	126,9424
7	45,8035	44,9188	10,7677	10,2423	115,9423	104,9051	110,2857
8	45,3773	45,3216	10,3415	10,6451	106,9456	113,3186	110,0860
9	48,7622	40,6574	13,7264	5,9809	188,4127	35,7714	82,0962
10	47,0493	45,5494	12,0135	10,8729	144,3230	118,2204	130,6213
11	27,4098	28,6561	-7,6260	-6,0204	58,1566	36,2450	45,9117
12	24,4059	27,5624	-10,6299	-7,1141	112,9958	50,6101	75,6223
13	28,9174	26,6193	-6,1184	-8,0572	37,4354	64,9181	49,2974
14	25,9613	27,0814	-9,0745	-7,5951	82,3474	57,6852	68,9219
15	28,8153	25,1591	-6,2205	-9,5174	38,6952	90,5805	59,2033
16	29,1856	30,2499	-5,8502	-4,4266	34,2254	19,5946	25,8966
17	30,9916	29,3445	-4,0442	-5,3320	16,3559	28,4300	21,5638
18	29,9391	23,6529	-5,0967	-11,0236	25,9768	121,5193	56,1844
19	27,1893	24,8246	-7,8465	-9,8519	61,5683	97,0595	77,3032
20	29,3138	29,6166	-5,7220	-5,0599	32,7418	25,6024	28,9529
21	30,7951	25,0384	-4,2407	-9,6381	17,9839	92,8926	40,8727
22	23,8167	24,7476	-11,2191	-9,9289	125,8693	98,5827	111,3936
23	23,3705	30,4135	-11,6653	-4,2630	136,0803	18,1730	49,7291
24	24,2096	29,6136	-10,8262	-5,0629	117,2076	25,6328	54,8120
25	29,7766	26,7133	-5,2592	-7,9632	27,6597	63,4122	41,8803
Итого	875,8962	866,912			2196,9519	2178,8538	2030,1299
В среднем	35,03585	34,67648			9,3743	9,3356	84,5887