Расчетная часть
1. Метод Каплана - Майера
На испытание было поставлено N = 40 элементов. Моменты отказов элементов представлены в табл.1. Все элементы работали до своего отказа и после отказа не ремонтировались.
Необходимо по данным экспериментам построить график изменения вероятности безотказной работы.
Для оценки
вероятности безотказной работы
системы
по экспериментальным данным используем
метод Каплана-Майера
;
Где
-
число изделий, оставшихся в работоспособном
состоянии на момент времени
Остальные значения рассчитываем аналогично и заносим в таблицу 1
Таблица.1
|
|
|
|
1 |
2 |
0,975 |
0,975 |
2 |
4,24 |
0,974 |
0,950 |
3 |
6,76 |
0,974 |
0,925 |
4 |
7,22 |
0,973 |
0,900 |
5 |
8,4 |
0,972 |
0,875 |
6 |
12,8 |
0,971 |
0,850 |
7 |
28 |
0,971 |
0,825 |
8 |
34,9 |
0,970 |
0,800 |
9 |
38,3 |
0,969 |
0,775 |
10 |
38,8 |
0,968 |
0,750 |
11 |
47 |
0,967 |
0,725 |
12 |
47,7 |
0,966 |
0,700 |
13 |
48,4 |
0,964 |
0,675 |
14 |
51,6 |
0,963 |
0,650 |
15 |
59,1 |
0,962 |
0,625 |
16 |
63,5 |
0,960 |
0,600 |
17 |
65,7 |
0,958 |
0,575 |
18 |
68,6 |
0,957 |
0,550 |
19 |
71,9 |
0,955 |
0,525 |
20 |
73,7 |
0,952 |
0,500 |
21 |
74,7 |
0,950 |
0,475 |
22 |
78,2 |
0,947 |
0,450 |
23 |
78,8 |
0,944 |
0,425 |
24 |
81,7 |
0,941 |
0,400 |
25 |
88,9 |
0,938 |
0,375 |
26 |
96,1 |
0,933 |
0,350 |
27 |
102 |
0,929 |
0,325 |
28 |
103 |
0,923 |
0,300 |
29 |
109 |
0,917 |
0,275 |
30 |
113 |
0,909 |
0,250 |
31 |
117 |
0,900 |
0,225 |
32 |
122 |
0,889 |
0,200 |
33 |
127 |
0,875 |
0,175 |
34 |
129 |
0,857 |
0,150 |
35 |
142 |
0,833 |
0,125 |
36 |
143 |
0,800 |
0,100 |
37 |
235 |
0,750 |
0,075 |
38 |
291 |
0,667 |
0,050 |
39 |
327 |
0,500 |
0,025 |
40 |
420 |
0,000 |
0,000 |
,28По данным таблицы строим график изменения вероятности безотказной работы системы (рис.1)
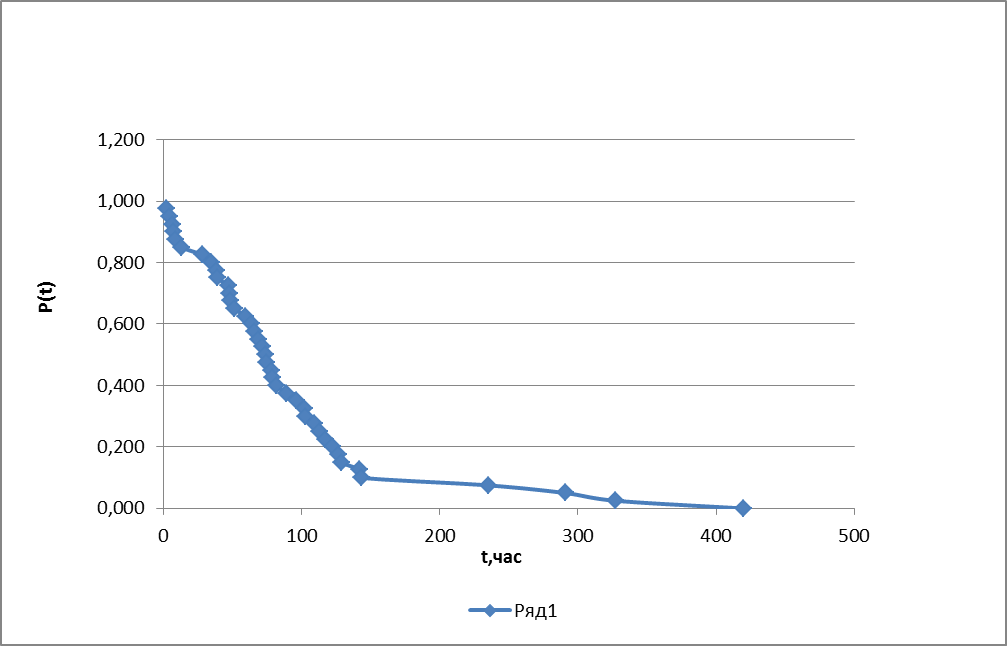
Рис. 1. Вероятность безотказной работы системы
Ответ: На основание Рис.1 принимаем мультимодальное распределение