4.3. Пример выполнения расчетно-графической работы

Найти скорости и ускорения ползуна В, точек А и М шатуна АВ нецентрального кривошипно-ползунного механизма, когда кривошип ОА образует с горизонтальной осью угол 30^{o (рис.4.6). В рассматриваемый момент времени вращение кривошипа происходит с угловой скоростью ω}_ОА^{=1,5 рад/c и угловым ускорением ε}_ОА^{=2 рад/с2, а ОА=0,4 м, АВ=0,8 м, АМ=0,2 м, ОС=0,2м.}

30^o

Решение. Расчет скоростей.

Точка А механизма принадлежит кривошипу ОА и шатуну АВ. Кривошип ОА вращается вокруг оси О с угловой скоростью ω_ОА, поэтому скорость точки А равна:

м/с.

В ектор V_A скорости точки А направлен перпендикулярно кривошипу ОА в сторону его вращения.

Т очка В механизма является общей для шатуна АВ и ползуна В. Поскольку ползун В движется в горизонтальных направляющих, то его, скорость V_B направлена вдоль оси Вх. Строим перпендикуляры к скоростям в точках А и В шатуна: их точка пересечения совпадает с мгновенным центром скоростей С_V шатуна АВ. Векторы скоростей точек изображены на рис. 4.7.

Для продолжения расчета скоростей необходимо вычислить длины прямолинейных отрезков АС_V, BC_V и MC_V.

Из прямоугольного треугольника ОАЕ имеем:

м.

Из рис. 4.6 видно что:

м.

Треугольник АВD – прямоугольный, поэтому:

,

то есть угол α=30^o.

М

О

ω_ОА

С

D

ω_AB

C_V

V_A

A

V_М

30^o

E

В

α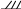

x

V_B

Рис. 4.7

Из построений, приведенных на рис. 4.7, видно также, что:

АВС_V = BAС_V =60^{o, поэтому треугольник} АВС_V – равносторонний, следовательно,

м.

Мгновенную угловую скорость ω_АВ вращения шатуна АВ вычисляем по формуле:

рад/с.

Модуль скорости ползуна В равен

м/с.

В ектор V_В скорости ползуна В направлен в отрицательную сторону оси Вх.

Из треугольника АМС_V по теореме косинусов имеем:

Скорость V_M точки М находим по формуле:

м/с.

В ектор V_M скорости точки М направлен перпендикулярно отрезку прямой МС_V (рис. 4.7).

Расчет ускорений.

Ускорение точки А кривошипа ОА равно векторной сумме касательного и нормального ускорений:

Модули касательного и нормального ускорений точки А вычисляем по формулам:

м/с²;

м/с².

Вектор касательного ускорения точки А перпендикулярен кривошипу ОА и его направление совпадает с вектором V_А скорости точки А, так как кривошип вращается ускоренно. Что же касается вектора нормального ускорения точки А, то он направлен вдоль кривошипа ОА к его оси вращения О (рис. 4.8). Очевидно, что модуль ускорения точки А определится по теореме Пифагора:

Шатун АВ совершает плоское движение. Возьмем за полюс точку А шатуна и запишем векторное равенство, определяющее ускорение точки В шатуна:

(4.1)

Модули касательного a_ВА^τ и нормального a_ВАⁿ ускорений точки В вокруг полюса А определяем по формулам:

.

м/с².

В екторы a_ВА^τ и a_ВАⁿ изображены на рис. 4.8. Ориентация вектора a_ВА^τ соответствует принятому ускоренному вращению (ε_АВ) шатуна АВ.

Д ля определения мгновенного углового ускорения ε_АВ шатуна АВ используется то обстоятельство, что вектор a_B ускорения ползуна В направлен вдоль оси Вх, поэтому a_By=0. Проецируя обе части векторного равенства (4.1) на ось By, будем иметь:

откуда:

м/c².

Тогда:

рад/с².

Полученное положительное значение мгновенного углового ускорения ε_АВ свидетельствует о том, что принятое для него на рис. 4.8 направление соответствует действительному.

Проекция a_Вх ускорения ползуна В на ось Вх равна:

м/с².

Поскольку проекция a_Вy=0, то м/с².

Очевидно, что вектор a_В ускорения ползуна В ориентирован в отрицательном направлении оси Вx.

Для определения ускорения точки М (точка А -- полюс) имеем

(4.2)

Модули касательного a_МА^τ и нормального a_МАⁿ ускорений точки М вокруг полюса А равны:

м/с².

м/с².

В екторы a_МА^τ и a_МАⁿ изображены на рис. 4.8.

Проецируя обе части векторного равенства (4.2) на координатные оси, получаем:

Таким образом, модуль ускорения точки М равен: