Санкт-Петербургский Политехнический Университет

Институту Машиностроения

Курсовая работа по Инженерный анализ в САПР

на тему:

«Математические модели в процедурах анализа на макроуровне,

Математическое обеспечение анализа на системном уровне, Методика проектирования автоматизированных систем»

Выполнил студент группы 5001

Ленков А.В.

Принял

Никитин А.В.

Санкт-Петербург

2014 год

Оглавление

1. Ведение, 3

2. Математические модели в процедурах анализа на макроуровне, 4

3. Математическое обеспечение анализа на системном уровне, 9

4. Методика проектирования автоматизированных систем, 21

5. Литература 40

1. Введение

Российская промышленность растет. Это подтверждают и сухие факты статистики, и участники рынка. Макроэкономические причины, обеспечивающие рост, известны, хотя и не перестают быть предметом обсуждений и споров. Гораздо менее понятны внутренние источники этого роста. Попробуем проанализировать «историческую подоплеку» ситуации. Все крупные предприятия пережили последнюю реконструкцию не позднее середины восьмидесятых годов прошлого века (редкие исключения более поздней модернизации лишь подтверждают это правило). В тот исторический период зачастую строились предприятия максимальной производительности (в рамках плановой экономики казалось оправданным строительство гигантов с самой высокой в мире производительностью) и замкнутого цикла (т. е. с очень высокой глубиной производства — «до последнего болта» все делать самим). Таким образом, большинство крупных предприятий оказались построенными по принципам серийного и крупносерийного (а иногда и массового) производства.

2. Математические модели в процедурах анализа на макроуровне

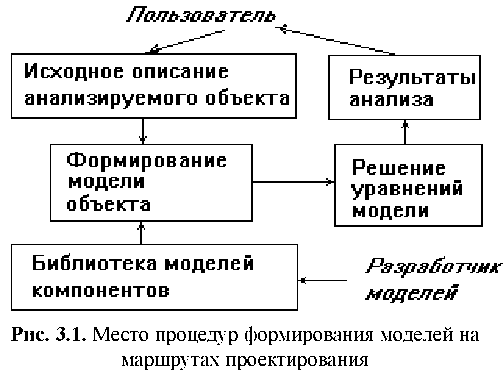
Исходные уравнения моделей. Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели. В этом параграфе изложен обобщенный подход к формированию алгоритмических моделей на макроуровне, справедливый для большинства приложений.

Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.

Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов (ММЭ).

Топологические уравнения описывают взаимосвязи в составе моделируемой системы.

В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).

Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях

компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.

Различают фазовые переменные двух типов, их обобщенные наименования — фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение — связи между однотипными фазовыми переменными в разных компонентах.

Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.

Примеры компонентных и топологических уравнений. Рассмотрим несколько типов систем.

Э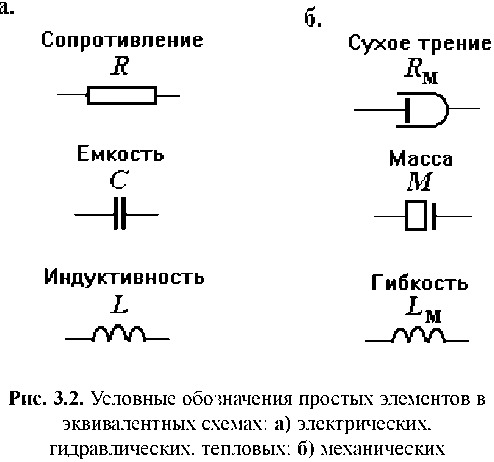 лектрические системы. В электрических системах фазовыми переменными являются электрические напряжения и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные двух- и многополюсные компоненты. К простым двухполюсникам относятся следующие элементы: сопротивление, емкость и индуктивность, характеризуемые одноименными параметрами R, C, L. В эквивалентных схемах эти элементы обозначают в соответствии с рис. 3.2,а.

Диссипативные свойства в механических системах твердых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причем в этих соотношениях производные сил или скоростей не фигурируют, как и в случае описания с помощью закона Ома диссипативных свойств в электрических системах.

Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера), во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.