Статическая детерминированная модель управления запасами без дефицита

Предположение о том, что дефицит не допускается, означает полное удовлетворение спроса на запасаемый продукт, т.е. совпа­дение функций r(t) и b(t). Пусть общее потребление запасаемого продукта за рассматриваемый интервал времени 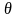равно N. Рас­смотрим простейшую модель, в которой предполагается, что рас­ходование запаса происходит непрерывно с постоянной интен­сивностью, т.е. 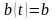. Эту интенсивность можно найти, разде­лив общее потребление продукта на время, в течение которого он расходуется:

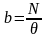(1)

Пополнение заказа происходит партиями одинакового объема, т.е. функция а(t) не является непрерывной: a(t) = 0 при всех t, кроме моментов поставки продукта, когда a(t)= n, где п - объем партии. Так как интенсивность расхода равна b, то вся партия будет использована за время

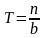(2)

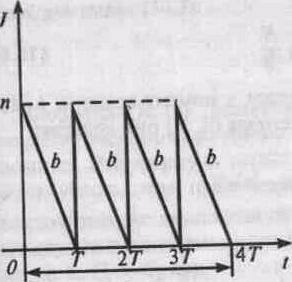
Рис. 1

Рис. 2

Если отсчет времени начать с момента поступления первой партии, то уровень запаса в начальный момент равен объему этой партии п, т.е. J(0) = n. Графически уровень запаса в зависимости от времени представлен на рис 1.

На временном интервале [0,T] уровень запаса уменьшается по прямой J(t)= п-bt от значения п до нуля. Так как дефицит не допускается, то в момент Т уровень запаса мгновенно пополняет­ся до прежнего значения п за счет поступления партии заказа. И так процесс изменения J(t) повторяется на каждом временном интервале продолжительностью Т (см. рис.1).

Задача управления запасами состоит в определении такого объе­ма партии п, при котором суммарные затраты на создание и хране­ние запаса были бы минимальными.

Обозначим суммарные затраты через С, затраты на создание запаса — через C₁, затраты на хранение запаса — через C₂ и най­дем эти величины за весь промежуток времени Т.

Пусть затраты на доставку одной партии продукта, не зависи­мые от объема партии, равны c₁, а затраты на хранение одной единицы продукта в единицу времени — с₂;. Так как за время необходимо запастись N единицами продукта, который доставля­ется партиями объема п, то число таких партий k равно:

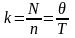(3)

Отсюда получаем (4)

Мгновенные затраты хранения запаса в момент времени t рав­ны 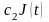. Значит, за промежуток времени [0, Т] они составят

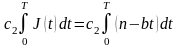
или, учитывая (2):

.

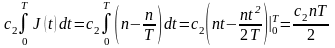Средний запас за промежуток [0, Т] равен пT/2, т.е. затраты на хранение всего запаса при линейном (по времени) его расходе рав­ны затратам на хранение среднего запаса.

Учитывая периодичность функции J(t) (всего за промежуток времени будет k =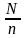 "зубцов", аналогичных рассмотренному на отрезке [0,T] ), и формулу (3), получаем, что затраты хранения запаса за промежуток времени равны:

(5)

Нетрудно заметить, что затраты С₁ обратно пропорциональны, а затраты С₂ прямо пропорциональны объему партии п. Графики функци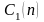й и 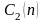, а также функции суммарных затрат

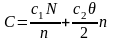(6)

приведены на рис.2. В точке минимума функции С(n) ее производная

,

откуда 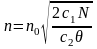(7)

или, учитывая (1)

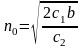(8)

Формула (8), называемая формулой Уилсона или формулой наиболее экономичного объема партии, широко используется в эко­номике. Эта формула может быть получена и другим способом, если учесть, что произведение есть величина постоянная, не зависящая от п. В этом случае, как известно, сум­ма двух величин принимает наименьшее значение, когда они рав­ны, т. е. 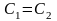или

(9)

откуда получаем (7).

Из (9) следует, что минимум общих затрат задачи управле­ния запасами достигается тогда, когда затраты на создание запаса равны затратам на хранение запаса. При этом минимальные сум­марные затраты

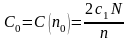, (10)

откуда, с учетом предыдущего, получим

или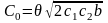 . (11)

Число оптимальных партий за время с учетом (2), (7) и (1) равно:

.

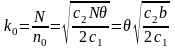Время расхода оптимальной партии равно

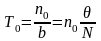
или

Пример.

Потребность сборочного предприятия в деталях некоторого типа составляет 120 000 деталей в год, причем эти детали расхо­дуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объ­ема, указанного в заказе. Хранение детали на складе стоит 0,35 ден. ед. в сутки, а поставка партии -10 000 ден. ед. Задержка произ­водства из-за отсутствия деталей недопустима. Определить наибо­лее экономичный объем партии и интервал между поставками, которые нужно указать в заказе (предполагается, что поставщик не допускает задержки поставок).

Решение.

По условию затраты на одну партию составляют C = 10 000 ден. ед., затраты хранения единицы запаса в сутки = 0,35 ден. ед. Общий промежуток времени = 1 год = 365 дней, а общий объем запаса за этот период N = 120 000 деталей. По формуле (7)

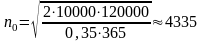, дет., а по (2)

дней.

Итак, наиболее экономичный объем партии равен 4335 дета­лей, а интервал между поставками 13 дней.

На практике, естественно, объем партии может отличаться от оптимального п₀, вычисленного по (7). Так, в предыдущей за­даче может оказаться удобным заказывать партии по 4 500 или даже по 5 000 деталей и возникает вопрос, как при этом изменят­ся суммарные затраты.