14. Арифметические операции над непрерывными функциями. Суперпозиция функций. Теорема о непрерывности сложной функции.

Теор.5.2.1 о непрерывности суммы, произведения, частного. Пусть функции f(x), g(x) непрерывны в точке х0. Тогда в этой точке непрерывны функции f(x)g(x), f(x)g(x),   (частное - в случае, когда g(х0)0).

Док-во непосредственно следует из теор.4.4.10 раздела 4.4.6 "Арифметические действия с пределами". Для примера докажем непрерывность частного. Пусть f(x), g(x) непрерывны в точке х0, т.е.  ,  , причём g(х0)0. По теор.4.4.10 существует  , и этот предел равен  , что означает непрерывность функции   в точке х0. Курс лекций по математике Уравнение плоскости Решение дифференциальных уравнений

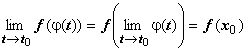Теор.5.2.2 о переходе к пределу под знаком непрерывной функции. Пусть функция    определена в некоторой окрестности точки t0 и имеет  , равный х0. Пусть точка   принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда существует , и  . Дифференциал (от лат. differentia — разность, различие) в математике, главная линейная часть приращения функции

Док-во. Возьмём 0. Так как f(x) непрерывна в точке х0, то 0, такое что  х- х0   f(x)- f(x0). Так как существует  = х0, то для  0, такое что 0< t- t0 

  (t)- х0. Таким образом, для 0 мы нашли такое 0, что из 0< t- t0

  f(x)- f(x0)=  f( (t))- f( ), что означает существование предела  и равенство этого предела величине  .

Теор.5.2.3 о непрерывности суперпозиции непрерывных функций. Пусть функция    непрерывна в точке точке t0. Пусть точка   принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда сложная функция   непрерывна в точке t0.

Док-во непосредственно следует из предыдущей теоремы. Так как  (t) непрерывна в точке t0, то  . Поэтому 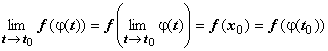 , что и означает непрерывность сложной функции  в точке t0.

Введём понятие сложной функции. Пусть функции   и   определены на множестве X и Y соответственно, причём множество значений функции   содержится в области определения функции f Тогда функцию, принимающую при каждом  значение  , называют сложной функцией или суперпозицией (композицией) функций   и f и обозначают  .

Теорема. Если функция z=f(y) непрерывна в точке  , а функция   непрерывна в точке   , причём   , то в некоторой окрестности точки   определена сложная функция  , и эта функция непрерывна в точке   .

○ Пусть задано произвольное число  . В силу непрерывности функции f в точке  существует число   такое, что   и

 (2)

где  .

В силу непрерывности функции   в точке   для найденного в (2) числа 

можно указать число   такое, что

 (2')

Из условий (2) и (2') следует, что на множестве   определена сложная функция , причём

 ,

где  , т.е.

.

Это означает, в силу определения непрерывности, что функция   непрерывна в точке  .●

15. Точки разрыва функции. Их классификация. Примеры. Определение точки разрыва

Определение

Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция 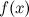  определена в точке и ее окрестности;

2. существует конечный предел функции   в точке  ;

3. это предел равен значению функции в точке  , т.е. 

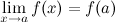
называется точкой разрыва функции.

Пример

Функция   не определена в точке  , а значит, эта точка является точкой разрыва указанной функции.