16 Задачи и методы силового расчёта механизмов.

Задачи:

-определение сил, действующих на звенья или на связи механизма;

-определение уравновешивающей силы (уравновешивающего момента) на входном звене.

Цели:

-накопление необходимых данных для последующего проектирования и конструирования механизма.

Методы решения:

-принцип Даламбера: если добавить силу энерции, то система будет находиться в мгновенном равновесии и к ней применимы все законы статики;

-состояние механической системы не изменится, если связи отбросить, а их действие заменить реакциями:

Основным методом силового расчета механизмов является кинетостатический метод. Этот метод, на основании принципа Даламбера, приводит задачи динамики машин к задачам статики. При определении условий равновесия отдельных звеньев машин, кроме действующих на них внешних сил, принимаются в расчет также внутренние силы инерции. Силовой расчет дает возможность правильно, по условиям прочности, выбрать конструктивную форму и размеры отдельных звеньев и деталей машин, определить давления и силы трения в кинематических парах, а также правильно оценить необходимую мощность для привода машины или механизма.

17 Определение сил инерции.

Сила инерции – фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем. В математических вычислениях введения этой силы происходит путём преобразования уравнения F1+F2+…Fn = ma к виду

F1+F2+…Fn–ma = 0, где Fn – реально действующая сила, а ma – «сила инерции».

Закон инерции про инерционные системы отсчёта гласит, что без влияния неуравновешенных сил тело будет сохранять свою скорость или неподвижность. В качестве примера силы инерции можно рассмотреть простую силу инерции, которую можно ввести в равноускоренной системе отсчёта:

Написать пример с быстро останавливающимся автобусом полным пассажирами.

Среди сил инерции выделяют следующие:

• простую силу инерции, которую мы только что рассмотрели;

• центробежную силу, объясняющую стремление тел улететь от центра во вращающихся системах отсчёта;

• силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся системах отсчёта;

С точки зрения общей теории относительности, гравитационные силы в любой точке – это силы инерции в данной точке искривлённого пространства Эйнштейна (см. принцип эквивалентности).

18 Условие статической определимости кинематических цепей.

Необходимо помнить, что кинематические цепи, имеющие степень подвижности w=0, в силовом отношении являются статически определенными. Условие статической определимости плоских кинематических цепей записывается в виде: 3n - 2p₅ - p₄ = 0 где n - число подвижных звеньев P₅ и P₄ число кинемат пар 5 и 4 класса, 3 – число уравнений статики, которое можно составить для каждого подвижного звена в плоскости.

Плоская кинематическая цепь может состоять из кинематических пар 5-го класса (вращательных, поступательных) и пар 4-го класса (высших, у которых звенья соприкасаются в точке. Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности.

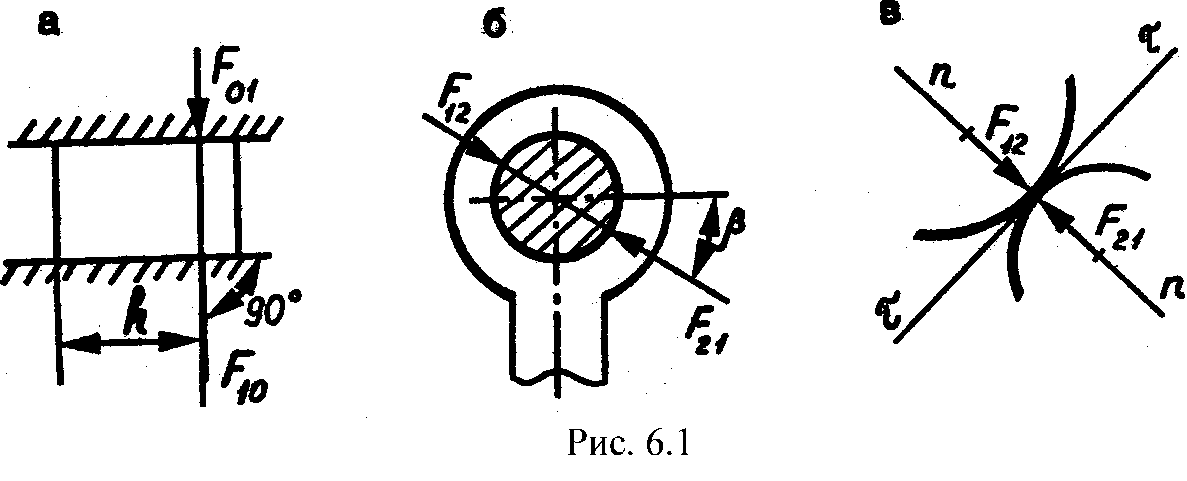
В поступательной паре (рис .6.1, а) реакции направлены перпендикулярно направляющей. Неизвестных здесь две: величина силы F01 и точка ее приложения (расстояние h). Во вращательной паре равнодействующая сил реакции направлена по нормали к цилиндрической поверхности, т.е. проходит через центр шарнира (рис. 6.1, б). Неизвестными являются : направление реакции (угол β) и величина силы. Таким образом, эта пара также вносит в уравнения кинетостатики две неизвестных. Следовательно, от каждой силы, действующей в любой низшей кинематической паре, в расчетных уравнениях появляются две неизвестные величины.

В высших парах сила взаимодействия между звеньями направлена по общей нормали и приложена в точке касания, т.е. известны и направление и точка приложения силы (рис. 6.1, в), неизвестна лишь ее величина. Поэтому в расчетных уравнениях члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.

В общем виде общ числ неизвестн Nн = 2⋅p5+ p4(6.2)

Число уравнений статики для каждого звена плоского механизма равно 3, значит, общее число уравнений для n подвижных звеньев Nу =3n. (6.3)

Чтобы система была статически определимой, число уравнений Nу должно быть равно числу неизвестных Nн . Приравниваем (6.2) и (6.3), после чего получим: 3n = 2⋅p5+ p4. (56.4)

Если заменить высшие пары низшими, то получим 3n = 2⋅p5. (5.4)

Из этого можно сделать вывод, что группы Ассура являются статически определимыми.

На основании вышеизложенного формулируется общая методика силового анализа: расчет необходимо проводить по структурным группам, начиная с наиболее удаленной от начального звена и заканчивая начальным звеном (механизмом I класса). Таким образом, силовой расчет проводится в порядке, обратном кинематическому.