32 Основные геометрические параметры зубчатого колеса.

Основными параметрами зубчатого колеса являются (рис. 1):

• z – число зубьев;

• r_a – радиус (диаметр) окружности выступов;

• r_f – радиус (диаметр) окружности впадин;

• r_b – радиус (диаметр) основной окружности;

• r – радиус (диаметр) делительной окружности, т. е. окружности, которая  является  начальной  в станочном зацеплении колеса с режущим инструментом;

• р – шаг по делительной окружности;

• h – высота зуба, равная h=h_a+h_f, где:

h_a – высота головки зуба;

h_f – высота ножки зуба;

• m – модуль зацепления, определяемый из условия:

2πr = zp, т.е. 2r/z = pπ = m (измеряется в мм).

Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля. Обычно размеры зубчатого колеса и зубьев выражаются через m.

Т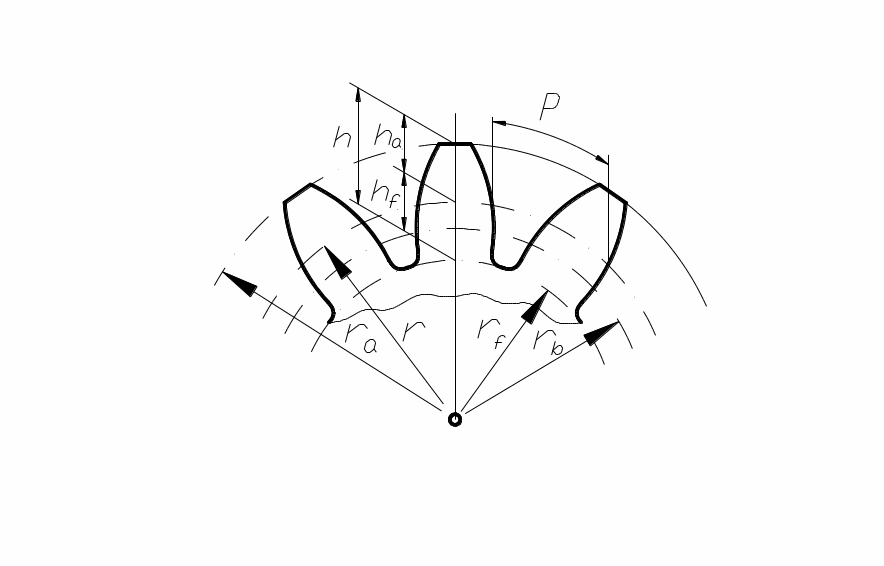 ак, например:h_a = h_a’·m, где h_a’  – коэффициент  высоты головки зуба;

h_f = ( h_a’+ c^/)·m, где c^/- коэффициент  радиального зазора;

r=0.5·m·z; p=π·m; r_b= r·cosα = 0.5·m·z·cosα, где α-угол исходного контура режущего инструмента. Обычно для стандартных зубчатых колёс: h_a’=1; c^/ =0,25; α=20º.

33 Свойства эвольвентного зацепления

В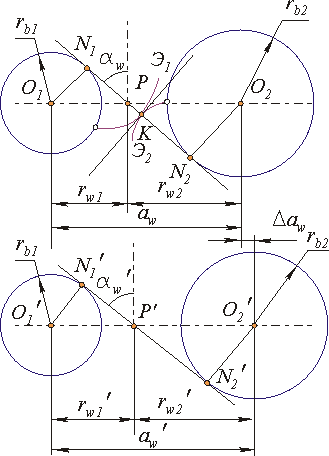 зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства.

Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной.(1)

Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется.(2)

Свойство 3. При изменении межосевого расстояния в эаольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.(3)

Свойство 4. За пределами отрезка линии зацепления N1N2 рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.

(1)

( 2)

(3)

34 Качественные показатели зубчатого зацепления

Одним из качественных показателей зубчатой передачи является коэффициент перекрытия ε_α, равный ε_α=g_α/p_α, где p_α – шаг по основной окружности (расстояние между одноименными точками двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент ε_α показывает сколько пар зубьев в среднем одновременно находиться в зацеплении. Для прямозубой передачи обычно 1< ε_α<2. Чем больше ε_α, тем более плавно и бесшумно работает передача.

Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и ее кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:

V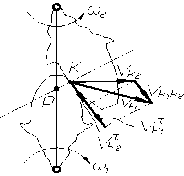 _k1 – скорость точки К первого колеса;

V_k1^t – проекция этой скорости на касательную к контактирующим профилям;

V_k2 и V_k2^t – тоже для колеса 2.

Скорость скольжения колеса 1 и 2 относительно друг друга равна:

V_ck=V_k1k2= V_k1^t- V_k2^t

Коэффициенты скольжения колес 1 и 2 равны: λ₁= V_ck / V_k1^t ; λ= V_ck / V_k2^t

Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления.