30 Основная теорема зубчатого зацепления. Теорема Виллиса
Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость (-ω2), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а).
Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к. i1,2=ω1/ω2 = rw1/rw2=const
Точка контакта зубьев (точка К), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость Vk ┴ PK и совпадает с общей касательной к профилям в точке К при условии постоянства этого контакта.
В противном случае постоянного контакта не будет, так как появится Vk” и профили разомкнутся. Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.
Нормаль NN к касающимся профилям зубьев, проведенная через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.
Эта теорема, сформулированная Виллисом в 1841г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.
31 Эвольвента окружности её уравнение и своиства.
Эвольвентой
называется кривая, очерчиваемая точкой
прямой, при перекатывании этой прямой
по окружности без проскальзывания (рис.
1). В теории зацепления прямую называют
производящей (образующей), а окружность
– основной окружностью (радиус rb).
Рассмотрим построение эвольвенты Е
(рис. 1).В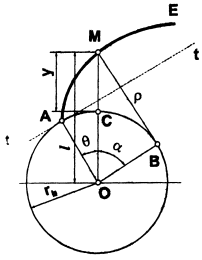
произвольной точке эвольвенты М
проведем нормаль, которая касается
основной окружности в точке В,
получаем радиус кривизны эвольвенты
ρ.
Из прямоугольного треугольника ΔОВМ найдем катет МВ: MB= rb·tgα.
Из условия образования эвольвенты радиус кривизны МВ должен быть равен длине развертываемой дуги АВ основной окружности:АВ = rb (+),
rb· tgα = rb (+), где полярный угол наклона радиус вектора; угол между направлением радиус вектора и направлением радиуса основной окружности проведенного в точке касания нормали. Отсюда: = tgα – α = invα
Разность тангенса и угла представляет собой эвольвентную функцию называемую инволютой. Инволюта является параметром для геометрических расчетов зубчатых механизмов.
Свойства эвольвенты:
-эвольвента не имеет точек внутри основной окружности, начин с осн окружн;
-нормаль к точке эвольвенты направлена по касательной к основной окружности;
-центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью.