
- •163 Теорема о необходимом условии экстремуме фоп.
- •162 Определение локального экстремума
- •142 Определение дифференцируемой в точке функции
- •141 Определение нормаль
- •140 Определение касательной
- •139 Геометрический смысл производной
- •138 Определение производной функции одной переменной
- •131 Теорема Коши (о промежуточных значениях функции)
- •130 Теорема Больцано-Коши (о нуле функции)
- •129 Определение точек разрыва второго рода
- •128 Определение точек разрыва первого рода
- •127 Определение точки разрыва функции
1) Числовая матрица-набор чисел (mxn),записанных в виде прямоугольной таблицы.
2)Строка – матрица А (nx1).Столбец – матрица А (1хn).
3)Квадратная матрица- матрица А (nxn),т.е.количество строк равно количеству столбцов.
4)Главная диагональ матрицы – набор элементов (a11,a22,a33…ann).
5)Нулевая матрица- матрица, все элементы которой нули.
6)Единичная матрица – квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы нули.
7)Равные матрицы , если A(aij)=B(bij).
8)Сумма матриц А и В – такая матрица А+В=С, что каждый ее элемент вычислен по формуле:
Сij=aij+bij (складывать можно матрицы одной размерности).
9)Произведением матрицы А на число α- матрица αА=В:bij= α*aij.
10)Произведением матрицы А(aik)и B(bkj); где i=1,m; k=1,l; j=1,n; наз. С=А+В:
Cij=ai1*b1j+ai2*b2j+…+ail+blj=∑;
![]() .
Произведение матриц возможно только,
когда кол. столбцов 1м-цы=кол. строк
2м-цы.
.
Произведение матриц возможно только,
когда кол. столбцов 1м-цы=кол. строк
2м-цы.
11)Транспонированная матрица - если строки АT явл. столбцами А.
12)Транспонированием матрицы наз.операцию замены строк матрицы ее столбцами,а столбцов строками.
13)Симметрической матрицей называют квадратную матрицу, элементы которой симметричны относительно главной диагонали: АT=A, т.е.aij=aji.
14)Квадратная м-ца
наз. кососимметрической, если:![]()
![]() :
:
15)Определитель матрицы - число характеризующее квадратную м-цу.
16)Определителем м-цы 1го порядка (одноэлементной) наз. сам элемент.
Определителем м-цы 2го порядка наз. число, вычисляемое по ф-ле:│А│=a11*a22-a12*a21.
Определителем м-цы
3го порядка наз. число, выч-е по ф-ле:
![]()
Правило Сарруса
(п-ло треуг-в):
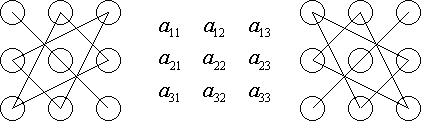
Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
17)Минор эл-та м-цы – опр-ль м-цы, кот. получ. из м-цы A(nxn) вычеркиванием i-той строки и j-того столбца.
18)Алгебраическим
дополнением Аij элемента
аij матрицы
n-го
порядка называется его минор, взятый
со знаком, зависящий от номера строки
и номера столбца:
![]() .
.
19)Теорема
Лапласа (об определителе матрицы).
Определитель квадратной матрицы равен
сумме произведений элементов любой
строки (столбца) на их алгебраические
дополнения:
![]() (*)
(разложение по элементам i-й
строки);
(*)
(разложение по элементам i-й
строки);
![]() (**)(разложение
по элементам j-го
столбца).
(**)(разложение
по элементам j-го
столбца).
20)Св-ва определителя:1)если какая-либо сторона м-цы сост.из одних нулей,то ее опред.равен 0;2)если все эл-ты какой-либо строки м-цы умнож.на число,то ее опред-ль умнож.на это число;3)при транспон-и м-цы опр-ль не измен-ся │АТ│=│А│;4)при перестановке 2х строк опр-ль м-цы меняет знак на противопол-й;5)если квадр.м-ца содерж.2 одинак.строки,то ее опред-ль=0;6)если эл-ты 2х строк м-цы пропорц-ны,то ее опр-ль=0;7)сумма пр-ий эл-в какой-либо строки м-цына алг.допол.эл-тов др.строки этой м-цы =0;8)опр-ль м-цы не измен-ся, если к эл-там какой-либо строки прибавить эл-ты др.строки умнож-ные на одно и тоже число;9)опр-ль произв-я 2х квадр.м-ц=произ-ю их опр-лей(м-цы одинак.порядка);10)опр-ль диаг-ной м-цы=произ-ю диаг.эл-в.(для гл.диаг-ли).
21)
Ступенчатая матрица
— матрица,
имеющая m строк,
у которой первые r
диагональных элементов ненулевые,
r ≤ m,
а элементы, лежащие ниже диагонали и
элементы последних m − r строк
равны нулю:
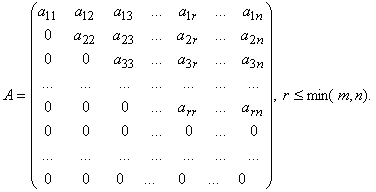
22)Минором к-того порядка м-цы А(Мк) наз.опр-ль к-того порядка составленный из к-строк и к-столбцов данной м-цы произвольным образом.
23)Ранг м-цы-наивысший порядок отличного от нуля минора этой м-цы:rang(A);r(A).Из определения =>1)r(A)больше либо равно min(m,n),где m-кол.строк,n-кол.столбцов;2)r(A)=n│A│≠0 и Аnxn.
24) Определение линейной комбинации строк (столбцов) матрицы.
Столбец ![]() называется линейной
комбинацией столбцов
называется линейной
комбинацией столбцов ![]() одинаковых
размеров, если
одинаковых
размеров, если![]() (сумме
произведений этих строк на какие-либо
числа), где
(сумме
произведений этих строк на какие-либо
числа), где ![]() —
некоторые числа.
—
некоторые числа.
25)
Определение линейно зависимых строк
(столбцов) матрицы. Система
из ![]() столбцов
называется
линейно зависимой, если существуют
такие числа
,
не все равные нулю одновременно, что
столбцов
называется
линейно зависимой, если существуют
такие числа
,
не все равные нулю одновременно, что![]()
26) Теорема о ранге матрицы. Ранг м-цы= макс.числу ее линейно независ.(базисных)строк, через кот. линейно выраж. ост. строки(аналог.со столбцами).
27)Базисные строки - линейно не зависимые строки м-цы.
28)Обратная
м-ца - А-1
наз.обрат.м-цей по отнош-ю к квадр.м-це
А,если
![]() ,
где
,
где ![]() -
это единичная матрица соответствующего
порядка.
-
это единичная матрица соответствующего
порядка.
29)Вырожденная м-ца- если │А│=0.
30)Определение
системы линейных уравнений (СЛУ).
Системой m линейных
уравнений с n неизвестными ![]() называется
система S вида
называется
система S вида
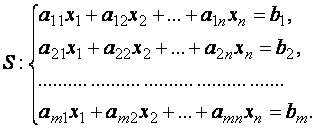 ,где
,где ![]() коэффициенты
при неизвестных,
коэффициенты
при неизвестных, ![]() свободные
члены (
свободные
члены (![]() ,
, ![]() заданные
числа).
заданные
числа).
31)Решением
системы вида ![]() aijxj=bi,
i=1,m
наз.такую совокупность чисел
x1=к;х2=к,...,хn=kn,кот.при
подстановке в каждое ур-не сист.обращает
ур-не в тождество.
aijxj=bi,
i=1,m
наз.такую совокупность чисел
x1=к;х2=к,...,хn=kn,кот.при
подстановке в каждое ур-не сист.обращает
ур-не в тождество.
32)Совместная СЛУ – если она имеет хотя – бы одно решение.
33) Несовместная СЛУ – если она не имеет решений.
34)Определенная СЛУ – совместная СЛУ, кот.имеет единствен-е реш-е.
35)Неопределенная СЛУ – совмест.СЛУ, кот.имеет более одного реш-я.
36)Равносильными наз.две сист. кот. имеют одинак.реш-я.
37) Теорема Кронекера – Капели.Система СЛУ совместна тогда и только тогда, когда ранг м-цы сист.равен рангу расшир.этой сист.,т.е. r(A)=r(A│b).
Если ранг м-цы совмест.сист.=чису переменных,то сист.имеет единст.реш-е. Если ранг м-цы совмест.сист.меньше числа переменной, то сист.неопред.и имеет бесконеч.множ-во реш-ий.
38) Определение системы линейных однородных уравнений. СЛОУ: АХ=О, где О- нулевой столбец.
39)Вектором АВ наз. направл. отрезок [A;B] с начал.точкой(т.)А и конеч.т. В(a).
40)Длиной вектора │АВ│(модулем)наз.число=длине отрезка АВ.
41)Коллинеарные векторы – векторы, лежащие на одной прямой или на ││прямых.
42)Нулевой вектор – вектор, у кот. совпадают начало и конец.
43)Суммой 2х векторов А+b наз. вектор с=a+b начало кот. совпад. с началом a и конец совпад.с концом b.
44)Произведением вектора на число наз.вектор αa=b, такой, что │b│=α│a│, при α≥0. -α│a│;при α<0, направление кот. совпад. при α.0; при α>0, и противополож.напр.α<0.
45)Единичный вектор-вектор длина,кот.равна 1. е: │е│=1.
46)Координатами вектора наз. корд. его конца, если начало совпад. с началом корд.
47)Направляющие векторы осей i,j,k соотвественно ОX,OY,OZ. Эти векторы наз.единичными и напр.вдоль соотв. осей.
48) Ортонормированный базис пространства - векторы i,j,k.
49) Определение разложение вектора по базису (по заданным векторам). Линейной комбинацией векторов a1, ..., an с коэффициентами x1, ..., xn называется вектор x1a1 + ... + xnan.Чтобы разложить, вектор b по базисным векторам a1, ..., an, необходимо найти коэффициенты x1, ..., xn, при которых линейная комбинация векторов a1, ...,an равна вектору b,x1a1+ ... + xnan= b, при этом коэффициенты x1, ..., xn, называются координатами вектора b в базисеa1, ..., an.
50)Радиусом-вектором т. М наз. вектор r=OM=xi+yj+zk, где М(x,y,z).
51)Проекцией вектора АВ на ось l наз.величину(длину) напр.отрезка CD из т. А в В опуск. перпендикуляр и Pr l(AB)= │CD│.
52)Скалярное произ-е векторов (a,b) – число равное │a││b│cos f(f=a,b).
53)Направляющими косинусами вектора а наз.косинусы углов, кот. этот вектор сост. с осями корд.
54)Векторным произ-ем векторов а на b [a;b] или (axb), наз. вектор, удовлетвор.след.св-вам:1) │[a,b] │=│a││b│sin f; 2) [a;b]┴a;[a;b]┴b;
3)[a,b] напрвл.так, что из конца кратчайший поворот от a к b виден проходящ. против часовой стрелки.
55)Смешанным произ-м векторов a,b,c, наз. скалярное пр-е ([a,b];c)
56) Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
I. ![]() II.
II. ![]() III.
III. ![]() (нулевой
элемент, такой, что
(нулевой
элемент, такой, что ![]() ). IV.
). IV. ![]() (элемент,
противоположный элементу
(элемент,
противоположный элементу ![]() ),
такой, что
),
такой, что ![]() V.
V. ![]() VI.
VI. ![]() VII.
VII. ![]() VIII.
VIII. ![]() Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
57)
Размерность
линейного пространства Линейное
пространство V называется n-мерным
(имеет размерность n),
если в нем: 1) существует n линейно
независимых векторов;2) любая система n
+ 1 векторов
линейно зависима.Обозначения : n =
dim V; ![]() .
.
58)
)Линейно зависимыми наз.ненулевые
векторы![]() нетривиальная
линейная комбинация которых равна
нулевому вектору:
нетривиальная
линейная комбинация которых равна
нулевому вектору:
![]()
59) Линейно независимыми наз.ненулевые векторы тривиальная линейная комбинация которых равна нулевому вектору.
60) Базис векторного пространства. Линейно независимая система векторов такая, что любой вектор пространства представляется в виде их линейной комбинации. В двумерном случае базис – это произвольная пара неколлинеарных векторов, в трехмерном случае – любая тройка некомпланарных векторов.
61 )Теорема о представлении вектора в виде линейной комбинации базисных векторов. Любой вектор из Rn можно единственным образом представить в виде линейной комбинации базисных векторов. Если векторы f1,f2,...,fn образуют базис пространства Rn , а x – любой вектор из Rn, то на основании теоремы x=α1f1+α2f2...+αnfn.(2) Правая часть (2) представляет собой линейную комбинацию векторов с коэффициентами.
62) Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.
63)Общим ур-нем прямой на плоскости наз.ур-не вида Ax + By + C (А2+В2 > 0).
64)Условия
перпендикулярности двух прямых:а) В
случае, когда прямые заданы уравнениями
![]()
![]()
![]()
![]()
![]()
![]() с угловым коэффициентом, необходимое
и достаточное условие их перпендикулярности
заключается в том, что их угловые
коэффициенты обратны по величине и
противоположны по знаку, т. е.
с угловым коэффициентом, необходимое
и достаточное условие их перпендикулярности
заключается в том, что их угловые
коэффициенты обратны по величине и
противоположны по знаку, т. е.![]()
![]()
![]()
65)Условия
параллельности двух прямых: а) Если
прямые заданы уравнениями
с угловым коэффициентом, то необходимое
и достаточное условие их параллельности
состоит в равенстве их угловых
коэффициентов:k1 = k2.б)
Для случая, когда прямые заданы уравнениями
в общем виде A1x + B1y + C1 =
0, A2x + B2y + C2 =
0 , необходимое и достаточное условие
их параллельности состоит в том, что
коэффициенты при соответствующих
текущих координатах в их уравнениях
пропорциональны, т.е.![]()
![]()
![]()
66)Общее уравнение плоскости. Любую плоскость можно задать уравнением плоскости первой степени вида Ах+Ву+Сz+D=0, где A, B и C не могут быть одновременно равны нулю.
67) Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.
68)
Условие
параллельности двух плоскостей.Две
плоскости α1 и
α2 параллельны
тогда и только тогда, когда их нормальные
векторы ![]() и
и ![]() параллельны,
а значит
параллельны,
а значит ![]() .Итак,
две плоскости параллельны друг другу
тогда и только тогда, когда коэффициенты
при соответствующих координатах
пропорциональн
.Итак,
две плоскости параллельны друг другу
тогда и только тогда, когда коэффициенты
при соответствующих координатах
пропорциональн![]() или
или ![]()
69)
Условие перпендикулярности плоскостей.
Две плоскости перпендикулярны тогда и
только тогда, когда их нормальные векторы
перпендикулярны, а следовательно, ![]() или
или ![]() .Таким
образом,
.Таким
образом, ![]() .
.
70)
Общее уравнение кривой второго порядка
имеет вид![]() Уравнение
такого вида может определять: 1) эллипс
(в частности, окружность), 2) гиперболу,
3) параболу, 4) пару прямых (параллельных,
пересекающихся либо совпадающих), 5)
точку или не определять никакой линии.В
простейшем случае, при В = 0, тип кривой
можно определить, выделив полные квадраты
переменных.
Уравнение
такого вида может определять: 1) эллипс
(в частности, окружность), 2) гиперболу,
3) параболу, 4) пару прямых (параллельных,
пересекающихся либо совпадающих), 5)
точку или не определять никакой линии.В
простейшем случае, при В = 0, тип кривой
можно определить, выделив полные квадраты
переменных.
71) Эллипсом называется
множество точек на плоскости, сумма
расстояний от каждой из которых до двух
заданных точек, называемых фокусами,
есть величина постоянная.Фокусы эллипса
обозначаются буквами ![]() и
и ![]() ,
расстояние между фокусами – через
,
расстояние между фокусами – через ![]() ,
а сумма расстояний от любой точки эллипса
до фокусов – через
,
а сумма расстояний от любой точки эллипса
до фокусов – через ![]() .
Причем 2a > 2c.Каноническое уравнение
эллипса имеет вид:
.
Причем 2a > 2c.Каноническое уравнение
эллипса имеет вид: ![]() , где
, где ![]() связаны между собой равенством a2 +
b2 =
c2 (
или b2 –
a2 =
c2).Величина
называется
большой осью, а
связаны между собой равенством a2 +
b2 =
c2 (
или b2 –
a2 =
c2).Величина
называется
большой осью, а ![]() –
малой осью эллипса.
–
малой осью эллипса.
72) Параболой
называется множество точек на плоскости,
равноудаленных от заданной точки
(называемой фокусом) и данной прямой
(называемой директрисой).Фокус
параболы принято обозначать буквой ![]() ,
директрису – буквой
,
директрису – буквой ![]() ,
расстояние от фокуса до директрисы –
буквой
,
расстояние от фокуса до директрисы –
буквой ![]() (p>0).Каноническое
уравнение параболы, фокус которой
расположен на оси абсцисс, имеет
вид
(p>0).Каноническое
уравнение параболы, фокус которой
расположен на оси абсцисс, имеет
вид ![]() или
или ![]() .
.
73) Гиперболой
называется множество точек плоскости,
разность расстояний от каждой из которых
до двух заданных (называемых фокусами)
есть величина постоянная. Эта постоянная
величина положительна и меньше расстояния
между фокусами. Фокусы гиперболы
обозначаются буквами ![]() ,
расстояние между фокусами – через
,
постоянную разность между расстояниями
от любой точки гиперболы до ее фокусов
– через
(2a<2с).Каноническое
уравнение:
,
расстояние между фокусами – через
,
постоянную разность между расстояниями
от любой точки гиперболы до ее фокусов
– через
(2a<2с).Каноническое
уравнение: ![]()
73.
гиперболой называется кривая, уравнением
которой в декартовой системе координат
имеет вид: ![]()
Гиперболой называется множество точек плоскости, абсолютной величиной разности ра
сстояний от которых до 2-х данных точек(фокусов гиперболы) постоянно.
Гипербола – это множество точек плоскости, отношение расстояний от которых до данной точки(фокусы гиперболы) и до данной прямой (одноименной с фокусом директрисы) есть величина постоянная, равная эксцентриситету гиперболы.
74. Окрестность точки А: И(а) называется любой интервал, содержащий точку А.
75.
![]() - окрестности точки х=х0
(И
(х0))
называется интервал (х-
;х+
)
- окрестности точки х=х0
(И
(х0))
называется интервал (х-
;х+
)
76.
проколотой
- окрестности точки х0-
![]()
77.
МножествоЕcR
называется ограниченным сверху, если
существует число b![]() R:
для любых х
Е → х≤b.
Где b
– верхняя грань множества Е.
R:
для любых х
Е → х≤b.
Где b
– верхняя грань множества Е.
78. Множество ЕcR называется ограниченным снизу, если существует число а R: для любых х Е → а<х. Где а – нижняя грань множества Е.
79.
Множество ЕcR
называется ограниченным, если оно
ограничено одновременно сверху и
снизу.
![]()
80. Число М называется точной верхней гранью множества Е. Если:
1.
![]()
2.
![]() ,
,
![]() – максимальная положительная величина
– максимальная положительная величина
M=supE=sup{x},x E
81.
m–
называется точной нижней гранью множества
Е![]() R,
если:
R,
если:
1.
![]()
2.
![]() ,
– максимальная положительная величина
,
– максимальная положительная величина
M=infE=inf{x},x E
82. Множество, не являющееся ограниченным, называется неограниченным.
83. если каждому натуральному числу n по некоторому закону поставлено в соответствии число аn, то говорят, что задана числовая последовательность {an}.
84. стационарная числовая последовательность – числовая последовательность {K},где К – фиксированное число.
85.
А называется пределом{an},
если для любого ![]() существует номер n:
существует номер n:
![]()
A=![]()
86.
Последовательность {an},
называется сходящейся существует
= А<![]() конечный
предел.
конечный
предел.
87. Последовательность {an}, называется расходящейся, если она не имеет конечного предела.
88.
Для сходимости числовой последовательности
необходимо и достаточно, чтобы
![]()
89. теорема о единственности пределов. Числовая последовательность не может иметь 2 и более пределов.
90.
Числовая последовательность {an}
называется ограниченной сверху, если
![]()
91.
Числовая последовательность {an}
называется ограниченной снизу, если
![]()
92.
Числовая последовательность {an}
называется ограниченной
![]()
93.
Числовая последовательность {an}
называется неограниченной ![]()
94.
Последовательность ![]() называется бесконечно
малой,
если
называется бесконечно
малой,
если ![]()
95.
Последовательность
называется бесконечно
большой,
если ![]() .
.
96. Теорема об ограниченности сходящейся последовательности. Любая сходящаяся числовая последовательность ограничена.
97.
Для существования предела A=
необходимо
и достаточно, чтобы ![]() ,
где
,
где![]() ,
,
![]()
98. Последовательность ![]() элементов
множества
элементов
множества ![]() называется неубывающей,
если каждый элемент этой последовательности
не превосходит следующего за ним.
называется неубывающей,
если каждый элемент этой последовательности
не превосходит следующего за ним.
—
неубывающая ![]()
99. Последовательность элементов множества называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
—
невозрастающая ![]()
100. Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают.
101. Теорема Вейерштрасса о пределе
монотонной ограниченной последовательности.Если
последовательность является возрастающей
и ограниченной сверху, то![]() (аналогично
для убывающей и ограниченной снизу
последовательности
(аналогично
для убывающей и ограниченной снизу
последовательности![]() )
)
102.
чило е:
![]()
103. Подпоследовательностью{an} последовательности {an} называется последовательность, все члены которой являются членами последовательности an.
104.Верхний
предел последовательности
![]() называется наибольший из всех частичных
пределов последовательности.
называется наибольший из всех частичных
пределов последовательности.
105.
Нижний
предел последовательности
![]() называется наименьший из всех частичных
пределов последовательности.
называется наименьший из всех частичных
пределов последовательности.
106. Теорема Больцмана-Вейерштрасса . Из всякой ограниченной последовательности можно выделить сходящуюся последовательность.
107.
Если ![]() по
закону fпоставлено
в соответствии число у
R,
то говорят, что на множестве Х задана
функция у=f(х).
по
закону fпоставлено
в соответствии число у
R,
то говорят, что на множестве Х задана
функция у=f(х).
108.
Предел функции по Коши.
Значение ![]() называется
предел функции
называется
предел функции ![]() в
точке
в
точке ![]() ,
если
,
если ![]()
![]() >0
>0
![]() : (
: (![]() :|x-x0|<0)
→
:|x-x0|<0)
→ ![]() любого сколько угодного малого числа
любого сколько угодного малого числа
![]() существует число
существует число ![]() .
.
109.
Предел функции по Гейне. Число Аназывается
![]() в
точке х0,
если
в
точке х0,
если ![]() :
:
![]() Ω;
xn=x0,
сходящейся в точке xn→x0при
n→
Ω;
xn=x0,
сходящейся в точке xn→x0при
n→![]() соответствия {f(xn)}:
f(x0)→A.
соответствия {f(xn)}:
f(x0)→A.
110.
Теорема о единственности пределов. Если
функция имеет![]() в
точке х0,
то он единственный.
в
точке х0,
то он единственный.
111.
функция называется ограниченной в
окрестности И(х0),
если для ![]() И(х0)
И(х0)
![]()
112.
Т.об ограниченности функции, имеющий
предел. Если f(x)
ограничена в И(х0)
и существует ![]() ,
то f(x)
ограничена в И(х0).
,
то f(x)
ограничена в И(х0).
113.
Теорема
о переходе к неравенству в
пределе.Еслиf(x)≤g(x)
для любых х в И(х0)
кроме быть может самой точки х0
существует
![]() , существует
, существует ![]() ,
то
≤
,
то
≤![]() .
.
114.
Теорема
о пределе промежуточной функции (правило
двух полицейских). Если любой х в И(х0)
кроме быть может х0,
![]() (x)≤f(x)≤g(x)
и существует
=
=
А, то существует
=А.
(x)≤f(x)≤g(x)
и существует
=
=
А, то существует
=А.
115.
Предел функции в бесконечности. Число
А называется
,
если ![]() существует
N,
то (если
существует
N,
то (если ![]() )
выполняется →|f(x)-A|<
)
выполняется →|f(x)-A|<![]() .
.
116.Функция
называется бесконечно
малой в окрестности точки
,
если ![]()
117.
Функция
называется бесконечно
большой в окрестности точки
,
если ![]()
118.
Функция
называется бесконечно
большой на бесконечности,
если ![]() либо
либо ![]()
119.
Теорема о связи между бесконечно
большой и бесконечно малой функциями:
Если функция ![]() -
функция бесконечно малая (
-
функция бесконечно малая (![]() ),
то функция
),
то функция ![]() есть
бесконечно большая функция и наоборот.
есть
бесконечно большая функция и наоборот.
120. односторонний
предел:A называют ![]()
121. Теорема о
связи односторонних пределов с пределом
функции (необходимое и достаточное
условие предела функции). Для существования
![]() н.и д., чтобы существовал
н.и д., чтобы существовал ![]() =f(x0-0);
существовал
=f(x0-0);
существовал ![]() =f(x0+0)
и f(x0-0)=f(x0+0).
=f(x0+0)
и f(x0-0)=f(x0+0).
122. f(x) непрерывной в точке x=x0: 1.существует f(x0); 2. Существует ; 3. =f(x0)
123.
Теорема об устойчивости знака непрерывной
в точке функции. Если f(x)
непрерывна в х=х0,
f(x0)![]() 0,
то существует
0,
то существует![]() (х0):
(х0):
![]() и сохраняет знак, как и число f(x0).
и сохраняет знак, как и число f(x0).
173 Определение горизонтальной асимптоты графика функции Пусть функция y=f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции lim f(x)=b . Тогда прямая y=b есть горизонтальная асимптота графика функции y=f(x) . 172 Определение наклонной асимптоты Пусть функция y=f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы lim f(x)/x=k и lim (f(x)-kx)=b. Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(x). Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет. Наклонная асимптота так же, как и горизонтальная, может быть односторонней. 171 Определение вертикальной асимптоты графика функции. Пусть функция y=f(x) определена хотя бы в некоторой полуокрестности точки x=a и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен -~ или +~. Тогда прямая x=a является вертикальной асимптотой графика функции. Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа)
170
Определение
асимптоты графика функции.
Асимптотой
графика функции y=f(x) называется прямая,
обладающая тем свойством, что расстояние
от точки (x,f(x)) графика функции до этой
прямой стремится к нулю при неограниченном
удалении точки графика от начала
координат.
169
Достаточные
условия перегиба графика функции.
1.
Если функция ![]() непрерывна в
точке
непрерывна в
точке ![]() и
имеет в этой точке конечную или бесконечную
производную и если
и
имеет в этой точке конечную или бесконечную
производную и если ![]() меняет
знак при переходе через точку
,
то точка
- точка
перегиба функции
.
меняет
знак при переходе через точку
,
то точка
- точка
перегиба функции
.
Вкратце:
первая производная
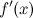 непрерывна
в окрестности точки
непрерывна
в окрестности точки 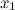 ;
;вторая производная
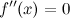 или
не существует в точке
;
или
не существует в точке
; при
переходе через точку
меняет
свой знак,
при
переходе через точку
меняет
свой знак,
тогда
в точке ![]() функция
функция ![]() имеет
перегиб.
имеет
перегиб.
168 Теорема о необходимом условии перегиба графика функции.
Если
точка
— точка
перегиба функции
и
если ![]() в
некоторой окрестности точки
(непрерывная
в точке
),
то
в
некоторой окрестности точки
(непрерывная
в точке
),
то ![]() .
.
167 Определение точки перегиба графика функции
Точка перегиба функции — это точка, в которой существует касательная к графику и существует такая окрестность точки , в которой график имеет разные направления выпуклости. (либо Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.)
166 Определение выпуклости графика функции вверх
График функции f(x) называется на интервале ( a, b ) выпуклым вверх если график у=f(x) лежит ниже любой касательной, проведенной к графику в этом интервале.
165 Определение выпуклости графика функции вниз
График функции f(x) называется на интервале ( a, b ) выпуклым вниз если график у=f(x) лежит выше любой касательной, проведенной к графику в этом интервале.
164 Теорема о достаточных условиях экстремума фоп.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:
Если производная
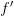 меняет
знак с «-» на «+» при переходе через
точку
:
меняет
знак с «-» на «+» при переходе через
точку
: 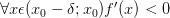 и
и 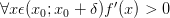 ,
то
—
точка строго минимума функции
,
то
—
точка строго минимума функции 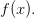
Если производная меняет знак с «+» на «-» при переходе через точку :
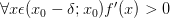 и
и 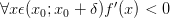 ,
то
—
точка строго максимума функции
,
то
—
точка строго максимума функции
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть
дана функция
,
ее первая производная ![]() и
пусть
и
пусть ![]() ,
тогда:
,
тогда:
Если
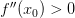 ,
то точка
—
точка строгого минимума;
,
то точка
—
точка строгого минимума;Если
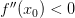 ,
то точка
—
точка строгого максимума.
,
то точка
—
точка строгого максимума.
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше 2х)
Пусть ![]() ,
, ![]() и
и ![]() ,
, ![]() Тогда:
Тогда:
Если
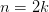 (т.е
(т.е 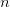 —
четное), то
—
точка экстремума:
—
четное), то
—
точка экстремума:если
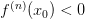 ,
то
—
точка локального максимума;
,
то
—
точка локального максимума;если
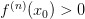 ,
то
—
точка локального минимума;
,
то
—
точка локального минимума;
Если
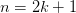 (т.е
—
нечетное), то
—
не является точкой экстремума.
(т.е
—
нечетное), то
—
не является точкой экстремума.
163 Теорема о необходимом условии экстремуме фоп.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции , то она критическая.
Доказательство
По
условию точка
—
точка экстремума функции
![]() по
теореме Ферма
производная
точка
является
критической.
по
теореме Ферма
производная
точка
является
критической.
162 Определение локального экстремума
По
определению функция ![]() достигает
в точке
достигает
в точке ![]() локального
максимума (минимума), если существует
окрестность этой точки
локального
максимума (минимума), если существует
окрестность этой точки ![]() ,
на которой выполняется неравенство
,
на которой выполняется неравенство
![]() (1)
(1)
(соответственно ![]() )
)
Локальный
максимум или минимум называется локальным
экстремумом (находится в окрестности
рассматриваемой точки.). Точка ![]() называется
точкой локального экстремума.
называется
точкой локального экстремума.
161 Определение локального минимума фоп
локальный минимум– это наименьшее значение функции в некоторой достаточно малой окрестности рассматриваемой точки.
называется точкой локального минимума функции
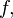 если
существует проколотая окрестность
если
существует проколотая окрестность 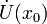 такая,
что
такая,
что
![]()
160 Определение локального максимума фоп
локальный максимум – это наибольшее значение функции в некоторой достаточно малой окрестности рассматриваемой точки.
называется точкой локального максимума функции если существует проколотая окрестность такая, что
![]()
159 Определение точки локального минимума фоп
Точка ![]() называется точкой
локального максимума функции
называется точкой
локального максимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности выполняется
неравенство:
из
этой окрестности выполняется
неравенство: ![]() .
.
158 Определение точки локального минимума фоп
Точка
называется точкой
локального минимума функции
,
если существует такая окрестность этой
точки, что для всех
из
этой окрестности ![]() .
.
157 Теорема о достаточных условиях возрастания (убывания) фоп в точке

156 Утверждение о достаточных условиях возрастания (убывания) фоп на отрезке
Определение возрастающей функции.
Функция y=f(x) возрастает
на интервале X, если для
любых ![]() и
и ![]() выполняется
неравенство
выполняется
неравенство ![]() .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение убывающей функции.
Функция y=f(x) убывает
на интервале X, если для
любых
и
выполняется
неравенство ![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
155 Определение монотонной фоп
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Функция строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.
154 Определение убывающей фоп
Функция называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.
![]()
153 Определение возрастающее фоп
Функция называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.
![]()
152 Определение неубывающей фоп
Функция
называется неубывающей
на промежутке, если из неравенства ![]() следует
неравенство
следует
неравенство ![]() .
.
151 Определение невозрастающей фоп
Функция
называется невозрастающей
на промежутке, если из неравенства
следует
неравенство ![]() .
.
150 Правило Лопиталя
-
метод нахождения пределов
функций, раскрывающий
неопределённости вида ![]() и
и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Пусть
функции
и ![]() удовлетворяют
следующим условиям:
удовлетворяют
следующим условиям:
1)
эти функции дифференцируемы в окрестности
точки ![]() ,
кроме, может быть, самой точки
;
,
кроме, может быть, самой точки
;
2) ![]() и
и ![]() в
этой окрестности;
в
этой окрестности;
3) ![]() ;
;
4) ![]() существует
конечный или бесконечный.
существует
конечный или бесконечный.
Тогда
существует и ![]() ,
причем
,
причем ![]()
Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.
149 Теорема Лагранжа (о конечных приращениях)
Пусть функция
непрерывна на отрезке
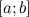 ;
;дифференцируема на интервале
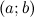 .
.
Тогда на интервале найдется по крайней мере одна точка , такая, что
![]()
148 Определение дифференциала высокого порядка
Дифференциалом ![]() -го
порядка
-го
порядка ![]() функции
называется
дифференциал от дифференциала
функции
называется
дифференциал от дифференциала![]() -го
порядка этой функции, то есть
-го
порядка этой функции, то есть
![]()
147 Определение производной высокого порядка
производная -го порядка функции есть первая производная от производной -го порядка этой функции:
![]()
146 Определение дифференциала функции
Дифференциалом
функции называется линейная
относительно ![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как ![]() или
или ![]() .
Таким образом:
.
Таким образом:
![]()
145 Теорема о дифференцируемости обратной функции
Пусть
функция ![]() определена
на промежутке Х, непрерывна,
монотонна (возрастает или убывает)
и дифференцируема наХ. Если ее
производная
определена
на промежутке Х, непрерывна,
монотонна (возрастает или убывает)
и дифференцируема наХ. Если ее
производная ![]() в
точке
в
точке ![]() не
равна нулю, то обратная
функция
не
равна нулю, то обратная
функция ![]() имеет
производную
имеет
производную ![]() в
точке
в
точке ![]() ,
причем
,
причем
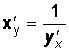 .
.
144 Теорема о дифференцируемости сложной функции
Если функция u(x) дифференцируема в точке x0, а функция y = f(u) дифференцируема в соответствующей точке u0 = u(x0), тогда сложная функция F(x) = f(u(x)) дифференцируема в точке x0, причем
|
F '(x0) = f '(u0) · u '(x0). |
|
143 Теорема о непрерывности дифференцируемой функции
Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).
Доказательство
Возьмем
произвольное фиксированное число x ![]() (a,b).
(a,b).
По условию теоремы
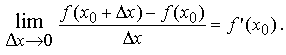
Следовательно,
в малой окрестности числа x0 можно
определить функцию α = α(Δx),
стремящуюся к нулю при ![]() такую,
что
такую,
что
![]()
Но
тогда ![]() и,
следовательно, функция f непрерывна
при x = x0. Так как
число x0 –
произвольное, то функция fнепрерывна
на всем интервале (a, b).
и,
следовательно, функция f непрерывна
при x = x0. Так как
число x0 –
произвольное, то функция fнепрерывна
на всем интервале (a, b).
Теорема доказана.
