Билет №10(2)

Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением, и получена деформацией сферы вдоль трёх взаимно перпендикулярных осей.

где — положительные параметры, удовлетворяющие неравенствам

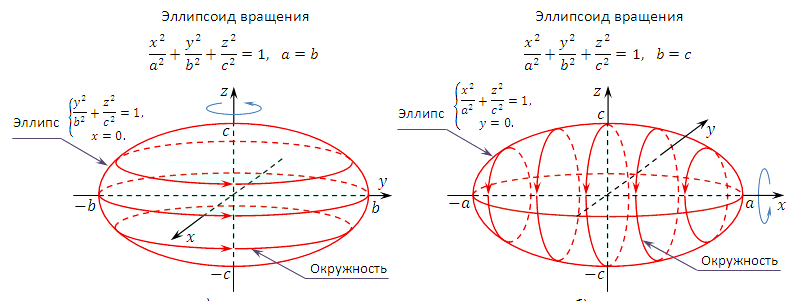
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при являются окружностями. Следовательно, сечения эллипсоида плоскостями представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси эллипс заданный в плоскости .

• Если 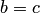, то все сечения эллипсоида (4.46) плоскостями при 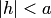будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси 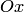эллипс

• Если все полуоси эллипсоида равны , то он представляет собой сферу 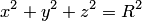радиуса 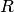, которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.

• Эллипсоид, у которого полуоси попарно различны , называется трехосным (или общим).

Эллипсоид обладает

• центральной симметрией относительно начала координат,

• осевой симметрией относительно координатных осей,

• плоскостной симметрией относительно начала координат.

Билет №11(2)

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

• если 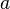и одного знака, то параболоид называется эллиптическим.

• если и разного знака, то параболоид называется гиперболическим.

• если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.

Эллипти́ческий параболо́ид — поверхность, задаваемая функцией вида

Эллиптический параболоид можно описать как семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.

Если то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.

Плоскость пересекает эллиптический параболоид по линии, имеющей в этой плоскости уравнение , которое равносильно уравнению параболы с фокальным параметром . Сечение параболоида плоскостью получаем, подставляя в уравнение: . Это уравнение равносильно уравнению параболы с фокальным параметром . Эти сечения называются главными параболами эллиптического параболоида

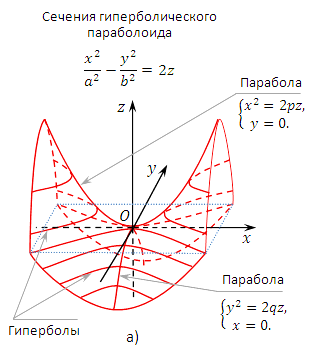
Гиперболи́ческий параболо́ид — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида

.

Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается с вершиной второй. Гиперболический параболоид является линейчатой поверхностью.