Билет №6(1)

Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек , и есть величина постоянная , бо́льшая расстояния между этими заданными точками Это геометрическое определение выражает фокальное свойство эллипса.

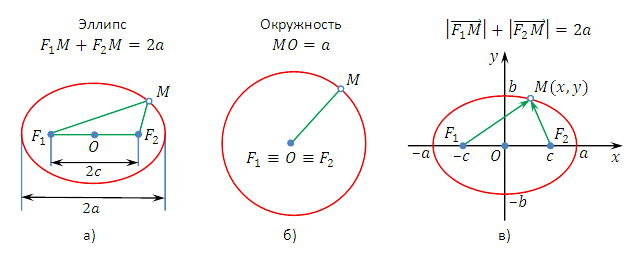
Точки , и называются фокусами эллипса, расстояние между ними — фокусным расстоянием, середина отрезка — центром эллипса, число — длиной большой оси эллипса (соответственно, число — большой полуосью эллипса). Отрезки и , соединяющие произвольную точку эллипса с его фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.

Отношение называется эксцентриситетом эллипса. Из определения следует, что . При , т.е. при , фокусы и , а также центр совпадают, и эллипс является окружностью радиуса .

К аноническое уравнение эллипса:

Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).

Эллипс с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство эллипса). Здесь и — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. или .

В самом деле, например, для фокуса и директрисы (рис.3.37,6) условие можно записать в координатной форме:

Уравнение эллипса в полярной системе координат (рис.3.37,в и 3.37(2)) имеет вид

Где фокальный параметр эллипса.

П араметрическое уравнение эллипса в канонической системе координат имеет вид

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и есть величина постоянная , меньшая расстояния между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Точки и называются фокусами гиперболы, расстояние между ними — фокусным расстоянием, середина отрезка — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки и , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение , где , называется эксцентриситетом гиперболы. Из определения следует, что .

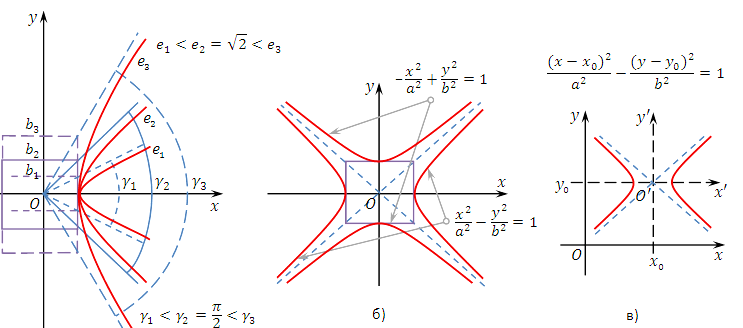
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

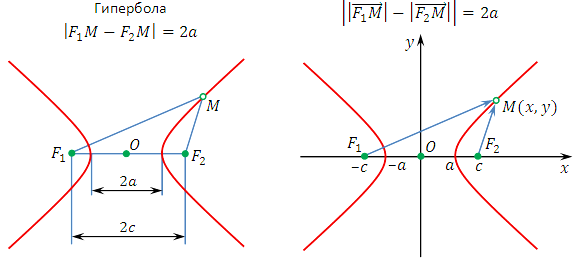
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и . Для произвольной точки , принадлежащей гиперболе, имеем:

Записывая это уравнение в координатной форме, получаем:

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

В самом деле, например, для фокуса и директрисы (рис.3.41,а) условие можно записать в координатной форме:

Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы.

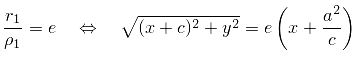
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид

, где — фокальный параметр гиперболы.

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

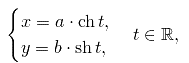
где — гиперболический косинус, a гиперболический синус.