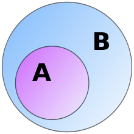
Пересечением множеств а и в называют новое множество х, содержащее те и только те элементы, которые входят и в множество а и в множество в. Пересечение множеств а и в обозначают или ab
Объединением называют множество Х,
состоящее из тех и только тех элементов,
которые входят хотя бы в одно из этих
множеств. Объединение двух множеств А
и В обозначают
.
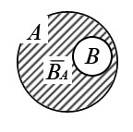
Разностью двух множеств А и
В называют такое множество
,
в которое входят все элементы из А,
не принадлежащие множеству В. При
этом не предполагается, что множество
В является частью множества А.
В случае, когда В – часть множества
А,
называют дополнением к В в
множестве А и обозначают
.
Симметрическая разность двух
множеств — теоретико-множественная
операция, результатом которой является
новое множество, включающее все элементы
исходных множеств, не принадлежащие
одновременно обоим исходным множествам.
Билет №5(1)
Элементарная комбинаторика имеет дело с множествами, из которых выбираются подмножества с определенными свойствами.
Набор
элементов x
,
…,
x
из множества Х = { x
,
…, x
} называется выборкой
объема m
из n
элементов.
Выборки называются упорядоченными, если порядок следования элементов в них задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.
Например, упорядоченные выборки ( x1, x5 ) и ( x5, x1 ) различные выборки объемом 2.
Если порядок следования элементов в выборке не является существенным, то такие выборки называются неупорядоченными
Размещением без повторений из m элементов называется упорядоченная выборка объемом m, в которой элементы различны.
Число
всех размещений без повторений объемом
m , составленных из n различных
элементов, обозначается через А
и вычисляется по формуле
А
= n·(n-1)· … ·(n - m + 1) =
Размещением с повторениями из m элементов называется упорядоченная выборка объемом m в которой элементы могут повторяться.
Число
всех
размещений с повторениями
объемом m,
составленных из nразличных
элементов, обозначается через
и
вычисляется по формуле
=
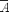n
.
Перестановкой из n элементов называется размещение без повторений объемом n.
Число всех перестановок из n элементов обозначается через Р и вычисляется по формуле
Р = n! = n·( n-1 )· … ·2·1.
Сочетанием без повторений из m элементов называется неупорядоченная выборка объемом m, в которой элементы различны.
Число всех различных сочетаний без повторений объемом m, которые могут быть составлены из n различных элементов обозначается через С и вычисляется по формуле
С
=
=
Граф — это совокупность непустого множества вершин и наборов пар вершин (связей между вершинами). Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.