Билет №4(1)

Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида , где и  — вещественные числа,  — мнимая единица; то есть . - действительная часть комплексного числа. - мнимая часть комплексного числа.

- Алгебраическая форма записи.

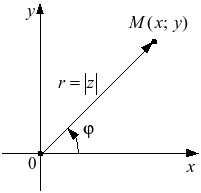
У гол между действительной осью и вектором называется аргументом комплексного числа : . Значение , заключенное в промежутке ,

- Тригонометрическая форма записи ,

- Показательная форма записи.

1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида

z = (x₁ + x₂, y₁ + y₂);

3) произведением комплексных чисел z₁ и z₂ называется комплексное число

z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

4) множество комплексных чисел , отождествляется с множеством действительных чисел R.

 Сравнение

означает, что и (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

 Сложение

 Вычитание

 Умножение

 Деление

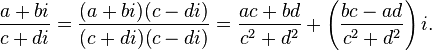
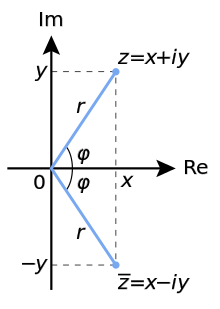Если комплексное число , то число называется сопряжённым. На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

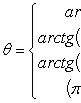
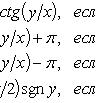
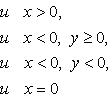
Формула Муавра для комплексных чисел утверждает, что … для любого

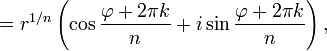
Билет № 7(2) «Множество есть совокупность различных элементов, мыслимая как единое целое»

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).

Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:

Пусто́е мно́жество — множество, не содержащее ни одного элемента. Ø Оно является подмножеством любого множества.

Числовые множества: (отрезок [a; b], полуотрезок [a; b), промежуток (a, b), числовой луч [a; +∞)).

• множество всех натуральных чисел ( );

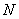• множество всех положительных рациональных чисел ( );

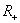• множество всех рациональных чисел( );

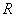• множество всех целых чисел ( );

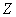• множество всех чисел, удовлетворяющих неравенству ;

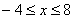• множество всех чисел вида 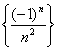, где n принимает все натуральные значения.

С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Второе - это множество его корней, т.е. чисел, при подстановке которых в уравнение оно обращается в тождество.