
- •Билет №1 (1) Билет №2 (1) Билет №3 (1)
- •Определители: (детерминанты)
- •Свойства определителей:
- •Билет №2(2)
- •Билет №4(1)
- •Пересечением множеств а и в называют новое множество х, содержащее те и только те элементы, которые входят и в множество а и в множество в. Пересечение множеств а и в обозначают или ab
- •Билет №5(1)
- •Билет №6(1)
- •Где фокальный параметр эллипса.
- •Билет №10(2)
- •Билет №7(1)
- •Окружность и треугольник
- •Окружность и многоугольники
- •Свойства:
Билет №2(2)
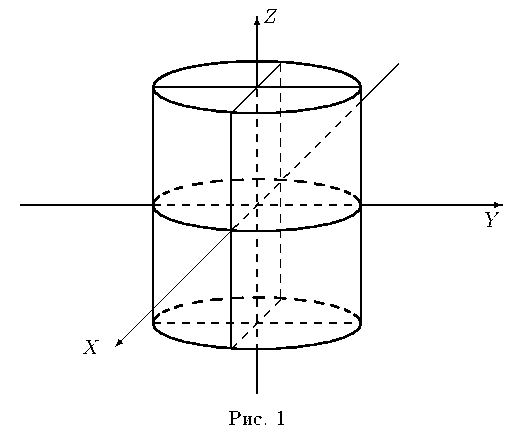
Поверхность называется цилиндрической, если она образована параллельным перемещением некоторой прямой, называемой образующей, вдоль некоторой кривой, называемой направляющей. Тело, ограниченное цилиндрической поверхностью, называют бесконечным цилиндром.
Теорема.
Если уравнение
![]() является
уравнением кривой на координатной
плоскости Оху, то это же уравнение
является уравнением цилиндрической
поверхности, направляющей которой
служит данная кривая, а образующей
является прямая, проходящая через точку
данной кривой и параллельной оси Оz.
является
уравнением кривой на координатной
плоскости Оху, то это же уравнение
является уравнением цилиндрической
поверхности, направляющей которой
служит данная кривая, а образующей
является прямая, проходящая через точку
данной кривой и параллельной оси Оz.
Цилиндрической поверхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:
F(x, y) = 0, F(x, z) = 0 или F(y, z) = 0 |
|
Если некоторая точка M0(x0, y0, z0) принадлежит цилиндрической поверхности, описываемой уравнением F(x, y) = 0 , то все точкипрямой, проходящей через эту точку параллельно оси OZ , также принадлежат цилиндрической поверхности. Такие прямые называются образующими цилиндрической поверхности, а кривая, описываемая уравнением F(x, y) = 0 и получающаяся в сечении любой плоскостью z = h , называется направляющей. |
|
Э
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1).
В Гиперболический цилиндр. Уравнение
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2).
Параболический цилиндр. Уравнение
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является парабола (рис. 3).
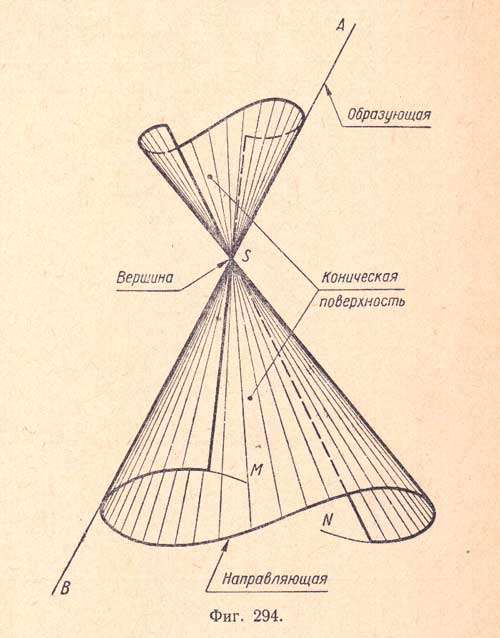
Б Конической поверхностью называется поверхность, образуемая движением прямой (AВ), перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку S и пересекает данную линию MN (фиг.294). Прямая АВ называется образующей, линия MN - направляющей, а точка S - вершиной конической поверхности. Каноническое уравнение круговой конической поверхности в декартовых координатах: Под действительным конусом второго порядка понимается поверхность второго порядка, которая задается этим уравнение:
|
Теорема:
Если
в некоторой декартовой
прямоугольной системе координат
поверхность
![]() задана
уравнением
задана
уравнением
![]() ,
где
,
где
![]() —
однородная функция, то
—
коническая поверхность с вершиной в
начале координат.
—
однородная функция, то
—
коническая поверхность с вершиной в
начале координат.
Если поверхность задана функцией , являющейся однородным алгебраическим многочленом второго порядка, то называется конической поверхностью второго порядка.

 ллиптический
цилиндр. Уравнение
ллиптический
цилиндр. Уравнение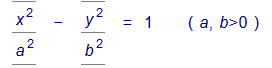
 частности, уравнение x2 + y2 =
R2 в трехмерном пространстве
определяет круглый цилиндр.
частности, уравнение x2 + y2 =
R2 в трехмерном пространстве
определяет круглый цилиндр.
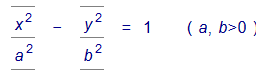

 илет
№3(2), Билет №4(2)
илет
№3(2), Билет №4(2)