Билет №1 (1) Билет №2 (1) Билет №3 (1)

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы естественным образом возникают при решении систем линейных уравнений.

Эта система состоит из линейных уравнений относительно неизвестных, может быть записана в виде следующего матричного уравнения вида: , где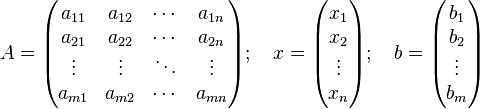

Матрица — это матрица коэффициентов системы линейных уравнений, вектор-столбец — вектор неизвестных, а вектор-столбец — некоторый заданный вектор.

Теорема Кро́некера — Капе́лли: (критерий совместности системы линейных алгебраических уравнений) Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Т.е ранг матрицы равен рангу расширенной матрицы .

Решение

что очевидным образом приводит к алгоритму вычисления значений неизвестных переменных по правилу Крамера.

Метод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем основной матрицы (причём для таких уравнений решение существует и единственно).

Назван по имени Габриэля Крамера (1704—1752), предложившего этот метод в 1750 г.

Пример:

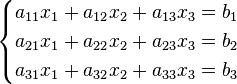
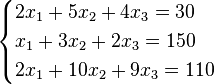
Определители: (детерминанты)

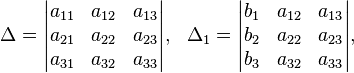
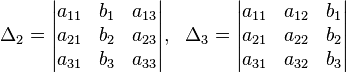
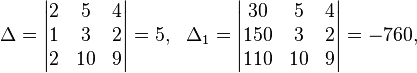
Решение:

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Пример:

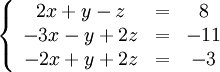
Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

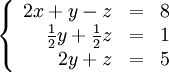
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

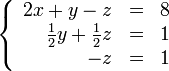
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма. На втором этапе разрешим полученные уравнения в обратном порядке.

из третьего;

из второго, подставив полученное

и з первого, подставив полученные и . Таким образом исходная система решена.

Метод треугольника:

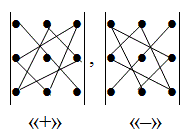
Разложение определителя по строке или столбцу:

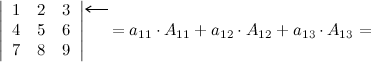
Действия с матрицами:

Вынесение (внесение) минуса из (в) матрицы(у).

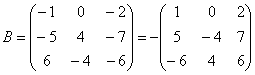
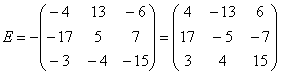
Умножение матрицы на число: Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число.

Транспонирование матрицы: Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

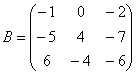
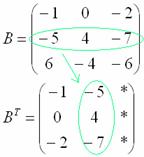
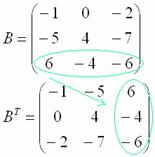
Сумма (разность) матриц: (должны быть одинаковыми по размеру) Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы. Таким же подобным образом происходит вычитание:

Умножение матриц: (Чтобы матрицу   можно было умножить на матрицу  нужно, чтобы число столбцов матрицы  равнялось числу строк матрицы .)

1 2

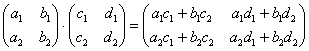
Нахождение обратное матрицы: (только для квадратных)

где  – определитель матрицы ,  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Находим определитель матрицы: (если определитель равен 0 – обратной матрицы не существует.

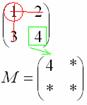
Находим матрицу миноров :

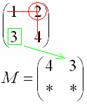
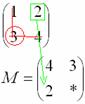
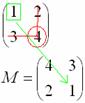
Находим матрицу алгебраических дополнений : (меняем знаки)

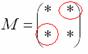
Находим транспонированную матрицу алгебраических дополнений :

Используем формулу: Проверка: А*А^(-1)=Е(единичная матрица)