4. Procenta

Z načí se %, většinou popisují poměr. Nebo přesněji kolik procent mají různé zastoupené složky nebo o kolik procent se změnil stav. Procenta představují jiný způsob,  jak vyjádřit část celku (setiny, tzn. zlomek) pomocí celého čísla.

Procenta obvykle označují nějakou relativní část z celku, přičemž celek jako takový se vyjádří jako 100 %. Název pochází z italštiny, per cento znamená ze sta. Při počítání s procenty si musíme vždy ujasnit, co je základ (100 %)!

Procenta se dají vždy přepsat do zlomku. Jedno procento se rovná jedné setině celku. Deset procent se rovná deseti setinám celku, neboli zkráceně jedné desetině. Padesát procent je padesát setin, zkráceně jedna polovina.

Zápis např. „45 %“ (45 procent) je ve skutečnosti jenom zkratkou pro zlomek , tzn. desetinné číslo 0,45.

K výpočtům procent se nejčastěji používá trojčlenka. Poměry hodnot se porovnávají jako u přímé úměrnosti.

Promile se nejčastěji používají při měření alkoholu v krvi řidiče. Někteří lidé se mylně domnívají, že promile je tisícina z procenta, ale to je chyba, pozor na to. Promile je tisícina z celku. Jinak se s promilí počítá úplně stejně jako s procenty. 1 ‰ = 0,001 základu

P říklad 7: Výpočet procentní části, známe-li základ a počet procent.

Urči DPH ve výši 19 % z částky 2 500 Kč.

Řešení:

1 00 % …………… 2 500 Kč

19 % …………….. x Kč

DPH činí 475 Kč.

P říklad 8: Výpočet základu (100 %), známe-li procentní část a počet procent.

Jaká byla původní cena televize, jestliže byla zlevněna o 20 % na 6 400 Kč?

Řešení:

(Sleva o 20 % znamená, že současná cena tvoří 80 % původní ceny!)

8 0 % …………… 6 400 Kč

100 % …………… x Kč

Původní cena televize byla 8 000 Kč.

 

P říklad 9: Výpočet počtu procent, známe-li základ a procentovou část.

O kolik procent byl automobil zdražen, jestliže jeho původní cena byla 420 000 Kč, a nyní stojí 460 000 Kč? 

Řešení:

4 20 000 Kč ……………. 100 %

460 000 Kč ……………. x %

109,5 % - 100 % = 9,5 %

Automobil byl zdražen o 9,5 %.

C vičení 4:

1. Kolik g tuku je obsaženo v 200 g sýra s deklarovaným 30% podílem tuku?

[60 g]

2. Po slevě o 10 % stojí boty 1 800 Kč. Jaká byla původní cena?

[2 000 Kč]

3. Ve firmě je 25 zaměstnanců, z toho 40 % žen. Kolik je ve firmě mužů a kolik žen?

[15 mužů; 10 žen]

4. Krevní zkouškou bylo zjištěno v krvi řidiče 0,6 ‰ alkoholu. Kolik je to gramů, je-li v těle přibližně 6 kg krve? [3,6 g]

5. Ze série 3 200 ručních hustilek bylo při kontrole zjištěno 16 vadných. Jaké procento představují vadné výrobky? [0,5 %]

4. Mocniny s přirozeným a celým exponentem

   1. Mocniny s přirozeným exponentem

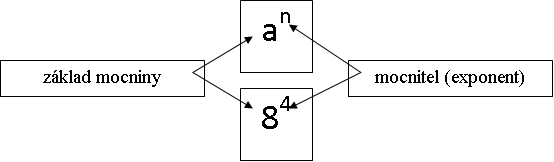
V matematice se snažíme o co nejstručnější zápisy. Součet 8 + 8 + 8 + 8 stručně zapíšeme jako součin 4 . 8. Podobně součin 8 . 8 . 8 . 8 stručně zapíšeme jako mocninu 8⁴. Současně používaný zápis mocnin byl zaveden francouzským matematikem a filozofem René Descartem v díle Géométrie, které vyšlo v roce 1637.

Definice mocniny: Pro každé reálné číslo a a každé přirozené číslo n je , kde v součinu na pravé straně je n činitelů.

Z definice vyplývá, že

1. pro každé reálné číslo a platí a¹ = a,

2. pro každé přirozené číslo n platí 1ⁿ = 1 a 0ⁿ = 0.

Zkoumáme-li, kdy je mocnina s přirozeným mocnitelem kladné a kdy záporné číslo, můžeme z definice přímo zapsat:

pro každé a  R a pro každé n  N platí:

1. je-li a > 0, pak aⁿ > 0,

2. je-li a < 0, pak a²ⁿ > 0,

3. je-li a < 0, pak a^2n-1 < 0.

V matematice, přírodních i technických oborech často pracujeme s velkými čísly, která zpravidla zapisujeme pomocí mocnin se základem 10, tj. ve tvaru , kde , n  N. Exponent n určíme tak, že zjistíme řád první platné číslice zapisovaného čísla.

Pravidla pro počítání s mocninami: Pro každá dvě reálná čísla a, b a pro každá přirozená čísla r, s platí:

P říklad 1:

Zapište ve tvaru , kde , n  N, následující číselné údaje:

1. Povodí Amazonky má rozlohu 6 900 000 km².

2. Rozloha Antarktidy je 13 000 000 km².

3. Výkon elektrárny dosáhl 1 320 000 000 W.

4. Čínská zeď má délku 8 800 km.

Řešení:

1. 6 900 000 = 6,9 . 10⁶

2. 13 000 000 = 1,3 . 10⁷

3. 1 320 000 000 = 1,32 . 10⁹

4. 8 800 = 8,8 . 10³

P říklad 2:

Vypočítejte:

Řešení:

P říklad 3:

Vypočítejte:

Řešení:

C vičení 1:

1. Vypočítejte:

2. Zjednodušte výraz a výsledek zapište pomocí celočíselných mocnin prvočísel: