2. Znaky dělitelnosti

Z naky dělitelnost čísel úzce souvisí s rozvinutým zápisem čísla v desítkové soustavě.

Přirozené číslo je dělitelné: 2: právě když je poslední číslice jeho zápisu dělitelná 2, 3: právě když je jeho ciferný součet dělitelný 3, 4: právě když jeho poslední dvojčíslí je dělitelné 4, 5: právě když jeho zápis končí nulou nebo pětkou, 9: právě když je jeho ciferný součet dělitelný 9, 10: právě když jeho zápis končí nulou, 6: právě když je dělitelné 2 a 3, 12: právě když je dělitelné 3 a 4, (nelze používat 6 a 2, protože jsou to soudělná čísla), 15: právě když je dělitelné 3 a 5, 18: právě když je dělitelné 2 a 9, (nelze používat 6 a 3, protože jsou to soudělná čísla).

P říklad 2:

U následujících čísel urči, zda jsou dělitelná některým z čísel: 2, 3, 4, 5, 6, 9, 10, 12 a 15:

.

Řešení:

a) 297

poslední cifra 7 není dělitelné 2, 4, 5, 6, 10, 12 a 15

ciferný součet 18 je dělitelné 3 a 9

b) 3 460

poslední cifra 0 dělitelné 2, 5, 10

poslední dvojčíslí 60 dělitelné 4

ciferný součet 13 není dělitelné 3 a 9 není dělitelné 6, 12 a 15

c) 3 162

poslední cifra 2 dělitelné 2; není dělitelné 5, 10, 15

poslední dvojčíslí 62 není dělitelné 4, 12

ciferný součet 12 je dělitelné 3  je dělitelné 6; není dělitelné 9

d) 70 010

poslední cifra 0 dělitelné 2, 5, 10

poslední dvojčíslí 10 není dělitelné 4, 12

ciferný součet 8 není dělitelné 3 a 9 není dělitelné 6, 12 a 15

e) 7 555

poslední cifra 5 dělitelné 5; není dělitelné 2, 4, 10, 12

ciferný součet 22 není dělitelné 3 a 9 není dělitelné 6, 15

f) 50 5984

poslední cifra 4 dělitelné 2, není dělitelné 5, 10, 15

poslední dvojčíslí 84 dělitelné 4

ciferný součet 31 není dělitelné 3 a 9 není dělitelné 6, 12

C vičení 2:

1. Doplňte vynechanou číslici tak, aby číslo bylo dělitelné čtyřmi. Uveďte všechny možnosti.

2. Doplňte vynechanou číslici tak, aby číslo bylo dělitelné devíti. Uveďte všechny možnosti.

3. Doplňte vynechanou číslici tak, aby bylo číslo dělitelné šesti. Uveďte všechny možnosti.

3. P rvočísla a čísla složená

Prvočísla jsou všechna přirozená čísla, která mají právě dva dělitele, číslo jedna a samo sebe. Složená čísla jsou všechna přirozená čísla, která mají aspoň tři různé dělitele. Číslo jedna není ani prvočíslo, ani číslo složené.

Složené číslo často potřebujeme vyjádřit ve tvaru součinu jeho dělitelů větších než jedna. Takovému vyjádření říkáme rozklad složeného čísla (např. ). Pokud rozložíme složené číslo na součin, ve kterém každý činitel je prvočíslo, říkáme tomuto rozkladu prvočíselný rozklad složeného čísla.

Způsoby, které nám umožní prvočíselný rozklad složeného čísla:

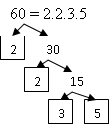
P říklad 3:

Proveďte prvočíselný rozklad čísla 60.

Řešení:

1. postupný rozklad:

2. stromeček:

3. t abulkový zápis („žebřík“):

60	2
30	2
15	3
5	5
1

V prvočíselném rozkladu jsme číslo 60 zapsali jako součin . Lze ho zapsat i stručněji užitím mocnin prvočísel: . Mocniny seřazujeme vzestupně, takto vytvoříme jednoznačný rozklad pro každé přirozené číslo  základní věta aritmetiky.

Základní věta aritmetiky: Každé přirozené číslo n > 1 lze zapsat jediným způsobem ve tvaru kde jsou prvočísla a jsou přirozená čísla.

C vičení 3:

1. Vypište prvočísla menší než 30.

2. Zapište prvočíselný rozklad daných čísel jako součin mocnin prvočísel: