2. Trigonometrie pravoúhlého trojúhelníku

Vypočítat pomocí Pythagorovy věty délku třetí strany pravoúhlého trojúhelníka, pokud znáte délky dvou stran, není problém. Teď si zopakujeme, jakým způsobem vypočítat velikost úhlu nebo délku některé strany pravoúhlého trojúhelníka, pokud znáte velikost jednoho úhlu a délku jedné strany. Tyto úlohy potřebovali už před tisíci lety řešit hvězdáři a zeměměřiči. Dnes se bez jejich řešení neobejdou také žádní technici - strojaři, stavbaři a další. Stačí, když využijete vašich znalostí o podobnosti pravoúhlých trojúhelníků.

Obrázek 8 – Podobnost trojúhelníka

Úseky AC, AC₁, AC₂ jsou shodné, pro názornost si zvolme velikost 100 m. Pravoúhlé trojúhelníky ABC, AB₁C₁, AB₂C₂ jsou podobné podle věty uu, platí tedy například rovnost poměrů délek odpovídajících stran:

V trojúhelnících ABC a AB₁C₁ je stejný také poměr délky protilehlé a přilehlé odvěsny:

Tento poměr délky protilehlé odvěsny ku délce přilehlé odvěsny se nazývá tangens úhlu α a zapisujeme:

Podobně lze ukázat, že jsou v pravoúhlých trojúhelnících se stejným úhlem α stále stejné i další poměry délek stran. Poměr délky protilehlé odvěsny ku délce přepony se nazývá sinus úhlu α, v našem trojúhelníku lze zapsat:

Poměr délky přilehlé odvěsny ku délce přepony se nazývá kosinus úhlu α, tedy:

Poměr délky přilehlé odvěsny ku délce protilehlé odvěsny se nazývá kotangens úhlu α, a píše se: .

Se změnou velikosti úhlu α se změní i hodnoty uvedených poměrů, každé velikosti úhlu přísluší jedna hodnota poměru. Jde tedy o funkce úhlu α, souhrnně nazvané goniometrické funkce.

G oniometrické funkce úhlu α pravoúhlého trojúhelníka: sinus: protilehlá : přepona kosinus: přilehlá : přepona tangens: protilehlá : přilehlá kotangens: přilehlá : protilehlá

P říklad 5:

Vyjádřete hodnoty sin β, cos β, tg β, cotg β podle obrázku:

Obrázek 9 – Obdélník

Řešení:

P říklad 6:

Vypočtěte velikost vnitřních úhlů pravoúhlého trojúhelníka ABC, jsou-li dány délky jeho stran: a = 5 cm a c = 8 cm.

Řešení:

Z definice funkce sinus vyplývá, že k výpočtu velikosti úhlu užijeme protilehlou odvěsnu a přeponu. Odvěsna a je protilehlá k úhlu α, proto můžeme počítat velikost úhlu α. Nejprve vyjádříme hodnotu sinus:

Ke známé hodnotě sinus pomocí tabulek určíme velikost odpovídajícího úhlu α:

.

Pro výpočet velikosti úhlu β máme několik možností. Využijeme tu nejjednodušší:

Velikost vnitřních úhlů daného trojúhelníka jsou

P říklad 7:

Jak daleko od břehu je bóje, která je z výšky 75 m nad hladinou jezera vidět pod hloubkovým úhlem 32°40´?

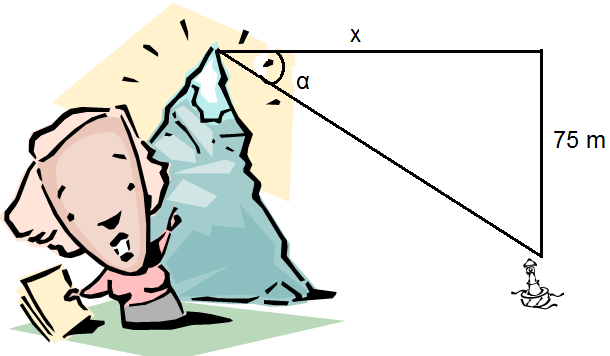
Obrázek 10 – Hloubkový úhel

Řešení:

nebo

Bóje je od břehu vzdálená 117 m.

Cvičení 2:

1. Vypočtěte velikost vnitřních úhlů kosočtverce se stranou délky 5 cm a jednou úhlopříčkou délky 8 cm. [α = 73°40´, β = 106°20´]

2. V obdélníku ABCD svírá úhlopříčka délky 6,4 cm s jednou stranou úhel α = 30°20´. Vypočtěte délky stran tohoto obdélníka. [a = 5,52 cm, b = 3,23 cm]

3. Rovnoramenný lichoběžník má ramena délky 5 cm a základny dlouhé 8 cm a 6 cm. Jak velké úhly svírají ramena se základnami? [78°30´]

4. Vypočtěte obsah pravidelného šestiúhelníka vepsaného do kružnice s poloměrem r = 5,3 cm. [7,6 cm²]

5. Pod jak velkým úhlem stoupá silnice, je-li na ní značka z obrázku:

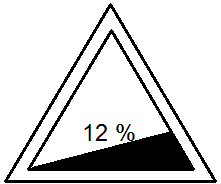[6°50´]