
Санкт-Петербургский государственный университет
Экономический факультет
Кафедра теории кредита и финансового менеджмента
Учебная группа студентов 1 курса магистратуры, программа «Финансы и учет», дневное отделение
Мисрокова Амина Нурбиевна
Индивидуальный проект по эконометрике
Преподаватель: Юдаева Мария Сергеевна
Работа представлена _________ ___________________
Оценка Подпись преподавателя
Санкт-Петербург
2011 г.
1.Исходные данные
В качестве исходных данных возьмем временные ряды, содержащие не менее 40 наблюдений
источник данных: база данных ММВБ;
тип данных – два индекса
частота – месяцы
Посмотрим на графики обоих временных рядов:
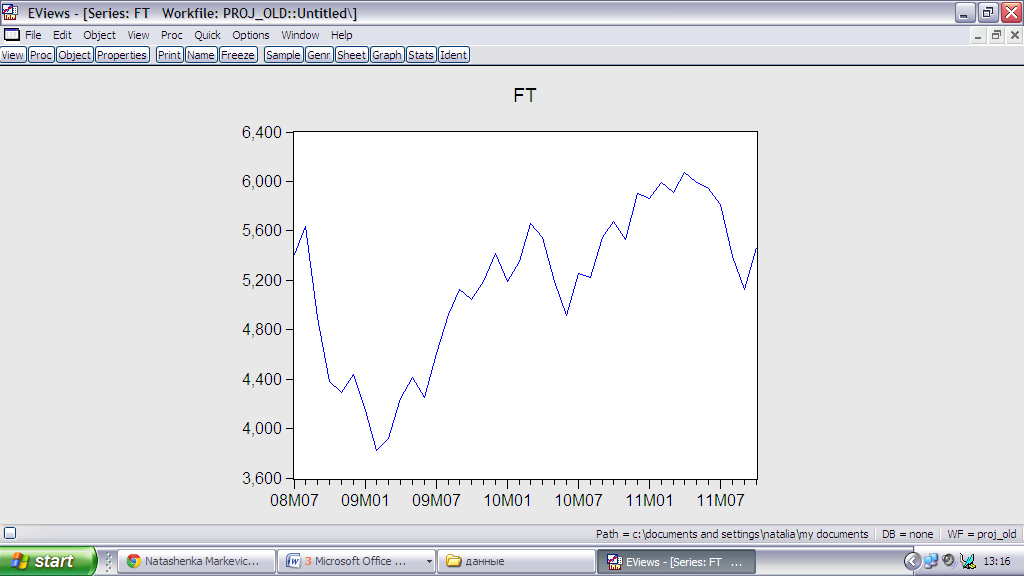
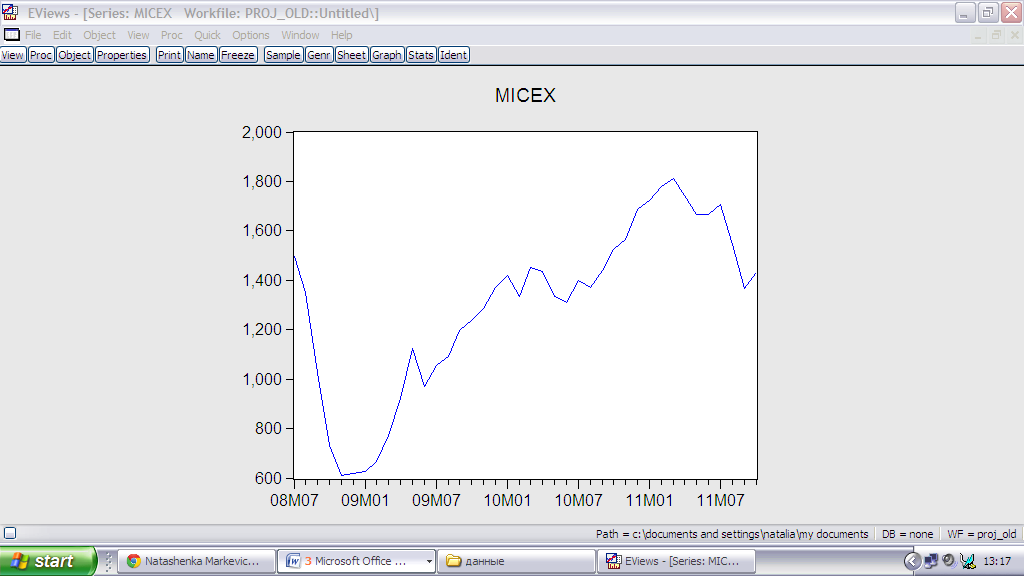
Можно сделать отметить схожесть графиков, основные тенденции на них одинаковые, поэтому можно предположить, что между ними может быть коинтеграция.
Мотивация
Наблюдая за котировками ценных бумаг, товаров, производных финансовых инструментов на мировых финансовых рынках (как на фондовом рынке, так и на валютном, долговом рынке и рынке капитала) становится, очевидно, что цены на биржевые инструменты движутся синхронно и сонаправленно. Среди научного сообщества, среди большинства крупных макроэкономистов нет единого мнения относительно причин подобной синхронизации системы глобальных финансов. Часть исследователей основой для этого считают неэкономические мотивы участников рынка: широко использующийся трейдерами арсенал инструментов технического анализа финансовых рынков (в том числе стратегии, построенные на зависимости между разными рынками и разными биржевыми инструментами, определяющие движение котировок «друг за другом»), психологические причины. Другие макроэкономисты видят в этом, прежде всего, чисто экономические причины: современный мир стал абсолютно глобальным, более того, весь мир превратился в открытое информационное пространство, любые события, происходящие в мировой экономике оказывают влияние на всю мировую финансовую систему. В этом глобальном мире нет места закрытым экономикам, независимым экономикам, любое макроэкономическое действие на каком-либо отдельном рынке перестает быть локальным событием этого рынка, оно оказывает влияние на мировую экономику, в этом основа глобализации. Так или иначе, очевидно, что между финансовыми рынками, фондовыми рынками разных стран существует определенная взаимосвязь; в своей работе, я постараюсь определить наличие и проанализировать характер взаимосвязи между рынками Великобритании и России. Итак, в данной работе я сравниваю данные индексов ММВБ (MICEX, наиболее ликвидный индекс РФ) и FTSE-100 (основной рыночный индикатор Великобритании, взвешенный по 100 крупнейшим компаниям британской экономики) ежемесячные данные, с июля 2008 по октябрь 2011 года.
Проверка порядка интегрируемости
Проверка ряда ft на порядок интегрируемости:
Построим уравнение следующего вида: ∆ln ft=α ln ft(t-1) + c + βt + εt
Для этого в комендной строке введем: ls d(ft) ft(-1) c @ trend
Нулевая гипотеза H0 состоит в том, что α=0, то есть единичный корень существует и ряд не стационарен, гипотеза H1 – в том, что α <0, единичный корень не существует и ряд стационарен.
H0: α=0
H1: α <0
Dependent Variable: D(FT) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 03:25 |
|
|
||
Sample (adjusted): 2008M08 2011M10 |
|
|||
Included observations: 39 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
FT(-1) |
-0.246624 |
0.093799 |
-2.629278 |
0.0125 |
C |
1033.746 |
417.7163 |
2.474758 |
0.0182 |
@TREND |
12.01973 |
5.211424 |
2.306419 |
0.0270 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.168162 |
Mean dependent var |
1.396410 |
|
Adjusted R-squared |
0.121949 |
S.D. dependent var |
272.4135 |
|
S.E. of regression |
255.2634 |
Akaike info criterion |
13.99627 |
|
Sum squared resid |
2345738. |
Schwarz criterion |
14.12424 |
|
Log likelihood |
-269.9273 |
Hannan-Quinn criter. |
14.04219 |
|
F-statistic |
3.638829 |
Durbin-Watson stat |
1.576109 |
|
Prob(F-statistic) |
0.036366 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Все коэффициенты значимы, так как их prob.<0,05, уровень значимости - 5%, c и @trend оставляем, так как они значимы
Проверяем на наличие автокорреляции с помощью Correlation LM Test:
Гипотезы:
H0: ρ1 = …=ρm=0 отсутствие автокорреляции
H1: наличие автокорреляции
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
0.929232 |
Prob. F(5,31) |
0.4755 |
|
Obs*R-squared |
5.083303 |
Prob. Chi-Square(5) |
0.4058 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 03:28 |
|
|
||
Sample: 2008M08 2011M10 |
|
|
||
Included observations: 39 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
FT(-1) |
-0.161646 |
0.162810 |
-0.992852 |
0.3285 |
C |
731.9019 |
730.1913 |
1.002343 |
0.3239 |
@TREND |
4.543629 |
6.695589 |
0.678600 |
0.5024 |
RESID(-1) |
0.310431 |
0.222762 |
1.393551 |
0.1734 |
RESID(-2) |
-0.005366 |
0.220338 |
-0.024354 |
0.9807 |
RESID(-3) |
0.168063 |
0.218335 |
0.769747 |
0.4473 |
RESID(-4) |
0.331894 |
0.208131 |
1.594640 |
0.1209 |
RESID(-5) |
0.042208 |
0.214624 |
0.196659 |
0.8454 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.130341 |
Mean dependent var |
2.55E-14 |
|
Adjusted R-squared |
-0.066033 |
S.D. dependent var |
248.4551 |
|
S.E. of regression |
256.5272 |
Akaike info criterion |
14.11303 |
|
Sum squared resid |
2039992. |
Schwarz criterion |
14.45427 |
|
Log likelihood |
-267.2040 |
Hannan-Quinn criter. |
14.23546 |
|
F-statistic |
0.663737 |
Durbin-Watson stat |
1.893187 |
|
Prob(F-statistic) |
0.700583 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как prob=0,4755, prob>0,05,мы не отвергаем H0, то есть автокорреляции нет.
∆ln ft=-0.246624ft(t-1) +1033.746+12.01973t+εt
Проведем проверку на порядок интегрируемости:
H0: есть единичный корень, ряд не стационарен
H1: нет единичного корня, ряд стационарен
Для этого сравним t-stat. (статистическое) и t-cr (расчетное)
Dependent Variable: D(FT) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 03:33 |
|
|
||
Sample (adjusted): 2008M08 2011M10 |
|
|||
Included observations: 39 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
FT(-1) |
-0.246624 |
0.093799 |
-2.629278 |
0.0125 |
C |
1033.746 |
417.7163 |
2.474758 |
0.0182 |
@TREND |
12.01973 |
5.211424 |
2.306419 |
0.0270 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.168162 |
Mean dependent var |
1.396410 |
|
Adjusted R-squared |
0.121949 |
S.D. dependent var |
272.4135 |
|
S.E. of regression |
255.2634 |
Akaike info criterion |
13.99627 |
|
Sum squared resid |
2345738. |
Schwarz criterion |
14.12424 |
|
Log likelihood |
-269.9273 |
Hannan-Quinn criter. |
14.04219 |
|
F-statistic |
3.638829 |
Durbin-Watson stat |
1.576109 |
|
Prob(F-statistic) |
0.036366 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tstat= -2.629278
Для нахождения расчетного значения используем Unit Root Test
Unit Root Test:
Null Hypothesis: FT has a unit root |
|
|||
Exogenous: Constant, Linear Trend |
|
|||
Lag Length: 0 (Fixed) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-2.629278 |
0.2703 |
||
Test critical values: |
1% level |
|
-4.211868 |
|
|
5% level |
|
-3.529758 |
|
|
10% level |
|
-3.196411 |
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation |
|
|||
Dependent Variable: D(FT) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 14:39 |
|
|
||
Sample (adjusted): 2008M08 2011M10 |
|
|||
Included observations: 39 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
FT(-1) |
-0.246624 |
0.093799 |
-2.629278 |
0.0125 |
C |
1033.746 |
417.7163 |
2.474758 |
0.0182 |
@TREND(2008M07) |
12.01973 |
5.211424 |
2.306419 |
0.0270 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.168162 |
Mean dependent var |
1.396410 |
|
Adjusted R-squared |
0.121949 |
S.D. dependent var |
272.4135 |
|
S.E. of regression |
255.2634 |
Akaike info criterion |
13.99627 |
|
Sum squared resid |
2345738. |
Schwarz criterion |
14.12424 |
|
Log likelihood |
-269.9273 |
Hannan-Quinn criter. |
14.04219 |
|
F-statistic |
3.638829 |
Durbin-Watson stat |
1.576109 |
|
Prob(F-statistic) |
0.036366 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tcr=-3.529758
Tstat > tcr=-3.529758, т е мы не отвергаем нулевую гипотезу о том, что единичный корень есть, ряд не стационарен.
Проверим первую разность на порядок интегрируемости:
В командной строке: ls d(ft,2) d(ft(-1)) c @trend
Dependent Variable: D(FT,2) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 15:31 |
|
|
||
Sample (adjusted): 2008M09 2011M10 |
|
|||
Included observations: 38 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.855128 |
0.167833 |
-5.095106 |
0.0000 |
C |
-68.75673 |
94.94777 |
-0.724153 |
0.4738 |
@TREND |
3.188158 |
4.082503 |
0.780932 |
0.4401 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.429065 |
Mean dependent var |
2.978421 |
|
Adjusted R-squared |
0.396441 |
S.D. dependent var |
354.9604 |
|
S.E. of regression |
275.7655 |
Akaike info criterion |
14.15264 |
|
Sum squared resid |
2661631. |
Schwarz criterion |
14.28192 |
|
Log likelihood |
-265.9001 |
Hannan-Quinn criter. |
14.19863 |
|
F-statistic |
13.15150 |
Durbin-Watson stat |
1.564267 |
|
Prob(F-statistic) |
0.000055 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Константа и тренд не значимы, их можно исключить:
Dependent Variable: D(FT,2) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 15:43 |
|
|
||
Sample (adjusted): 2008M09 2011M10 |
|
|||
Included observations: 38 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.849739 |
0.164477 |
-5.166302 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.419025 |
Mean dependent var |
2.978421 |
|
Adjusted R-squared |
0.419025 |
S.D. dependent var |
354.9604 |
|
S.E. of regression |
270.5569 |
Akaike info criterion |
14.06481 |
|
Sum squared resid |
2708438. |
Schwarz criterion |
14.10790 |
|
Log likelihood |
-266.2313 |
Hannan-Quinn criter. |
14.08014 |
|
Durbin-Watson stat |
1.546943 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение выглядит следующим образом:
∆2ln ft=-0.849739∆ln ft(t-1)+εt
Проверяем на автокорреляцию:
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
3.251605 |
Prob. F(5,32) |
0.0174 |
|
Obs*R-squared |
12.79813 |
Prob. Chi-Square(5) |
0.0253 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 15:58 |
|
|
||
Sample: 2008M09 2011M10 |
|
|
||
Included observations: 38 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-3.592439 |
1.045706 |
-3.435421 |
0.0017 |
RESID(-1) |
3.649391 |
1.044953 |
3.492397 |
0.0014 |
RESID(-2) |
0.386006 |
0.219073 |
1.761995 |
0.0876 |
RESID(-3) |
0.092166 |
0.159423 |
0.578119 |
0.5672 |
RESID(-4) |
0.250933 |
0.157264 |
1.595611 |
0.1204 |
RESID(-5) |
0.067482 |
0.161669 |
0.417408 |
0.6792 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.336793 |
Mean dependent var |
-3.359294 |
|
Adjusted R-squared |
0.233167 |
S.D. dependent var |
270.5355 |
|
S.E. of regression |
236.9052 |
Akaike info criterion |
13.91714 |
|
Sum squared resid |
1795971. |
Schwarz criterion |
14.17570 |
|
Log likelihood |
-258.4256 |
Hannan-Quinn criter. |
14.00913 |
|
Durbin-Watson stat |
2.129608 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Она есть, так как prob<0,05
Нам нужно избавиться от автокорреляции:
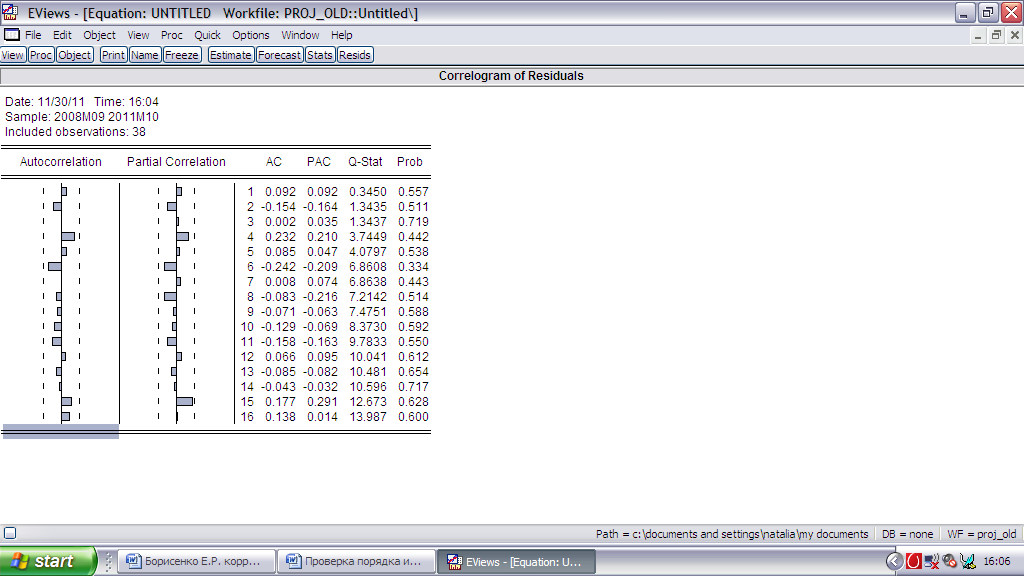 Можно
заметить, что 4-ый лаг выступает, поэтому
добавим его:
Можно
заметить, что 4-ый лаг выступает, поэтому
добавим его:
Dependent Variable: D(FT,2) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 16:42 |
|
|
||
Sample (adjusted): 2008M12 2011M10 |
|
|||
Included observations: 35 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.939595 |
0.169915 |
-5.529792 |
0.0000 |
D(FT(-4)) |
0.276776 |
0.147566 |
1.875609 |
0.0496 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.500619 |
Mean dependent var |
12.22000 |
|
Adjusted R-squared |
0.485487 |
S.D. dependent var |
321.0575 |
|
S.E. of regression |
230.2932 |
Akaike info criterion |
13.77203 |
|
Sum squared resid |
1750154. |
Schwarz criterion |
13.86091 |
|
Log likelihood |
-239.0105 |
Hannan-Quinn criter. |
13.80271 |
|
Durbin-Watson stat |
1.898778 |
|
|
|
|
|
|
|
|
|
|
|
|
|
проверяем на автокорреляцию:
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
0.157018 |
Prob. F(5,28) |
0.9761 |
|
Obs*R-squared |
0.406378 |
Prob. Chi-Square(5) |
0.9952 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 16:44 |
|
|
||
Sample: 2008M12 2011M10 |
|
|
||
Included observations: 35 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.558285 |
0.837822 |
-0.666353 |
0.5106 |
D(FT(-4)) |
0.061034 |
0.248961 |
0.245153 |
0.8081 |
RESID(-1) |
0.579644 |
0.867458 |
0.668209 |
0.5095 |
RESID(-2) |
-0.021663 |
0.208212 |
-0.104042 |
0.9179 |
RESID(-3) |
-0.004219 |
0.214590 |
-0.019659 |
0.9845 |
RESID(-4) |
-0.094201 |
0.331906 |
-0.283818 |
0.7786 |
RESID(-5) |
0.246957 |
0.314708 |
0.784718 |
0.4392 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.011611 |
Mean dependent var |
28.15031 |
|
Adjusted R-squared |
-0.200187 |
S.D. dependent var |
225.0763 |
|
S.E. of regression |
246.5780 |
Akaike info criterion |
14.03009 |
|
Sum squared resid |
1702420. |
Schwarz criterion |
14.34116 |
|
Log likelihood |
-238.5266 |
Hannan-Quinn criter. |
14.13747 |
|
Durbin-Watson stat |
1.963574 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Prob >0,05, значит автокореляции нет
Проверка порядка интегрируемости:
Dependent Variable: D(FT,2) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 17:55 |
|
|
||
Sample (adjusted): 2008M12 2011M10 |
|
|||
Included observations: 35 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.939595 |
0.169915 |
-5.529792 |
0.0000 |
D(FT(-4)) |
0.276776 |
0.147566 |
1.875609 |
0.0496 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.500619 |
Mean dependent var |
12.22000 |
|
Adjusted R-squared |
0.485487 |
S.D. dependent var |
321.0575 |
|
S.E. of regression |
230.2932 |
Akaike info criterion |
13.77203 |
|
Sum squared resid |
1750154. |
Schwarz criterion |
13.86091 |
|
Log likelihood |
-239.0105 |
Hannan-Quinn criter. |
13.80271 |
|
Durbin-Watson stat |
1.898778 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tstat=-5.529792
Null Hypothesis: D(FT) has a unit root |
|
|||
Exogenous: None |
|
|
||
Lag Length: 1 (Fixed) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-5.006388 |
0.0000 |
||
Test critical values: |
1% level |
|
-2.628961 |
|
|
5% level |
|
-1.950117 |
|
|
10% level |
|
-1.611339 |
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation |
|
|||
Dependent Variable: D(FT,2) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 17:56 |
|
|
||
Sample (adjusted): 2008M10 2011M10 |
|
|||
Included observations: 37 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(FT(-1)) |
-0.954181 |
0.190593 |
-5.006388 |
0.0000 |
D(FT(-1),2) |
0.208385 |
0.149817 |
1.390929 |
0.1730 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.461944 |
Mean dependent var |
28.97378 |
|
Adjusted R-squared |
0.446571 |
S.D. dependent var |
321.0992 |
|
S.E. of regression |
238.8747 |
Akaike info criterion |
13.84229 |
|
Sum squared resid |
1997139. |
Schwarz criterion |
13.92937 |
|
Log likelihood |
-254.0824 |
Hannan-Quinn criter. |
13.87299 |
|
Durbin-Watson stat |
2.094116 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tcr =1.950117 |
tstat=-5.529792 < tcr =-1.950117
нулевая гипотеза отвергается, единичного корня нет, ряд стационарен
Рассмотрим ряд mixec:
Уравнение, которое будем строить, выглядит следующим образом:
∆ln micext=αln micex(t-1) + c + βt + εt
В командной строке вводим следующую команду:
ls d(micex) micex(-1) c @trend
Dependent Variable: D(MICEX) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 18:12 |
|
|
||
Sample (adjusted): 2008M08 2011M10 |
|
|||
Included observations: 39 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
MICEX(-1) |
-0.250743 |
0.079840 |
-3.140574 |
0.0034 |
C |
173.2149 |
72.76702 |
2.380403 |
0.0227 |
@TREND |
7.465990 |
2.447360 |
3.050631 |
0.0043 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.229064 |
Mean dependent var |
-1.625897 |
|
Adjusted R-squared |
0.186235 |
S.D. dependent var |
115.6537 |
|
S.E. of regression |
104.3299 |
Akaike info criterion |
12.20680 |
|
Sum squared resid |
391850.5 |
Schwarz criterion |
12.33476 |
|
Log likelihood |
-235.0325 |
Hannan-Quinn criter. |
12.25271 |
|
F-statistic |
5.348255 |
Durbin-Watson stat |
1.110793 |
|
Prob(F-statistic) |
0.009254 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тренд и константа значимы, их оставляем
Проверяем на автокорреляцию:
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
3.128866 |
Prob. F(5,31) |
0.0212 |
|
Obs*R-squared |
13.08045 |
Prob. Chi-Square(5) |
0.0226 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 18:56 |
|
|
||
Sample: 2008M08 2011M10 |
|
|
||
Included observations: 39 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
MICEX(-1) |
-0.204357 |
0.098240 |
-2.080182 |
0.0459 |
C |
178.7639 |
90.41066 |
1.977244 |
0.0570 |
@TREND |
3.957633 |
2.434019 |
1.625966 |
0.1141 |
RESID(-1) |
0.522916 |
0.172537 |
3.030753 |
0.0049 |
RESID(-2) |
0.124254 |
0.198270 |
0.626690 |
0.5355 |
RESID(-3) |
0.235857 |
0.202314 |
1.165794 |
0.2526 |
RESID(-4) |
0.244161 |
0.203875 |
1.197603 |
0.2401 |
RESID(-5) |
-0.107446 |
0.199546 |
-0.538452 |
0.5941 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.335396 |
Mean dependent var |
2.92E-15 |
|
Adjusted R-squared |
0.185324 |
S.D. dependent var |
101.5473 |
|
S.E. of regression |
91.65598 |
Akaike info criterion |
12.05464 |
|
Sum squared resid |
260425.4 |
Schwarz criterion |
12.39589 |
|
Log likelihood |
-227.0655 |
Hannan-Quinn criter. |
12.17708 |
|
F-statistic |
2.234904 |
Durbin-Watson stat |
2.141518 |
|
Prob(F-statistic) |
0.058181 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Автокорреляция есть, так как prob<0,05
Попробуем добавить 1 и 2 лаги (2-ой лаг необходим для улудшения модели):
Dependent Variable: D(MICEX) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:41 |
|
|
||
Sample (adjusted): 2008M10 2011M10 |
|
|||
Included observations: 37 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
MICEX(-1) |
-0.286724 |
0.102606 |
-2.794433 |
0.0087 |
C |
223.7064 |
77.05813 |
2.903086 |
0.0066 |
@TREND |
7.403847 |
3.266059 |
2.266905 |
0.0303 |
D(MICEX(-1)) |
0.386478 |
0.147203 |
2.625480 |
0.0132 |
D(MICEX(-2)) |
0.166154 |
0.156901 |
1.058974 |
0.2975 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.338586 |
Mean dependent var |
10.92595 |
|
Adjusted R-squared |
0.255909 |
S.D. dependent var |
102.6485 |
|
S.E. of regression |
88.54531 |
Akaike info criterion |
11.92999 |
|
Sum squared resid |
250888.7 |
Schwarz criterion |
12.14769 |
|
Log likelihood |
-215.7049 |
Hannan-Quinn criter. |
12.00674 |
|
F-statistic |
4.095292 |
Durbin-Watson stat |
2.139889 |
|
Prob(F-statistic) |
0.008609 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверим на автокорреляцию
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
1.720308 |
Prob. F(5,27) |
0.1639 |
|
Obs*R-squared |
8.939415 |
Prob. Chi-Square(5) |
0.1115 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:44 |
|
|
||
Sample: 2008M10 2011M10 |
|
|
||
Included observations: 37 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
MICEX(-1) |
0.396890 |
0.394824 |
1.005233 |
0.3237 |
C |
-252.3407 |
287.4304 |
-0.877920 |
0.3877 |
@TREND |
-12.58253 |
10.48577 |
-1.199963 |
0.2406 |
D(MICEX(-1)) |
0.846731 |
0.660737 |
1.281494 |
0.2109 |
D(MICEX(-2)) |
-0.449218 |
0.576245 |
-0.779560 |
0.4424 |
RESID(-1) |
-1.453253 |
1.040366 |
-1.396867 |
0.1738 |
RESID(-2) |
-0.186172 |
0.389991 |
-0.477376 |
0.6369 |
RESID(-3) |
0.059590 |
0.429296 |
0.138809 |
0.8906 |
RESID(-4) |
0.431800 |
0.328492 |
1.314492 |
0.1997 |
RESID(-5) |
0.246590 |
0.268898 |
0.917040 |
0.3672 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.241606 |
Mean dependent var |
-1.20E-13 |
|
Adjusted R-squared |
-0.011192 |
S.D. dependent var |
83.48132 |
|
S.E. of regression |
83.94719 |
Akaike info criterion |
11.92371 |
|
Sum squared resid |
190272.5 |
Schwarz criterion |
12.35910 |
|
Log likelihood |
-210.5887 |
Hannan-Quinn criter. |
12.07721 |
|
F-statistic |
0.955727 |
Durbin-Watson stat |
2.072448 |
|
Prob(F-statistic) |
0.496023 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Авторорреляции нет, так как prob>0,05
Запишем полученное уравнение:
∆ln micex=-0.286724ln micex (t-1) + 0.386478∆ln micex(t-1)+ +0.166154∆ln micex(t-2)+ 223.7064+ 7.403847t
Порядок интегрируемости:
Проверим гипотезы:
H0: есть единичный корень, ряд не стационарен
H1: нет единичного корня, ряд стационарен
Null Hypothesis: MICEX has a unit root |
|
|||
Exogenous: Constant, Linear Trend |
|
|||
Lag Length: 2 (Fixed) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-2.794433 |
0.2082 |
||
Test critical values: |
1% level |
|
-4.226815 |
|
|
5% level |
|
-3.536601 |
|
|
10% level |
|
-3.200320 |
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation |
|
|||
Dependent Variable: D(MICEX) |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:45 |
|
|
||
Sample (adjusted): 2008M10 2011M10 |
|
|||
Included observations: 37 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
MICEX(-1) |
-0.286724 |
0.102606 |
-2.794433 |
0.0087 |
D(MICEX(-1)) |
0.386478 |
0.147203 |
2.625480 |
0.0132 |
D(MICEX(-2)) |
0.166154 |
0.156901 |
1.058974 |
0.2975 |
C |
223.7064 |
77.05813 |
2.903086 |
0.0066 |
@TREND(2008M07) |
7.403847 |
3.266059 |
2.266905 |
0.0303 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.338586 |
Mean dependent var |
10.92595 |
|
Adjusted R-squared |
0.255909 |
S.D. dependent var |
102.6485 |
|
S.E. of regression |
88.54531 |
Akaike info criterion |
11.92999 |
|
Sum squared resid |
250888.7 |
Schwarz criterion |
12.14769 |
|
Log likelihood |
-215.7049 |
Hannan-Quinn criter. |
12.00674 |
|
F-statistic |
4.095292 |
Durbin-Watson stat |
2.139889 |
|
Prob(F-statistic) |
0.008609 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tstat =-2.794433 >tcr = -3.536601, не отвергаем нулевую гипотезу – ряд не стационарен
Проверим порядок интегрируемости первой разности:
Наше уравнение должно выглядеть следующим образом:
∆2ln micext=αln micext-1 + c + βt + εt
Вводим в командной строке: ls d(micex,2) d(micex(-1)) c @trend
Dependent Variable: D(MICEX,2) |
|
|||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:50 |
|
|
||
Sample (adjusted): 2008M09 2011M10 |
|
|||
Included observations: 38 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(MICEX(-1)) |
-0.560274 |
0.149172 |
-3.755903 |
0.0006 |
C |
-3.062222 |
36.41269 |
-0.084098 |
0.9335 |
@TREND |
0.328622 |
1.566120 |
0.209832 |
0.8350 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.287927 |
Mean dependent var |
5.573421 |
|
Adjusted R-squared |
0.247238 |
S.D. dependent var |
121.2481 |
|
S.E. of regression |
105.1971 |
Akaike info criterion |
12.22521 |
|
Sum squared resid |
387325.2 |
Schwarz criterion |
12.35449 |
|
Log likelihood |
-229.2789 |
Hannan-Quinn criter. |
12.27120 |
|
F-statistic |
7.076147 |
Durbin-Watson stat |
1.951413 |
|
Prob(F-statistic) |
0.002625 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Убираем с и тренд, так как они не значимы:
Dependent Variable: D(MICEX,2) |
|
|||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:51 |
|
|
||
Sample (adjusted): 2008M09 2011M10 |
|
|||
Included observations: 38 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(MICEX(-1)) |
-0.557701 |
0.144290 |
-3.865130 |
0.0004 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.286083 |
Mean dependent var |
5.573421 |
|
Adjusted R-squared |
0.286083 |
S.D. dependent var |
121.2481 |
|
S.E. of regression |
102.4469 |
Akaike info criterion |
12.12253 |
|
Sum squared resid |
388328.4 |
Schwarz criterion |
12.16562 |
|
Log likelihood |
-229.3281 |
Hannan-Quinn criter. |
12.13786 |
|
Durbin-Watson stat |
1.952102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Наше уравнение будет выглядеть следующим образом:
∆2ln micext=-0.557701ln micext-1+ εt
Проверяем на автокорреляцию:
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
F-statistic |
2.390654 |
Prob. F(5,32) |
0.0596 |
|
Obs*R-squared |
10.29748 |
Prob. Chi-Square(5) |
0.0672 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
|
|
Dependent Variable: RESID |
|
|
||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:52 |
|
|
||
Sample: 2008M09 2011M10 |
|
|
||
Included observations: 38 |
|
|
||
Presample missing value lagged residuals set to zero. |
||||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(MICEX(-1)) |
1.869350 |
0.590860 |
3.163776 |
0.0034 |
RESID(-1) |
-2.064263 |
0.643274 |
-3.208997 |
0.0030 |
RESID(-2) |
-0.984379 |
0.321800 |
-3.058975 |
0.0045 |
RESID(-3) |
-0.356703 |
0.209567 |
-1.702097 |
0.0984 |
RESID(-4) |
-0.029786 |
0.175861 |
-0.169370 |
0.8666 |
RESID(-5) |
-0.140146 |
0.169048 |
-0.829035 |
0.4132 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.270986 |
Mean dependent var |
3.683256 |
|
Adjusted R-squared |
0.157078 |
S.D. dependent var |
102.3789 |
|
S.E. of regression |
93.99484 |
Akaike info criterion |
12.06830 |
|
Sum squared resid |
282720.9 |
Schwarz criterion |
12.32686 |
|
Log likelihood |
-223.2976 |
Hannan-Quinn criter. |
12.16029 |
|
Durbin-Watson stat |
2.104718 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Автокорреляции нет, так как prob>0,05
Порядок интегрируемости:
Null Hypothesis: D(MICEX) has a unit root |
|
|||
Exogenous: None |
|
|
||
Lag Length: 0 (Fixed) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-3.865130 |
0.0003 |
||
Test critical values: |
1% level |
|
-2.627238 |
|
|
5% level |
|
-1.949856 |
|
|
10% level |
|
-1.611469 |
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation |
|
|||
Dependent Variable: D(MICEX,2) |
|
|||
Method: Least Squares |
|
|
||
Date: 11/30/11 Time: 19:53 |
|
|
||
Sample (adjusted): 2008M09 2011M10 |
|
|||
Included observations: 38 after adjustments |
|
|||
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
D(MICEX(-1)) |
-0.557701 |
0.144290 |
-3.865130 |
0.0004 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.286083 |
Mean dependent var |
5.573421 |
|
Adjusted R-squared |
0.286083 |
S.D. dependent var |
121.2481 |
|
S.E. of regression |
102.4469 |
Akaike info criterion |
12.12253 |
|
Sum squared resid |
388328.4 |
Schwarz criterion |
12.16562 |
|
Log likelihood |
-229.3281 |
Hannan-Quinn criter. |
12.13786 |
|
Durbin-Watson stat |
1.952102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tstat=-3.865130 <tcr=-1.949856, значит ряд стационарен
Порядок интегрируемости:
ln ft~I(1)
ln micex~I(1)
Так у обоих рядов одинаковый порядок интегрируемости, то можно говорить, что в этом случае имеет место коинтграция
