Билет №7

1. Выбор и планирование факторов

При проведении эксперимента факторы должны отвечать следующим требованиям:

• 1.Независимость от других факторов.

• 2.Совместимость, т.е. возможность получения безопасных сочетаний факторов.

• 3.Управляемость, т.е. возможность получения определенного планом значения фактора.

• 4.Точность.

К ОДИРОВАНИЕ ФАКТОРОВ

• – кодированное значение фактора;

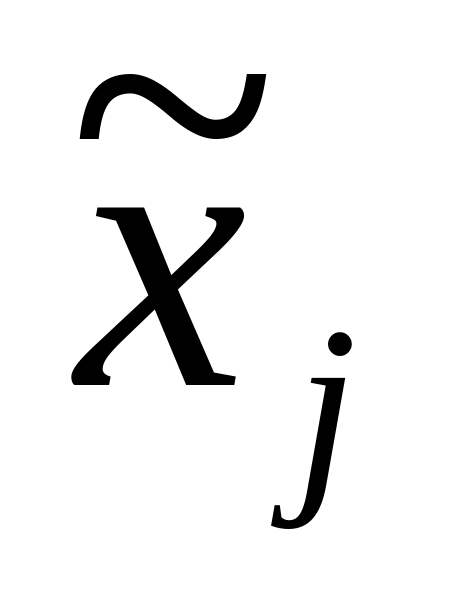
• – натуральное значение фактора;

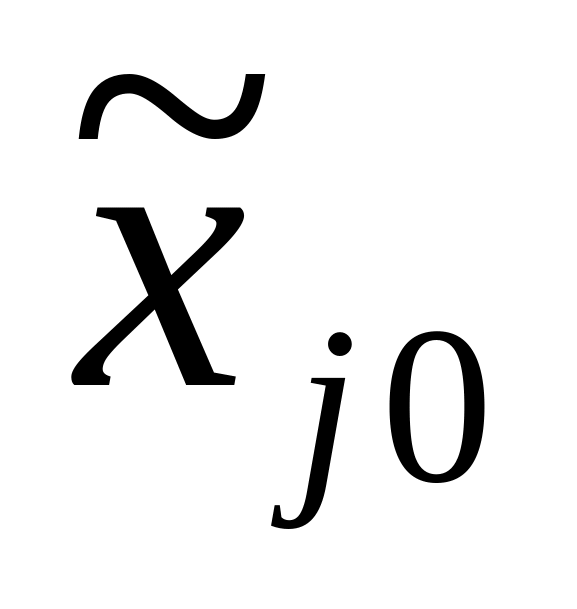
• – натуральное значение основного уровня;

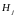• j – номер фактора;

– интервал варьирования.

• Основным или нулевым уровнем фактора называется то его значение, относительно которого фактор изменяется в процессе эксперимента:

X_j0 = 1/2 ( X_jв + X_jн ).

• Обычно факторы варьируются на двух уровнях, т. е. они принимают только два значения нижнее Х_jн и верхнее Х_jв или в кодированных единицах +1; -1. Такие эксперименты называют двух уровневыми.

• При кодировании факторов происходит переход от физической величины к ее изображению в относительных единицах.

2.ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ b_i

• Использование МНК, являющегося основой регрессионного анализа, возможно при трех допущениях:

• Отклик подчиняется нормальному закону распределения.

• Значения y_ui - статистически независимы.

• Построчные дисперсии однородны.

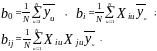
• С помощью указанных выражений получают статистически независимые коэффициенты b_i.

Билет №8.

1. ПОЛИНОМИАЛЬНАЯ МОДЕЛЬ

• Многофакторные эксперименты наиболее часто применяют для построения линейных по параметрам полиномиальных моделей. Вид полинома задается заранее, а его параметры определяются по экспериментальным данным.

• Ш 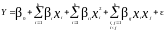ирокое распространение полиномиальных моделей объясняется тем, что исследуемые экспериментальными методами функции многих переменных f (х₁, х₂, . . . , х_к) в ограниченной области W обычно можно разложить в ряд Тейлора:

• где ₀, _i, _ij, _ii - действительные значения коэффициентов уравнения;

• х_i, x_j - факторы;

• Y - отклик;

•  - слагаемые третьего и более высокого порядка малости.

• Е 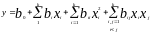сли модель включает в себя переменную (l - 1) степени, то данная переменная в эксперименте должна принимать не менее l значений или уровней.

• В уравнении регрессии коэффициенты b_i являются оценками соответствующих коэффициентов _i , а y - оценка отклика Y.

М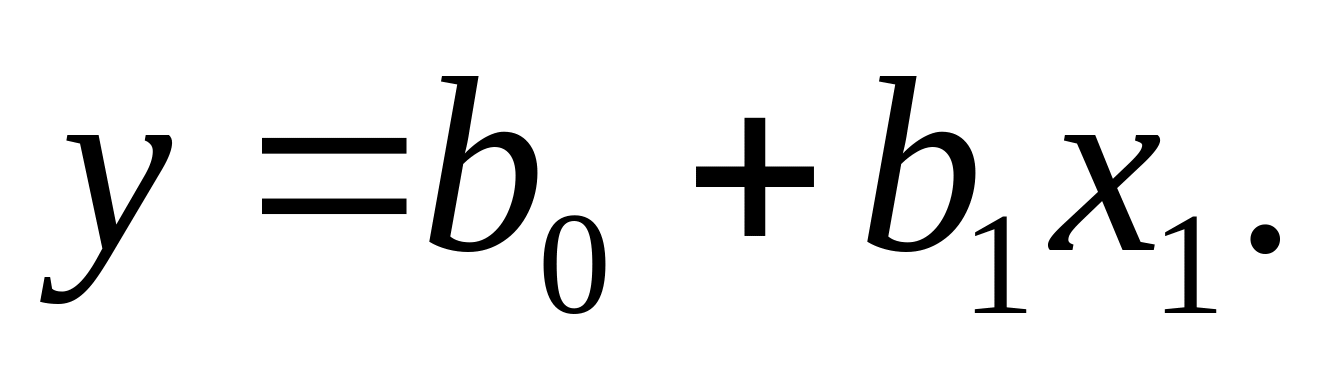 етод наименьших квадратов

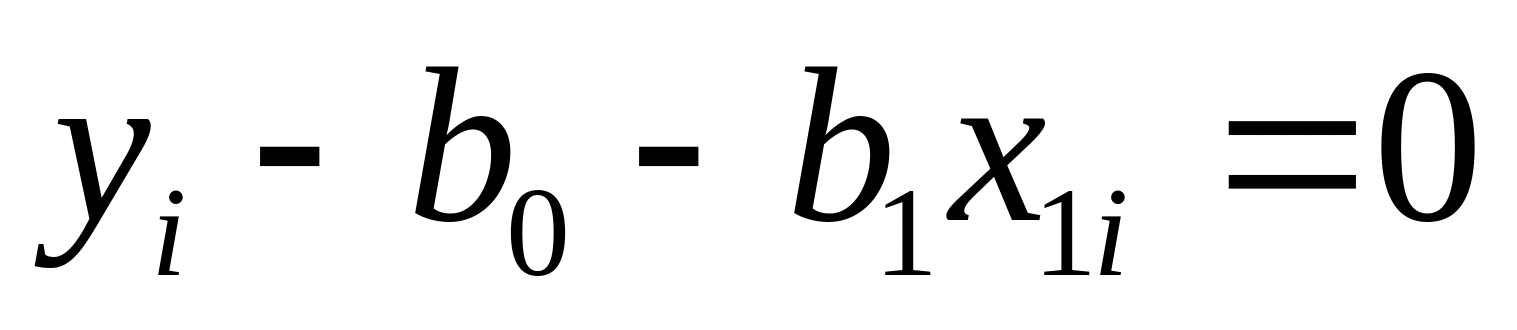
г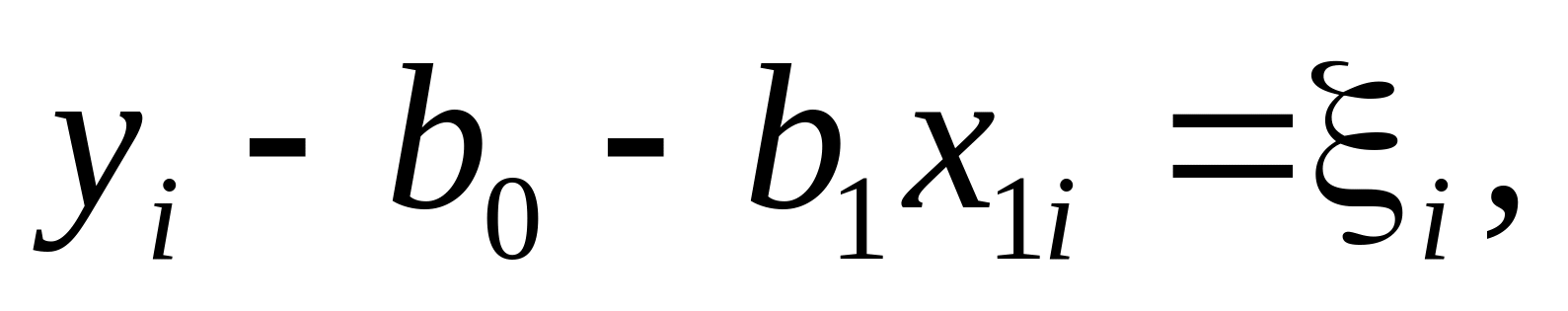 де i = 1, 2, ..., N – номер опыта.

где ξ_i – невязка, разность между экспериментальным и вычисленным по уравнению регрессии значениями у в i-й экспериментальной точке.

2.Дробный факторный эксперимент.

Билет №9

1.Полный факторный эксперимент

• Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

• Если в k – мерном пространстве фактор х₁ будет прини-мать l₁ уровень, фактор х₂ – l₂ уровней, а фактор х_к – l_к

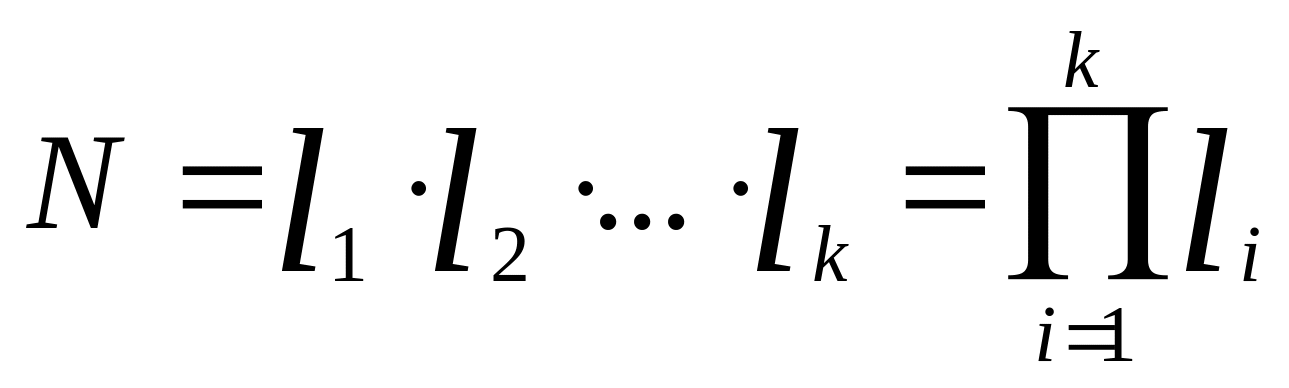
уровней, то k – факторов образуют:

наборов, или точек факторного пространства.

• В теории ТПЭ обычно l₁ = l₂ = . . . = l_k поэтому N = l^k. Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа

N = 2^k.

С войства матрицы ПФЭ типа 2k

• Симметричность относительно центра эксперимента,

где j – номер фактора, N – число опытов, j = 1, 2... k.

• Условие нормировки

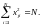
• Ортогональность матрицы планирования

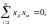
• j ≠ u, j, u= 0, 1, 2, …, k.

Параллельные опыты. Рандомизация

• Для снижения случайной составляющей погрешности в каждой точке плана производят по несколько параллельных опытов (обычно 3 - 5 ).

• В практике эксперимента встречаются случаи, когда отклик непроизвольно меняется под влиянием различных неконтролируемых воздействий. Они могут иметь как случайный так и периодический характер, причем период может быть меньше времени проведения эксперимента, так и значительно больше.

• Для уменьшения влияния медленно изменяющихся помех используют метод, или принцип, рандомизации.

• Термин “ рандомизация “ происходит от слова random (случай, случайность). Он означает, что опыты производятся не в той последовательности, как они записаны в плане, а в случайной последовательности.

• Кроме уменьшения влияния дрейфа, рандомизация обеспечивает статистическую независимость результатов опытов между собой. Поэтому принцип рандомизации имеет основополагающее значение в теории ПЭ и должен использоваться при проведении экспериментальных исследований.