23. Основные задачи, решаемые на основе контрольных уравнений

Основные задачи, решаемые на основе контрольных уравнений:

а) Обнаружение грубых ошибок измерения (плохих данных);

б) Сглаживание ошибок измерения (фильтрация);

в) Обнаружение ошибок в телесигналах о положении коммутационной аппаратуры;

г) Идентификация метрологических характеристических трактов получения измерительных данных.

23.1 Обнаружение грубых ошибок измерения (плохих данных)

Подставляя значения измеренных переменных в контрольное уравнение, получим невязки:

(т.к =0)

Априорная погрешность вектора измерения:

,

где М-матрица.

Обычно полагают, что эта матрица диагональная, т.е. погрешности двух измерений и некоррелированы (различны). Тогда:

,

где - дисперсия ошибки i- го измерения, задаваемая классом точности этого измерения.

Априорная дисперсия небаланса для q – го контрольного уравнения может быть записана в следующем виде:

,

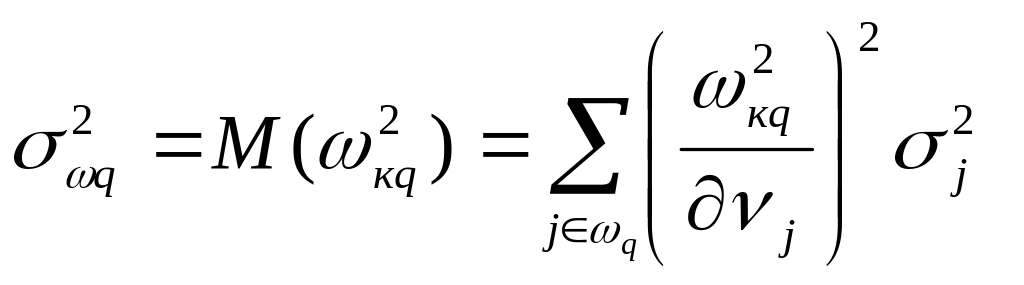где ω_q – множество индексов входящих в q-е контрольных уравнений измерений.

Процедура обнаружения грубых ошибок сводится к проверке статических гипотез, где нулевая гипотеза Н₀ следующая:

Невязка , полученная после подстановки в контрольное уравнение измеренных значений , принадлежит выборке . Если эта гипотеза не принимается, то значит измеренные значения с индексом содержат грубую ошибку.

Алгоритмы обнаружения грубых ошибок:

1. Вычислить невязки всех контрольных уравнений.

2. Измерение, входящее в контрольное уравнение с относительно малой невязкой, для которой выполняется условие:

,

объявляются достоверными, т.е. их точность считается составляющей априорным представлениям; достоверные измеренные величины вводятся в множество .

Контрольные уравнения, для которых выполнено это условие, исключаются из рассмотрения.

3. Из оставшейся системы контрольных уравнений выделяются подсистемы (если это возможно).

, такие, что

,

т.е., из этих подсистем можно определить некоторые непроверенные еще переменные на основе , уже объявленных достоверными.

Если таких подсистем не существует, то рассматриваем пункт 6.

4. Из подсистем вычисляем значения ; этими значениями замеряют измеренные значения , для которых разница велика (т.е это и есть грубые измерения).

Могут быть замечены и остальные негрубые измерения, но это существенно, т.к, для них эта разность мала. Переменные с их новыми значениями переводятся в вектор , уравнения исключают из рассмотрения.

5. Если остались нерассмотренные контрольные уравнения, то процесс повторяется с п.3. Если нет, то процесс закончен.

6. Если не удается из оставшихся контрольных уравнений выделить подсистемы, удовлетворяющие п.3, т.е. оставшиеся переменные считаются сомнительными, если они не могут быть рассчитаны на основе достоверных измерений.

Среди них есть содержащие грубые ошибки (иначе контрольные уравнения, в которые они входят, не имели бы большой невязки), но указать конкретно, какое измерение «виновато», можно лишь введя дополнительную информацию.

Как пример, для таких измерений просто увеличивается их априорная дисперсия, используемая затем для задания веса измерения в процедурах сглаживания.