21.2 Граничные переменные
Модели структурных элементов системы должны взаимодействовать друг с другом посредством переменных на границе. Кроме того, необходимо учитывать, что машины переменного тока моделируются в осях ДК. В результате этого получим:
Размеры всех матриц алгоритма 3 увеличатся в 3 раза;
Согласно алгоритму 3 рассчитываются сразу все потенциалы, указанные в двух координатах;
Матрицы инцидентности становятся блочными, если размер равен 2, то матрицы становятся диаграммами;
В системе, где имеется более двух генераторов, необходимо согласовать переменные;
Переход к действительным значениям тока и напряжения осуществляется по формулам вида:
.
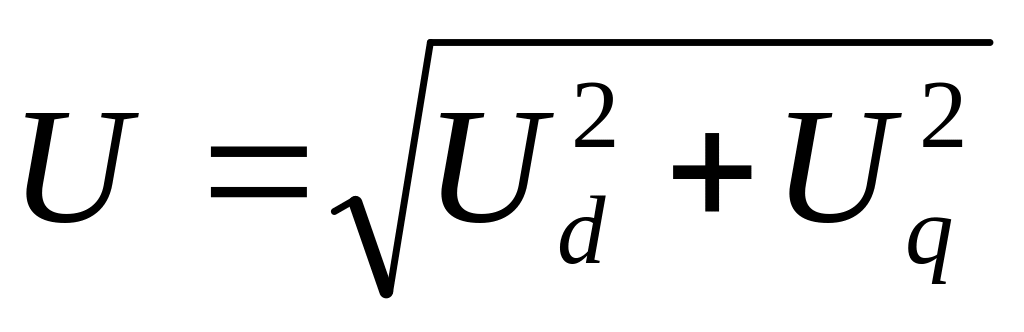Переход к мгновенным значениям осуществляется по формуле:
,
где
- матрица Горева:
Представление в осях d и q дает возможность использовать каталожные данные оборудования при моделировании АМ.
21.3 Представление модели элементов для моделирования системы
Модель линии электроприводов:
Модель трансформатора:
,
,
Модель комплексной статической нагрузки:
Линеаризованная модель асинхронного двигателя выводится из уравнения парка Горева:
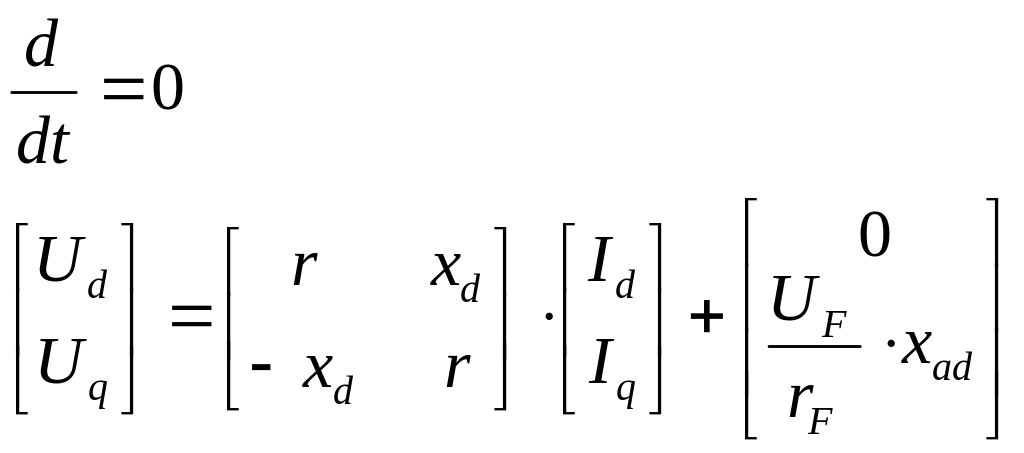
Линеаризованная модель синхронного двигателя также выводится из уравнения парка Горева:
21.4 Метод на основе Леммы об обратной матрице
Метод на основе Леммы об обратной матрице относится к экспрессному методу.
Методы лежат в основе многих АСДУ.
,
где
,
В аналоговом виде
можно представить матрицу проводимости
G в связи с изменением
схемы, например, при коммутации ветви
с проводимостью
между
узлами i и j
соответственно; на основании Леммы
можно записать:
,
где
,
Вектор-столбец соединений между узлами размерности n:
где
- вектор-столбец токов ветви, связывающий
узлы схемы с базисами;
- проводимость
ветви между узлами схемы и базисами.
Введем обозначения:
где
- вектор и скаляры, состоящие из элементов
матрицы узловых сопротивлений исходной
схемы;
- напряжение узлов
i, j исходного
режима.
Таким образом, получаем результат:
При изменении состояния узла, вызванных коммутациями нагрузки, необходимо воспользоваться информацией о режиме (вектор U) и обобщенных параметрах (матрица Z) исходной схемы. И сформировать вектор m, который кроме нуля будет включать только одну единицу, соответствующую позиции узла с изменяющимся состоянием.
22. Формирование модели текущего режима при оценке состояния системы энергоснабжения. Статические и динамические методы оценивания состояния
22.1 Формирование модели текущего режима при оценке состояния сэ
Основной задачей при формировании модели и топологии текущих режимов энергосистем является оценивание состояния системы.
Оценивание состояния при оперативном управлении может использоваться для повышения достоверности текущих телеизмерений и как информационная база для выполнения оперативных расчетов.
Вектор значений измеренных параметров представим в виде:
,
(1)
где
- получаемые данные, отличающие от
истинных (но неизвестных значений
);
-
величина отклонения от истинного
значения (погрешность).
Уравнение установившегося режима:
,
(2)
где
- неизменные параметры режима.
Инерция изменения параметров режимов во времени и наличие неслучайных составляющих в графиках позволяет выписать соотношения, связывающие значения параметров в смежные моменты времени.
Таким образом, с учетом инерции изменение во времени параметров режимов представим в виде:
,
(3)
где
- функция, известная или определенная
на основе обработки прошлых данных;
функция перехода от
момента времени к
-му
моменту времени;
- неустранимая
случайная составляющая, определяющая
возможную точность прогнозирования;
Уравнения динамики перехода состояния системы:
Статические (отбрасывается (3));
Динамические.