1. Найти область определения функции:

Р ешение:

Область определения данной функции ограничена условием неотрицательности подкоренного выражения под корнем чётной степени и отсутствием нуля в знаменателе степени:

То есть функция определена на интервале

Ответ:

2. Вычислить пределы:

а)

Решение:

Если в выражение под знаком предела подставить x=0, то получим неопределенность в пределе вида . Чтобы избавиться от неопределенности умножим числитель и знаменатель дроби на выражение сопряженное знаменателю, после чего свернем числитель по формуле разности квадратов :

Ответ:

б)

Решение:

Если в выражение под знаком предела подставить , то получим неопределенность в пределе вида . Чтобы избавиться от неопределенности, разделим каждое слагаемое числителя и знаменателя на x в наибольшей степени:

Ответ:

в)

Решение:

Если в выражение под знаком предела подставить x=0, то получим неопределенность в пределе вида . Чтобы избавиться от неопределенности будем использовать формулу первого замечательного предела , предварительно преобразовав выражение по формуле :

Ответ:

г)

Решение:

Для вычисления воспользуемся формулой второго замечательного предела , для этого предварительно преобразуем выражение:

Ответ:

3. Вычислить производные:

а)

Решение:

Для вычисления производной воспользуемся правилом производной произведения , производной сложной функции и основных элементарных функций:

б)

Решение:

Для вычисления производной воспользуемся правилом производной произведения , производной сложной функции и основных элементарных функций:

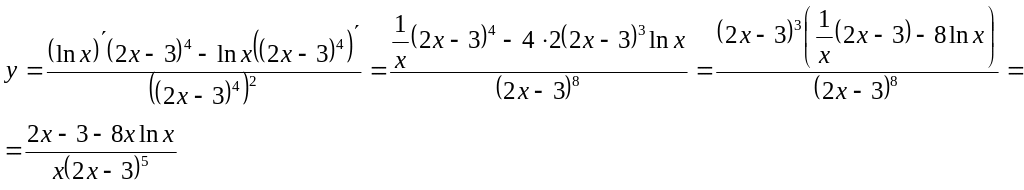
в)

Решение:

Для вычисления производной воспользуемся правилом производной алгебраической суммы и производной степенной функции:

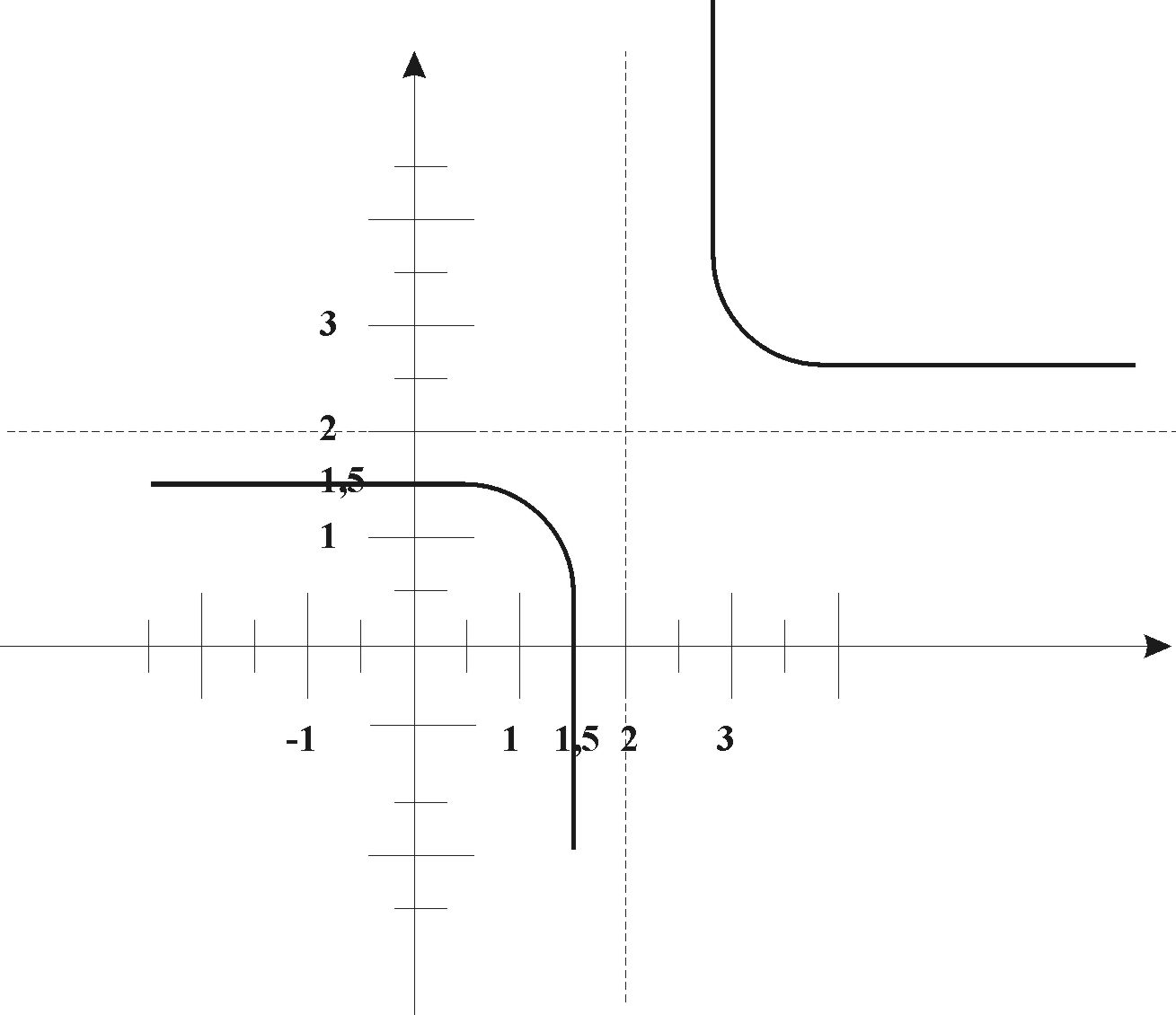
4. Исследовать функцию и построить ее график:

1. Область определения:

D(y) = R, кроме x=2, т. е.

2. Область значения:

E(y) = R, кроме y=2, т. е.

3. Четность, нечетность графика функции:

, т. е. функция общего вида.

4. Периодичность:

Функция непериодическая.

5. Точки пересечения с осями координат:

если x=0, то

если у=0, то

Итак, (0; 1,5)-точка пересечения с осью Оу,

(1,5; 0) – точка пересечения с осью Оx..

6. Непрерывность:

Функция не является непрерывной, x=2 – точка разрыва II рода.

7. Исследование на монотонность и точки экстремума:

Найдем первую производную:

X		2
	-	не сущ.	-
y	убывает	не сущ.	убывает

Функция монотонно убывает на всей области определения. Точек экстремума нет.

8. Исследование на перегиб:

Найдем вторую производную:

	(-; 2)	2	(2; +)
y"	-	не сущ.	+
y		не сущ.	

При x(-; 2) функция выпукла, при x(2;+) функция вогнута.

9. Исследование на асимптоты:

а) Вертикальные асимптоты:

x=2 - точка разрыва второго рода.

. Следовательно, x=2 - вертикальная асимптота.

б) Горизонтальные асимптоты:

. Следовательно, y=2 - горизонтальная асимптота.

в) Наклонная асимптота:

Следовательно, наклонных асимптот нет.

10. Дополнительные точки:

X	0	1	3	4	-1
Y	1,5	1	3	2,5	5/3

11. График функции: