1.Приведення параметрів розрахункової схеми до однієї ступені номінальної напруги

Расчетная схема энергосистемы содержит трансформаторные связи. Для создания эквивалентной электрической схемы замещения необходимо освободиться от трансформаторных связей, т.е. сопротивления и ЭДС схемы, находящиеся на разных ступенях трансформации, требуется привести к одной ступени, принятой за основную. Это приведение осуществляется по следующим соотношениям:

(2.15)

(2.16)

(2.17)

где   , … – коэффициенты трансформации, через которые величины (E, I, Z), подлежащие приведению, связаны со ступенью, к которой осуществляется приведение. Здесь под коэффициентом трансформации   трансформатора или автотрансформатора понимают отношение междуфазных напряжений холостого хода его обмоток в направлении от ступени, к которой осуществляется приведение параметров, к той ступени, на которой находятся величины, подлежащие приведению. При этом коэффициенты могут быть больше или меньше единицы.

2.Розрахунок замкненої електричної мережі методом Зейделя

Метод Зейделя оснований на тому, що уточнення на (і+1) ітерації напруги к-того вузла використовують зразу ж для обчислювання всіх наступних змінних. При цьому в якості першої ітерації приймається напруга, що дорівнює Uном.Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.

Итерации по методу Зейделя отличаются от простых итераций (10.12) тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1) -го приближения с меньшими номерами  . При рассмотрении развернутой формы системы итерационный процесс записывается в виде.

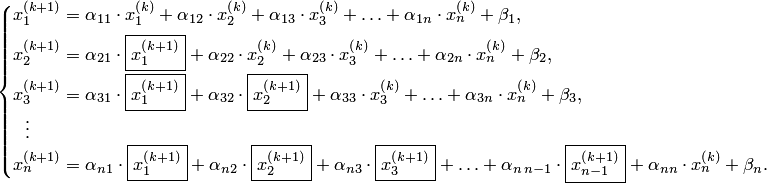
В каждое последующее уравнение подставляются значения неизвестных, полученных из предыдущих уравнений.

Теорема (10.3) о достаточном условии сходимости метода Зейделя. Если для системы   какая-либо норма матрицы   меньше единицы, т.е.  , то процесс последовательных приближений (10.15) сходится к единственному решению исходной системы   при любом начальном приближении  .

Записывая (10.15) в матричной форме, получаем

где   являются разложениями матрицы 

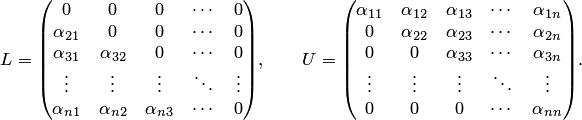
Преобразуя (10.16) к виду  , получаем матричную форму итерационного процесса метода Зейделя:

Тогда достаточное, а также необходимое и достаточное условия сходимости будут соответственно такими (см. теоремы 10.1 и 10.2):

1. Для обеспечения сходимости метода Зейделя требуется преобразовать систему   к виду   с преобладанием диагональных элементов в матрице а (см. метод простых итераций).

2. Процесс (10.15) называется последовательным итерированием, так как на каждой итерации полученные из предыдущих уравнений значения подставляются в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость, чем метод простых итераций (за счет накопления информации, полученной при решении предыдущих уравнений). Метод Зейделя может сходиться, если расходится метод простых итераций, и наоборот.

3. При расчетах на ЭВМ удобнее пользоваться формулой (10.16).

4. Преимуществом метода Зейделя, как и метода простых итераций, является его "самоисправляемость".

5. Метод Зейделя имеет преимущества перед методом простых итераций, так как он всегда сходится для нормальных систем линейных алгебраических уравнений, т.е. таких систем, в которых матрица   является симметрической и положительно определенной. Систему линейных алгебраических уравнений с невырожденной матрицей   всегда можно преобразовать к нормальной, если ее умножить слева на матрицу   (матрица   — симметрическая). Система  является нормальной.