Содержание

1. Введение в функциональное и логическое программирование…………5

1.1. Основные классы вычислительных моделей…………………………… 5

1.1.1 .Процедурная вычислительная модель……………………………… 6

1.1.2 Функциональная вычислительная модель………………………… .7

1.1.3.Логическая вычислительная модель…………………………………8

1.1.4 Объектно-ориентированная модель…………………………………8

1.2 . Методы оценки…………………………………………………………..9

1.3 . Обмен информацией в процессе оценки…………………………… …9

1.4.Понятие искусственного интеллекта……………………………………11

1.5. Символьные языки программирования и исчисление предикатов первого порядка…………………………………………………………………..11

1.6. Основные направления в искусственном интеллекте…………………14

1.7 . Подходы к построению искусственного интеллекта………………….15

2. Основы логического программирования………………………………….19

2.1. Основные понятия……………………………………………………. 19

2.2. Определение отношений на основе фактов и правил…………… ...20

2.3.Пример программы на языке Пролог………………………………...21

2.4. Использование рекурсии……………………………………………….25

2.5 Декларативная и процедурная трактовка программы………………..28

2.6. Структура программы…………………………………………………30

2.7 . Особенности логического программирования……………………...33.

2.8. Использование предиката not и квантификация переменных в

подцели с предикатом not...................................................................34.

3. Синтаксис Пролога…………………………………………………………..38

3.1. Объекты данных………………………………………………………38

3.2. Составные объекты и альтернативные домены………………………39

3.2.1. Составная структура……………………………………………...40

3.2.2. Доменная структурная диаграмма……………………………..41

3.2.3. Предикатная структурная диаграмма………………………….42

3.2.4. Альтернативные домены………………………………………....42

3.3. Сопоставление структур……………………………………………..44

3.4. Унификация и подстановки. Откат…………………………………45

3.5 Основные правила поиска с возвратом и пример на унификацию ...50

4. Принцип резолюции………………………………………...............................52

4.1. Логическое следствие …………………………………………………54

4.2 Логический вывод……………………………………………………....55

4.3. Преимущества и недостатки метода резолюции……………………57

4..4. Пример применения метода резолюции……………………………..59

5.. Управление поиском решения……………………………………………...61

5.1. Метод отката после неудачи………………………………………….62

5.2.Метод отсечения и отката……………………………………………..64

5.2.1. Влияние предиката cut на составную цель……………………64

5.2.2. Влияние предиката cut на процедуру………………………….65

5.2.3. Использование зеленых и красных отсечений………………..68

5.2.4. Использование предиката not как средства управления. ……..71.

5.3. Метод повтора, определяемый пользователем………………………71

5.4. Методы организации рекурсии………………………………………. 76

6. Работа со списками………………………………………………………....84

6.1. Операции над структурами типа список………………………………87

6.2 .Предикат findall и его использование…………………………………97

6.3 . Операции со структурами данных…………………………………….98

Литература………………………………………………………………………..101

1.Введение в функциональное и логическое программирование

“ Программирование - это

одно из наиболее сложных

направлений математики”

Дейкстра

“Границы моего языка –

границы моего мира”

Людвиг Виттгенштейн

1.1. Основные классы вычислительных моделей

Курс посвящен изучению логического и функционального программирования.

Современным программистам предлагаются различные стили программирования (парадигмы).

Внутри каждого из этих стилей имеются свои наборы различных языков.

В программировании термин парадигма используется для определения модели вычислений, то есть способа структурирования информации, организации вычислений и данных.

Для описания процесса вычислений используются четыре основных типа таких моделей: процедурная, функциональная, логическая и объектно-ориентированная.

Поставленная перед разработчиком задача обычно имеет некоторый набор исходных данных и цель. Это отражается в постановке задачи. Если поставленная задача решается на компьютере, то возникает проблема формализации этой задачи, так как вычислительный процесс может быть выполнен на компьютере только в том случае, если он формализован. В основу вычислительного процесса могут быть положены разные математические формализмы (вычислительные модели). Четыре основных парадигмы программирования представлены на рис.1.1.

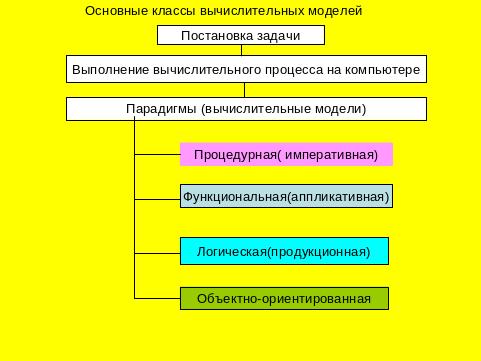
Рис. 1.1. Различные стили программирования

1.1.1 Процедурная вычислительная модель

В этой модели алгоритм (программа) в явном виде (с помощью выполняемых операторов присваивания) определяет как сами действия, так и последовательность их выполнения ( С, С++, Pascal, Ada и другие языки программирования) Концепция памяти – преобразование исходного состояния памяти (значения переменных) в заключительное состояние. Фон-неймановские машины состоят из ячеек памяти и процессора, имеющего локальную память в виде регистров. Компьютер работает на ограниченном множестве операций, и программист вынужден мыслить в терминах этого ограниченного множества операций.

1.1.2 Функциональная вычислительная модель

В этой модели программа рассматривается как множество определений функций. Отличительной чертой этих моделей является то, что в основу их положена математическая модель, называемая “лямбда-исчислением” Черча. Для представления обычной функции используется выражение f(x).При этом неясно: то ли оно означает функцию f,то ли ее значение при заданном параметре x. Для четкого описания функции было введено выражение xf(x).То есть, когда хотят рассматривать выражение P как функцию от x, следует использовать запись xP (лямбда-абстракция). Таким образом, выражение x(x+y) является функцией от x, а не от у. При этом x называют связанной переменной, а y- свободной переменной.

Таким образом, главным в парадигме функционального программирования является понятие функции (отсюда и название – функциональное программирование). Математики придумали множество теоретических и практических аппаратов для оперирования функциями (дифференцирование, интегрирование, функциональный анализ, теория нечетких множеств и т.д.) Теперь появился раздел, который напрямую связал математическую теорию функций и технологию создания программного обеспечения (ПО) для компьютеров. Математические функции выражают связь между параметрами (входом) и результатом (выходом) некоторого процесса. То есть, функцию можно рассматривать как некоторый черный ящик, входные значения которого порождают значения на выходе (выражают связь между входом и выходом некоторого процесса). Так как вычисление – это тоже процесс, имеющий вход и выход, то функция является вполне адекватным средством описания вычислений. Именно этот простой принцип и положен в основу функциональной парадигмы и функционального программирования. Функции определяются через другие функции или рекурсивно – через самих себя. В процессе выполнения программы функции получают параметры, вычисляют и возвращают результат, в случае необходимости вычисляя значения других функций. Все, что необходимо сделать программе для получения желаемого результата при решении задачи, должно быть представлено в виде системы взаимосвязанных функций.