2.1. Определение параметров элементарной ячейки кристаллических материалов Термины и определения

Кристаллическая решетка – пространственное периодическое расположение атомов (ионов, молекул) в кристаллическом веществе, являющееся геометрическим образом представления о кристаллическом строении

Узлы кристаллической решетки – точки кристаллической решетки, в которых расположены атомы или ионы

Кристаллографические (атомные) плоскости – плоскости, проходящие через три узла кристаллической решетки

Элементарная ячейка – параллелепипед, построенный на узлах кристаллической решетки и представляющий собой минимальный объем, отражающий все особенности кристаллического вещества, параллельные переносы (трансляции) которого в трех измерениях позволяют построить всю кристаллическую решетку

Параметры элементарной ячейки – величины образующих ее ребер - a, b и c (периоды ячейки) и три угла между ними — α, β и γ.

Введение

Точное определение параметров элементарной ячейки имеет большое практическое значение при изучении состава, структуры и физико-химических свойств многих кристаллических материалов, особенно металлов и сплавов. Так непрерывная регистрация изменений параметров решетки по мере изменения температуры позволяет определить коэффициент теплового расширения. Зависимость параметров элементарной ячейки от наличия примесей в исследуемом веществе позволяет определить состав твердых растворов и фазовые границы на диаграммах равновесия. С помощью точно измеренных размеров элементарной ячейки можно определить плотность, а также молекулярные веса кристаллов. Даже весьма незначительные изменения параметров решетки позволяют выявить причины появления внутренних напряжений в материале, которые часто приводят к дислокационным нарушениям и видимой трещиноватости.

Цель лабораторной работы — определение параметров элементарной ячейки поликристаллических веществ и материалов с помощью рентгеновского структурного анализа.

1. Метод испытаний

1. 1. Рентгеновский структурный анализ

Рентгеновский структурный анализ – методы исследования атомной структуры вещества с использованием явления дифракции рентгеновских лучей. Дифракция рентгеновских лучей возникает при их взаимодействии с электронными оболочками атомов исследуемого вещества. Дифракционная картина зависит от длины волны используемого излучения и атомного строения объекта. Для исследования атомной структуры применяют излучение с длиной волны ≈ 1 Ǻ (≈10 нм), т.е. сопоставимой с размерами атомов.

Кристаллические вещества обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решетку для рентгеновского излучения.

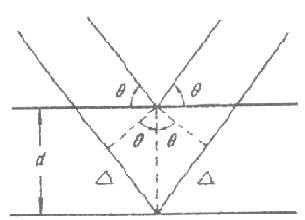
Рис. 2.1.1. К выводу уравнения Вульфа-Брегга

Ход двух пучков рентгеновских лучей через систему из двух атомных плоскостей в кристалле схематично изображен на рис. 2.1.1. Разность хода двух пучков 2Δ. Так как , где d – расстояние между двумя соседними атомными плоскостями (межплоскостное расстояние), то разность хода равна . Для образования конструктивной интерференции (т. е. для отражения пучков в одной фазе) разность хода должна равняться :

(2.1.1)

где d – межплоскостное расстояние, Å ;

– длина волны рентгеновского излучения, Å;

– угол падения (отражения) рентгеновских лучей, град.;

n – порядок отражения (1,2,3, ……)

Соотношение (2.1.1) называется условием Вульфа-Брэгга.

Условие Вульфа-Брэгга позволяет, зная величину и экспериментально измеренные углы , определить значения межплоскостных расстояний изучаемой кристаллической структуры вещества в узлах конструктивной интерференции. Интенсивность этой интерференции связана с симметрией кристаллической решетки. Совокупность значений межплоскостных расстояний с соответствующими значениями зарегистрированной интенсивности интерференции позволяют однозначно идентифицировать анализируемое кристаллическое вещество.

Для определения параметров элементарной ячейки кристаллических материалов необходимо выполнить индицирование атомных плоскостей, т.е. обозначить их индексами, которые определяют их пространственное положение в элементарной ячейке относительно выбранных в ней координатных осей (h, k, l – индексы Миллера).

Индексы Миллера определяют величину расстояния атома l_i, принадлежащего ячейке, от начала координат принятой системы координатных осей в единицах, кратных параметрам ячейки (рис. 2.1.2).

Рис. 2.1.2. Определение межплоскостных расстояний d через индексы Миллера hkl

Межплоскостное расстояние d_hkl по определению равно длине перпендикуляра, опущенного из начала координат на плоскость, пересекающую оси x, у, z. в точках a/h ; .b/k ; c/l.

Параметры элементарной ячейки можно определить, используя формулы для их расчета при различных сингониях кристаллического вещества, т.е. формах его кристаллической ячейки, связывающие эти параметры, межплоскостные расстояниями d_hkl и индексы отражающих плоскостей h, k, 1 (табл. 2.1.1).

Таблица 2.1.I