29)Наибольшее и наименьшее значение функции - определения, иллюстрации.

Кратко остановимся на основных определениях.

Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

30)Выпуклость, вогнутость функции, точка перегиба.

Определение.

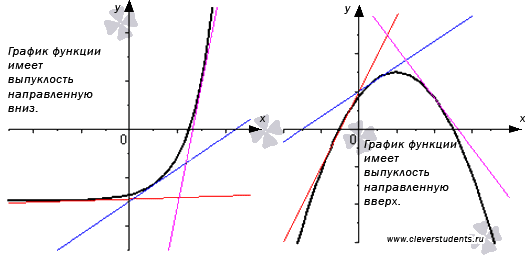
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Определение.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

Точка называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.

Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.

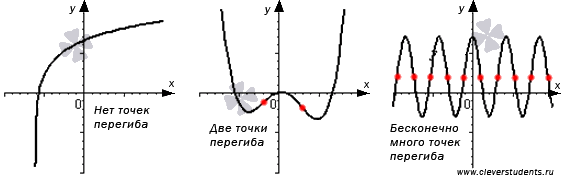
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

азовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

31)Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .

Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

Определение

Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Определение

Прямая называется наклонной асимптотой графика функции , если