21)Производные основных элементарных функций

22)Производная неявной функции

Во многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде. Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом:

• Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

• Решить полученное уравнение относительно производной  y'(x).

Рассмотрим для иллюстрации несколько примеров.

   Пример 1

Продифференцировать функцию y(x), заданную уравнением .

Решение.

Продифференцируем обе части уравнения по переменной x:

     

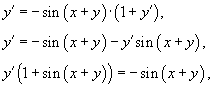
что приводит к результату

     

23)Производные высшего порядка

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

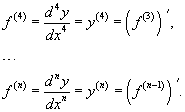
Для нахождения производных высшего порядка можно использовать следующие формулы:

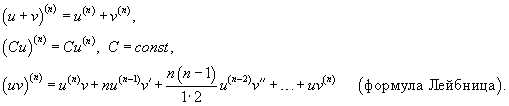
В частности, для производной второго и третьего порядка формула Лейбница принимает вид

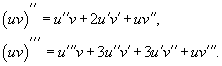
25)Теорема Лагранжа. (О конечных приращениях)

Пусть функция

1. непрерывна на отрезке ;

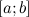2. дифференцируема на интервале .

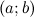Тогда на интервале найдется по крайней мере одна точка , такая, что

26)Правило Лопиталя.

Пусть функции и удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) и в этой окрестности;

3) ;

4) существует конечный или бесконечный.

Тогда существует и , причем

Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.

Замечание

Правило Лопиталя распространяется на случай неопределенности типа при .

27)Возрастание и убывание функции

        функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f (x) ≤ f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х² (рис., а) строго возрастает на отрезке [0,1], а

        

        (рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x)↑, а убывающие f (x)↓. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].

         Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x₀, если найдётся такой интервал (α, β), содержащий точку x₀, что для любой точки х из (α, β), х> x₀, выполняется неравенство f (x₀) ≤ f (x), и для любой точки х из (α, β), х< x₀, выполняется неравенство f (x) ≤ f (x₀). Аналогично определяется строгое возрастание функции в точке x₀. Если f'(x₀) > 0, то функция f (x) строго возрастает в точке x₀. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.

         Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 1, М., 1966.

         С. Б. Стечкин.

        

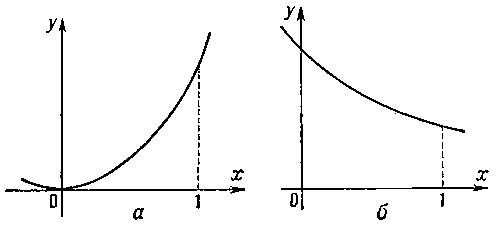
28)Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.