
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой в отрезках на осях
- •Уравнение прямой, проходящей через две различные точки на плоскости
- •6)Бесконечно малая
- •7)Бесконечно большая
- •8)Основные теоремы о пределах
- •9)Признаки существования пределов
- •13)Свойства функций непрерывных в точке
- •21)Производные основных элементарных функций
- •22)Производная неявной функции
- •23)Производные высшего порядка
- •26)Правило Лопиталя.
- •29)Наибольшее и наименьшее значение функции - определения, иллюстрации.
- •30)Выпуклость, вогнутость функции, точка перегиба.
13)Свойства функций непрерывных в точке
1)Если f(x), g(x) – непрерывны в точке x0, то f(x) ± g(x); f(x)•
g(x); f(x)/g(x) (g(x) ≠ 0) – также непрерывны в точке x0.
Докажем, что F(x) = f(x)•g(x) непрерывна в точке x0
Дано: f(x) и g(x) – непрерывны в x0 Û lim f(x) = f(x0); lim g(x) = g(x0)
X ® Xo X ® Xo
lim (f(x)•g(x)) = limf(x)•lim g(x) (по свойству предела функции) = f(x0
)•g(x0) (по
X ® Xo X ® Xo X ® Xo
определению непрерывности) ® F(x) = f(x)•g(x) непрерывна в x0.
![]() 2)
f(x) – непрерывна
2)
f(x) – непрерывна
в точке x0, существует такая окрестность точки
f(x0) > 0 x0
, во всех точках которой f(x) > 0.
Свойства функций, непрерывных на отрезке |
След. » |
Свойство 1: (Первая
теорема Вейерштрасса (Вейерштрасс Карл
(1815-1897) - немецкий математик)). Функция,
непрерывная на отрезке, ограничена на
этом отрезке, т.е. на отрезке
![]() выполняется
условие -
выполняется
условие -
![]() .
.
Доказательство этого
свойства основано на том, что функция,
непрерывная в точке
![]() ,
ограничена в некоторой ее окрестности,
а если разбивать отрезок
на
бесконечное количество отрезков, которые
“стягиваются” к точке
,
то образуется некоторая окрестность
точки
.
,
ограничена в некоторой ее окрестности,
а если разбивать отрезок
на
бесконечное количество отрезков, которые
“стягиваются” к точке
,
то образуется некоторая окрестность
точки
.
Свойство 2: Функция, непрерывная на отрезке , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие
значения
![]() и
и
![]() ,
что
,
что
![]() ,
причем
,
причем
![]() .
.
Отметим эти наибольшие
и наименьшие значения функция может
принимать на отрезке и несколько раз
(например -
![]() ).
).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство
4: Если функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
то существует некоторая окрестность
точки
,
в которой функция сохраняет знак.
,
то существует некоторая окрестность
точки
,
в которой функция сохраняет знак.
Свойство 5: (Первая
теорема Больцано (1781-1848) - Коши). Если
функция
-
непрерывная на отрезке
и
имеет на концах отрезка значения
противоположных знаков, то существует
такая точка внутри этого отрезка, где
![]() .
.
Т.е. если
![]() ,
то
,
то
![]() .
.
Определение. Функция
называется
равномерно непрерывной на отрезке
,
если для любого
![]() существует
существует
![]() такое,
что для любых точек
такое,
что для любых точек
![]() и
и
![]() таких,
что
таких,
что
![]() верно
неравенство
верно
неравенство
![]() .
.
Отличие равномерной
непрерывности от “обычной” в том, что
для любого e существует свое![]() ,
не зависящее от
,
не зависящее от
![]() ,
а при “обычной” непрерывности
зависит
от
,
а при “обычной” непрерывности
зависит
от
![]() и
.
и
.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция
определена,
монотонна и непрерывна на некотором
промежутке, то и обратная ей функция
![]() тоже
однозначна, монотонна и непрерывна.
тоже
однозначна, монотонна и непрерывна.
Пример. Исследовать
на непрерывность функцию и определить
тип точек разрыва, если они есть.
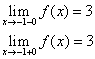
 в
точке
в
точке
![]() функция
непрерывна в точке
функция
непрерывна в точке
![]()
точка разрыва 1 - го рода
14)Задачи,
приводящие к понятию производной
Задача
о скорости. Пусть некоторая
материальная точка совершает неравномерное
движение вдоль прямой. Путь пройденный
телом зависит от времени по закону
![]() .
Зафиксируем некоторый момент времени
.
Зафиксируем некоторый момент времени
![]() ,
за это время был пройден путь
,
за это время был пройден путь
![]() ,
за время
,
за время
![]() будет
пройден путь
.
Тогда за время
будет
пройден путь
.
Тогда за время
![]() тело
пройдет путь
тело
пройдет путь
![]() .
Отношение
.
Отношение
![]() –
средняя скорость за промежуток времени
.
Будем стремить
–
средняя скорость за промежуток времени
.
Будем стремить
![]() к
нулю. В таком случае говорят о предельной
скорости и
к
нулю. В таком случае говорят о предельной
скорости и
![]() называют
мгновенной скоростью тела в момент
времени
.
Задача о касательной.
Рассмотрим другую задачу, связанную с
построением касательной к кривой. На
некоторой кривой зафиксируем точку
называют
мгновенной скоростью тела в момент
времени
.
Задача о касательной.
Рассмотрим другую задачу, связанную с
построением касательной к кривой. На
некоторой кривой зафиксируем точку
![]() .
Возьмем некоторую произвольную точку
.
Возьмем некоторую произвольную точку
![]() и
будем стремить ее по кривой в точке
.
Проведем секущую
.
При движении
к
секущая
будет поворачиваться вокруг точки
и
займет свое предельное положение, когда
и
будем стремить ее по кривой в точке
.
Проведем секущую
.
При движении
к
секущая
будет поворачиваться вокруг точки
и
займет свое предельное положение, когда
![]() .
Определение 1. Касательной
к данной кривой в данной точке называется
предельное положение секущей
при
стремлении точки
к
точке
.
Рассмотрим случай, когда
кривая задана функцией
.
Определение 1. Касательной
к данной кривой в данной точке называется
предельное положение секущей
при
стремлении точки
к
точке
.
Рассмотрим случай, когда
кривая задана функцией
![]() .
(Рис. 29)
Придадим аргументу
.
(Рис. 29)
Придадим аргументу
![]() приращение
приращение
![]() ,
тогда приращение функции составит
,
тогда приращение функции составит
![]() .
Очевидно, что когда
.
Очевидно, что когда
![]() ,
угол
,
угол
![]() стремится
к углу
стремится
к углу
![]() .
.
![]() ,
тогда при
,
тогда при
![]() получаем,
что
получаем,
что
![]() .
.
15)Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Связь между дифференцируемостью и непрерывностью функции |
Теорема. Если функция
Доказательство.
Пусть функция
Дифференцируема
в точке X. Это значит, что ее
производная
Существует и конечен. По определению предела это значит, что
То есть при малых
Обратно, если функция непрерывна в некоторой точке X, то это еще не значит, что она дифференцируема в этой точке. Например, функция , график которой изображен на рис. 4.7, непрерывна в любой точке X, ибо её график сплошной (без разрывов). И тем не менее в точках X1, X2 и X3, как было показано выше, она не дифференцируема. |
16)Вычисление
производной функции у = f(x)
производится по следующей схеме:
1)
Находим приращение функции на отрезке
![]() :
:
![]() 2)
Делим приращение функции на приращение
аргумента:
2)
Делим приращение функции на приращение
аргумента:
![]() 3)
Находим предел
3)
Находим предел
![]() устремляя
устремляя
![]() к нулю. Переход к пределу мы будем
записывать с помощью знака lim:
к нулю. Переход к пределу мы будем
записывать с помощью знака lim:
![]()
Пусть функции
![]() и
и
![]() имеют
производные в точке
имеют
производные в точке
![]() .
Тогда
.
Тогда
1. Константу можно выносить за знак производной.
![]()
Пример
![]()
Больше примеров решений →
2. Производная суммы/разности.
Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
![]()
Пример
![]()
Больше примеров решений →
3. Производная произведения.
![]()
Пример
![]()
Больше примеров решений →
4. Производная частного.
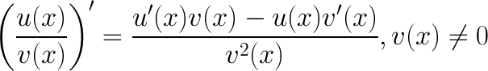
Пример
![]()
Больше примеров решений →
5. Производная сложной функции.
Производная сложной
функции равна производной этой функции
по промежуточному аргументу
![]() ,
умноженной на производную от промежуточного
аргумента
по
основному аргументу
.
,
умноженной на производную от промежуточного
аргумента
по
основному аргументу
.
![]() и
и
![]() имеют
производные соответственно в точках
имеют
производные соответственно в точках
![]() и
и
![]() .
Тогда
.
Тогда
![]()
Теорема
(О производной обратной функции)
Если функция
![]() непрерывна
и строго монотонна в некоторой окрестности
точки
и
дифференцируема в этой точке, то обратная
функция
непрерывна
и строго монотонна в некоторой окрестности
точки
и
дифференцируема в этой точке, то обратная
функция
![]() имеет
производную в точке
имеет
производную в точке
![]() ,
причем
,
причем
![]() .
.


 при
при
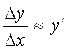 ,
откуда
,
откуда