1)Матрицей размера m x n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,…. Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: a_ij, где i - номер строки, j - номер столбца. Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij = b_ij для любых i=1,2,…m; j=1,2,…n, виды матриц. Матрица, состоящая из одной строки, называется матрицей (вектором)- строкой, а из одного столбца - матрицей (вектором)- столбцом: Элементы матрицы a_ij, у которых номер столбца равен номеру строки называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a₁₁, a₂₂,…,a_nn. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. 2)«Операции над матрицами Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые - специфические. 1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B= A, элементы которой b_ij= a_ij для i=1,2,…m; j=1,2,…n Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы. В частности, произведение матрицы А на число 0 есть нулевая матрица. 2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_ij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно). 3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B. 4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m ∙B _k называется такая матрица C_m , каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: 5.Возведение в степень. Целой положительной степенью (mквадратной матрицы А называется произведение m матриц, равных А, т.е. 6.Транспонирование матрицы- переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А. 3)Определителем (детерминантом) – го порядка или определителем (детерминантом) квадратной матрицы – го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками. Определитель второго порядка Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: Примеры определителей второго порядка: Определитель третьего порядка. Определителем третьего порядка называется следующее выражение: Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. Примеры определителей третьего порядка:

4)Сначала опишем основные свойства определителей относительно преобразования матриц. Знание этих свойств поможет упрошать вычисления и находить определители произвольного порядка. Свойство 1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами). Исходя из первого свойства, в остальных свойствах мы можем говорить только о строках, подразумевая, что эти свойства применимы также и к столбцам. Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю. Свойство 3. От перестановки двух строк определитель меняет свой знак. Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю. Свойство 5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число. Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю. Свойство 7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: a_ij=b_j+c_j, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j. Свойство 8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю.. Свойство 9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк. Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы nЧn равен (алгебраическое дополнение A_ij=(-1)^i+jM_ij. Здесь минор M_ij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца) Теорема о разложении определителя по строке позволяет свести вычисление определителя матрицы nЧn к вычислению n определителей матриц (n-1)Ч(n-1). Таким образом, вычисление определителей с порядком выше третьего сводится к разложению на сумму определителей третьего порядка. С помощью описанных выше свойств определителей можно провести предварительные преобразования матрицы, облегчающие дальнейшие вычисления. Например, если перед разложением определителя n-го порядка по какой-либо строке накопить в этой строке нули, то разложение приводит к меньшему количеству определителей порядка n-1. Ниже приводится пример, в котором сначала из первой строки вычитается вторая (при этом появляются два нуля), а затем идет разложение по первой строке (из-за двух нулей получается не четыре определителя третьего порядка, а только два): 3.Теорема Лапласа. Миноры и Алгеб.дополнения.Пусть  A  – квадратная матрица  n-го порядка.       Определитель  k-го порядка, составленный из элементов матрицы  A, расположенных на пересечении строк с номерами  i₁ ,  i₂ , ...,  i_k  и столбцов с номерами  j₁ ,  j₂ , ...,  j_k , называется минором  M   k-го порядка матрицы  A. Если из матрицы  A  вычеркнуть строки и столбцы с такими номерами, то определитель  n–k-го порядка полученной матрицы называется дополнительным минором для минора  M.      Обозначим символом  S  сумму индексов, нумерующих строки и столбцы такого минора: S= i₁ + j₁ + i₂ + j₂ + ... + i_k + j_k . Алгебраическим дополнением минора  M  называется дополнительный минор для минора  M, умноженный на  (–1)^S.       Отметим, что алгебраическое дополнение  A_i j  элемента  a_i j  (минора первого порядка) является частным случаем алгебраического дополнения минора. Теорема Лапласа. Пусть  D  – определитель  n-го порядка, в котором произвольно выбраны  k  строк (или столбцов), где  1 ?k ? n – 1. Тогда определитель  D  равен сумме произведений всех миноров  k-го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения. 5) Понятие обратной матрицы вводится только для квадратных матриц. Матрица называется обратной матрицей для квадратной матрицы , если .       Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию . Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Из определения обратной матрицы следует, что матрица является обратной для матрицы , то есть . Про матрицы и можно говорить, что они обратные друг другу или взаимно обратны. Итак, чтобы найти обратную матрицу нужно: 1.Найти определитель матрицы A. 2.Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу , элементами которой являются числа Aij. 3.Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет Свойства обратной матрицы

• , где det обозначает определитель.

• для любых двух обратимых матриц A и B.

• где * обозначает транспонированную матрицу.

• для любого коэффициента .

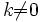Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если существует, то x = b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. 6)Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Обычно ранг матрицы A обозначается ( ) или . 2 метода вычисления ранга матрицы: 1) метод окаймляющих миноров; 2) метод элементарных преобразований. Суть первого метода заключается в следующем. Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется. Что касается второго метода, то воспользуемся элементарными преобразованиями 1) перестановка двух любых строк (или столбцов),2) умножение строки (или столбца) на отличное от нуля число,3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число. 7 и 8) Система n линейных уравнений с n неизвестными. Правило Крамера. Пустьдана система n  линейных уравнений с  n неизвестными. или в матричной форме А*Х=В. Основная матрица А такой  системы  квадратная. Определитель этой матрицы называется определителем  системы. Если определитель  системы  отличен от нуля, то система  называется невырожденной. Найдем решение данной  системы   уравнений  в случае   Умножив обе части  уравнения  А*Х=В слева на матрицу A^-1, получим A^-1*A*X=A^-1*B Поскольку. A^-1*A=E  и Е*Х=Х , то X=A^-1*B        (4.1) Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов Отыскание решения  системы  по формуле (4.1) называют матричным способом решения системы . Матричное равенство (4.1) запишем в виде  то есть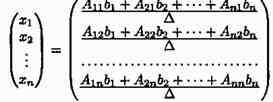 Отсюда следует, что Но   есть разложение определителя по элементам первого столбца. Определитель получается из определителя    путем замены первого столбца коэффициентов столбцом из свободных членов. Итак, Аналогично:  , где  2  получен из    путем замены второго столбца коэффициентов столбцом из свободных членов: ,..., Формулы называются формулами Крамера.Итак, невырожденная  система   n   линейных   уравнений   с   n   неизвестными  имеет единственное решение, которое может быть найдено матричным способом, либо по формулам Крамера Правило Крамера.Если в системе   линейных уравнений с   неизвестными   , то система имеет решение и притом единственное. Это решение задается формулами Доказательство.     По теореме 14.1 обратная матрица находится по формуле где   -- алгебраические дополнения. Тогда из (15.3) следует, что Заметим, что по формуле (14.13) разложение определителя   по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя   по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому   , откуда и следует утверждение теоремы.       Решение системы n линейных уравнений с n неизвестными методом обратных матриц. Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением. Пусть определитель матрицы отличен от нуля |A| ? 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу, обратную матрице A: . Поскольку A = E и E∙X = X, то получаем решение матричного уравнения в виде X = B. Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = B.Для того чтобы решить  систему   линейных   уравнений   методом   обратной   матрицы, необходимо выполнить следующие действия:

• сформировать  матрицу  коэффициентов и вектор свободных членов заданной  системы ;

• решить  систему , представив вектор  неизвестных  как произведение  матрицы ,  обратной  к  матрице  системы , и вектора свободных членов

Пример: Дана  система   уравнений : Решаем : A=; b=[2; -1; -2]; x=inv(A)*b %  Решение   системы  x=A^-1b Результатом будет: x = 0.5200 0.0800 1.6400 9 и 10)Система m линейных уравнений с n неизвестными. Метод Гаусса. Система m линейных уравнений с n неизвестными (или, линейная система) в  линейной  алгебре — это  система   уравнений  вида

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты  системы  — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij)  системы  обозначают номера  уравнения  (i) и  неизвестного  (j), при котором стоит этот коэффициент, соответственно^[1].  Система  (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.  Система  (1) называется квадратной, если число  m   уравнений  равно числу  n   неизвестных . Решение  системы  (1) — совокупность  n  чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в  систему  (1) обращает все её  уравнения  в тождества.  Система  (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Совместная система вида (1) может иметь одно или более решений. Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной  системы  вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная  система  вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если  уравнений  больше, чем  неизвестных , она называется переопределённой. Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Таким образом, процесс решения системы линейных алгебраических уравнений по методу Гаусса состоит из двух этапов. Первый этап (прямой ход метода) – система приводится к треугольному виду.Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Пример 2.13. Решить систему уравнений методом Гаусса: x +  y - 3z = 2, 3x - 2y +  z = - 1, 2x +  y - 2z = 0. Решение. Выпишем расширенную матрицу данной системы и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:  ~  ; б) третью строку умножим на (-5) и прибавим к ней вторую: . В результате всех этих преобразований данная система приводится к треугольному виду:                                                     x + y - 3z = 2,                                                     -5y + 10z = -7,                                                            - 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = - 0,7. 11)Система линейных однородных уравнений. Пусть дана система линейных однородных уравнений Очевидно, что однородная система всегда совместна , она имеет нулевое (тривиальное) решение x1=x2=x3=...=xn=0. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r Необходимость: Так как ранг не может превосходить размера матрицы, то, очевидно, rn. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n. Достаточность: Пусть r Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель D был равен нулю, т. е. D=0. Если система имеет ненулевые решения, то D=0. Ибо при D№0 система имеет только единственное, нулевое решение. Если же D=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r</n.

12 и 13)Векторы на плоскости и в пространстве

Данный раздел рассматривает универсальный метод решения задач типа С.Вектор  — это направленный отрезок. Его длиной считают длину отрезка.Если даны две точки M₁ (x₁, y₁, z₁) и M₂ (x₂, y₂, z₂), то вектор Расстояние между двумя точками — это длина отрезка М₁М₂ или длина вектора n: Если даны два вектора и , то:

1. Длины векторов:

2. Сумма векторов: Суммой двух векторов a и b является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма ); или вектор, соединяющий начало первого вектора с концом последнего — по правилу треугольника.Суммой трех векторов a, b, c называется диагональ параллелепипеда, построенного на этих векторах(правило параллелепипеда ).

3. Разность векторов:

4. Умножение вектора на число (скаляр): Векторы t и b называются коллинеарными , т.е. лежат на параллельных прямых или на одной прямой. Пропорциональные координаты — условие коллинеарности векторов.

5. Скалярное произведение векторов: Если скалярное произведение равно нулю, то векторы перпендикулярны.

6. Угол между векторами a и b, точнее его косинус:

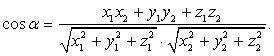
7. Векторное произведение векторов: где S — площадь параллелограмма, построенного на векторах a, b.Если , то данные векторы коллинеарные (параллельны прямой).

8. Смешанное произведение векторов 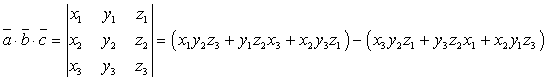Если , то данные векторы компланарные (принадлежат плоскости или параллельны ей).Три ненулевых вектора a, b, cкомпланарны, когда один из них выражается через два других, т.е. , где n, m — числа.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. .

Векторы на плоскости и в пространстве - основные определения.

В этой статье мы дадим определение вектора с точки зрения геометрии, а также основные сопутствующие понятия. На плоскости и в пространстве вектор является полноценным геометрическим объектом, то есть, имеет вполне реальные очертания, которые Вы увидите на приведенных графических иллюстрациях.

Определение.

Вектор – это направленный отрезок прямой.

То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.

Для обозначения векторов будем использовать строчные латинские буквы со стрелочкой над ними, например . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как .

Определение.

Нулевой вектор – это любая точка плоскости или пространства.

Будем считать, что нулевому вектору можно придать любое направление на плоскости и в пространстве.

Определение.

Длина вектора - это неотрицательное число, равное длине отрезка АВ.

Длину вектора будем обозначать как .

Так как обозначение длины вектора в точности совпадает со знаком модуля, то можно услышать, что длину вектора называют модулем вектора. Все же рекомендуем использовать термин "длина вектора". Длина нулевого вектора равна нулю.

Определение.

Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Определение.

Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.

Нулевой вектор коллинеарен любому другому вектору.

Определение.

Два коллинеарных вектора и называют сонаправленными, если их направления совпадают и обозначают .

Определение.

Два коллинеарных вектора и называют противоположно направленными, если их направления противоположны и обозначают .

Будем считать, что нулевой вектор сонаправлен с любым другим вектором.

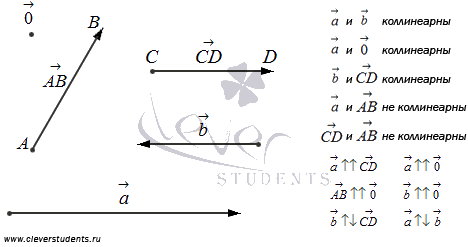
Определение.

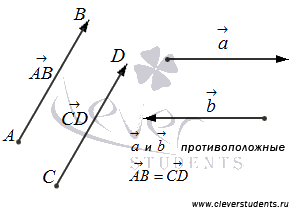
Два вектора называются равными, если они сонаправленные и их длины равны.

Определение.

Два вектора называются противоположными, если они противоположно направлены и их длины равны.

Понятие равных векторов дает нам возможность рассматривать векторы без привязки к конкретным точкам. Другими словами, мы имеем возможность заменить вектор равным ему вектором, отложенным от любой точки.

Пусть и два произвольных вектора на плоскости или в пространстве. Отложим от некоторой точки O плоскости или пространства векторы и . Лучи OA и OB образуют угол .

Определение.

Угол называется углом между векторами и .

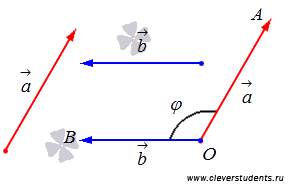
Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами равен 180 градусам (или радиан).

Определение.

Два вектора называются перпендикулярными, если угол между ними равен 90 градусам (или радиан).

20)Уравнение линии на плоскости — это уравнение, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Если точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами. Чтобы убедится, лежит ли точка на данной линии, надо проверить, удовлетворяют ли координаты этой точки уравнению. Уравнения линии могут быть самыми различными, но не каждое уравнение имеет геометрический образ в виде линии.

Примеры:

1. Уравнение окружности: (x — x_о)² + (y — y_о)² = r²

2. Уравнение прямой с угловым коэффициентом: y = k·x + b

21)Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x

+

B y

+

C

= 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y

=

k x

+

b

где

k

- угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (

a

, 0) и (0,

b

), то она может быть найдена используя формулу уравнения прямой в отрезках

x	+	y	= 1
a		b

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(

x

₁,

y

₁) и B(

x

₂,

y

₂), такие что

x

₁ ≠

x

₂ и

y

₁ ≠

y

₂ то уравнение прямой можно найти, используя следующую формулу

x - x 1	=	y - y 1
x 2 - x 1		y 2 - y 1

22). Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

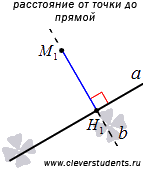
Расстояние от точки до прямой – определение.

Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.

Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M₁, не лежащая на прямой a. Проведем через точку M₁ прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H₁. Отрезок M₁H₁ называется перпендикуляром, проведенным из точки M₁ к прямой a.

Определение.

Расстоянием от точки M₁ до прямой a называют расстояние между точками M₁ и H₁.

Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.

Определение.

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.

Это определение эквивалентно первому определению расстояния от точки до прямой.

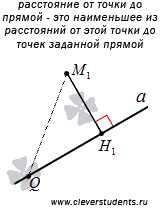
Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.

Возьмем на прямой a точку Q, не совпадающую с точкой M₁. Отрезок M₁Q называют наклонной, проведенной из точки M₁ к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M₁ к прямой a, меньше любой наклонной, проведенной из точки M₁ к прямой a. Это действительно так: треугольник M₁QH₁ прямоугольный с гипотенузой M₁Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .

К началу страницы

Расстояние от точки до прямой на плоскости – теория, примеры, решения.

В зависимости от исходных данных для нахождения расстояния от точки до прямой можно использовать различные методы геометрии: теорему Пифагора, определения синуса, косинуса, тангенса угла, признаки равенства и подобия треугольников и т.п. Множество подобных задач решается на уроках геометрии в средней школе.

Если же при нахождении расстояния от точки до прямой есть возможность ввести прямоугольную систему координат, то можно воспользоваться методом координат. В этом пункте статьи мы подробно остановимся на двух способах нахождения расстояния от точки M₁ до прямой a, которые заданы в прямоугольной декартовой системе координат Oxy на плоскости. В первом случае расстояние от точки M₁ до прямой a мы будем искать как расстояние от точки M₁ до точки H₁, где H₁ – основание перпендикуляра, опущенного из точки M₁ на прямую a. Во втором способе нахождения расстояния от точки M₁ до прямой a будем использовать нормальное уравнение прямой a.

Итак, поставим перед собой следующую задачу: пусть на плоскости зафиксирована прямоугольная система координат Oxy, задана точка , прямая a и требуется найти расстояние от точки M₁ до прямой a. Разберем по-очереди два способа ее решения.

Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.

Если мы определим координаты точки H₁, то искомое расстояние мы сможем вычислить, используя формулу для нахождения расстояния от точки M₁ до точки H₁ по их координатам: .

Осталось разобраться с нахождением координат точки H₁.

Мы знаем, что прямой линии в прямоугольной системе координат Oxy соответствует некоторое уравнение прямой на плоскости. Будем считать, что способ задания прямой a в условии задачи позволяет написать общее уравнение прямой a или уравнение прямой с угловым коэффициентом. После этого мы можем составить уравнение прямой, проходящей через заданную точку M₁ перпендикулярно заданной прямой a. Обозначим эту прямую буквой b. Тогда точка H₁ – это точка пересечения прямых a и b, следовательно, координаты точки H₁ можно определить, обратившись к материалу статьи координаты точки пересечения двух прямых.

Итак, мы получили алгоритм для нахождения расстояния от заданной точки до заданной прямой a:

• находим общее уравнение прямой a вида 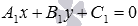или уравнение прямой a с угловым коэффициентом ;

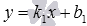• получаем общее уравнение прямой b вида 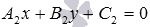или уравнение прямой b с угловым коэффициентом вида 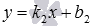, учитывая, что прямая b проходит через заданную точку M₁ и перпендикулярна заданной прямой a;

• определяем координаты точки H₁ - точки пересечения прямых a и b, решая систему линейных уравнени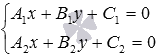й или ;

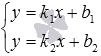• вычисляем требуемое расстояние от точки M₁ до прямой a по формуле .

Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.

Следующая теорема отвечает на вопрос: «Как найти расстояние от заданной точки до заданной прямой на плоскости»?

Теорема.

В прямоугольной системе координат Oxy на плоскости расстояние от точки до прямой a, заданной нормальным уравнением прямой вида , равно модулю значения выражения, находящегося в левой части нормального уравнения прямой, вычисленного при , то есть, .

Доказательство.

Так как прямой a в прямоугольной системе координат Oxy на плоскости соответствует нормальное уравнение прямой , то - нормальный вектор прямой a единичной длины, а расстояние от начала координат до прямой a равно p единиц. Изобразим эти данные на чертеже, а также добавим точку , радиус-вектор точки М₁ - , построим искомое расстояние от точки М₁ до прямой a - , покажем проекции М₂ и H₂ точек М₁ и H₁ соответственно на прямую, проходящую через точку O и имеющую направляющий вектор , обозначим числовую проекцию вектора на направление вектора как .

В зависимости от расположения точки М₁ относительно прямой a возможны следующие варианты.

Все полученные результаты можно описать одной формулой: . Осталось привести полученное равенство к виду , то есть показать, что .

Определение скалярного произведения векторов дает нам равенство 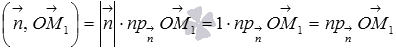, а это же самое скалярное произведение в координатной форме имеет вид , следовательно, . Тогда , что и требовалось доказать.

Таким образом, чтобы найти расстояние от точки до прямой a на плоскости нужно:

• получить нормальное уравнение прямой a в виде (если оно сразу не дано);

• вычислить значение выражения 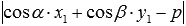- полученное значение является искомым расстоянием .

23)Окружность — геометрическое место точек плоскости, удалённых от некоторой точки — центра окружности — на заданное расстояние, называемое радиусом окружности.

Общее уравнение окружности записывается как:

или

где

24)Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F_1 и F_2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

|F_1M|+|F_2M|=2a, причем |F_1F_2|<2a.

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

25)Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее,

причем

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.

26)Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

2)Функция- зависимость переменной у от переменной x, если

каждому значению х соответствует единственное значение у.

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.

3)Элементарные функции, класс функций, состоящий из многочленов, рациональных функций, показательных функций, логарифмических функций, тригонометрических функций и обратных тригонометрических функций, а также функций, получающихся из перечисленных выше с помощью четырёх арифметических действий и суперпозиций (образование сложной функции), примененных конечное число раз; например,

,

y = x^a = e^{a ln x};

Алгебраические функции.

Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня.

Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты.

Например, функция 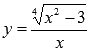является алгебраической.

Алгебраические функции подразделяются на рациональные и иррациональные.

Рациональные функции.

Рациональными называются алгебраические функции, которые не содержат аргумент под знаком радикала (корня).

Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов).

Пример целой рациональной функции: .

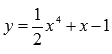Пример дробно-рациональной функции: .

ПРИМЕЧАНИЕ:

Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, 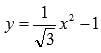- целая рациональная функция, а не иррациональная.

Иррациональные функции.

Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня).

Примером может являться функция .

К началу страницы

Трансцендентные функции.

Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций).

К примеру, 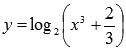- трансцендентная функция.

К началу страницы

ОБРАТИТЕ ВНИМАНИЕ!

Если вид элементарной функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция.

К примеру, - не иррациональная функция, а рациональная, так как .

- не трансцендентная функция, а рациональная алгебраическая, так как .

Преобразования графиков функций — это линейные преобразования функции y = f(x) или её аргумента x к виду y = af(kx + b) + m, а также преобразование с использованием модуля.

Зная, как строить графики функции y = f(x), где y = kx + b, y = ax², y = xⁿ , y=xk, y = sin x, y = cosx, y = tgx, y = ctgx, y=ax y=logax , можно построить график функции y = af(kx + b) + m.

Общий вид функции	Преобразования
y = f(x - b)	Параллельный перенос графика вдоль оси абсцисс на | b | единиц вправо, если b > 0; влево, если b < 0.
y = f(x + b)	влево, если b > 0; вправо, если b < 0.
y = f(x) + m	Параллельный перенос графика вдоль оси ординат на | m | единиц вверх, если m > 0, вниз, если m < 0.
	Отражение графика
y = f( - x)	Симметричное отражение графика относительно оси ординат.
y = - f(x)	Симметричное отражение графика относительно оси абсцисс.
	Сжатие и растяжение графика
y = f(kx)	При k > 1 — сжатие графика к оси ординат в k раз, при 0 < k < 1 — растяжение графика от оси ординат в k раз.
y = kf(x)	При k > 1 — растяжение графика от оси абсцисс в k раз, при 0 < k < 1 — cжатие графика к оси абсцисс в k раз.
	Преобразования графика с модулем
y = | f(x) |	При f(x) > 0 — график остаётся без изменений, при f(x) < 0 — график симметрично отражается относительно оси абсцисс.
y = f( | x | )	При x 0 — график остаётся без изменений, при x < 0 — график симметрично отражается относительно оси ординат.

4)Число называется пределом числовой последовательности , если последовательность является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

5)Пусть функция f(x) определена в некоторой проколотой окрестности точки x0 .

Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε,   т.е.

lim

x → x0

f(x) = A     ЬЮ     " ε > 0   $ δ > 0 :     0 < |x − x0| < δ Ю |f(x) − A| < ε.

Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.