Ещё пример задания:

Дано: 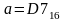и 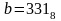. Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет неравенству a < c < b?

1) 11011001₂ 2) 11011100₂ 3) 11010111₂ 4) 11011000₂

Общий подход:

перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить.

Решение (вариант 4, через шестнадцатеричную систему):

1. никуда переводить не нужно;

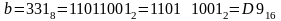2. (сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F);

3. переводим в шестнадцатеричную систему все ответы:

11011001₂ = 1101 1001₂ = D9₁₆ (разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F, как в п. 1)

11011100 ₂= DC₁₆, 11010111₂ = D7₁₆, 11011000₂=D8₁₆

4. в шестнадцатеричной системе между числами D7₁₆ и D9₁₆ может быть только D8₁₆

5. таким образом, верный ответ – 4 .

Выводы:

• есть несколько способов решения, «каждый выбирает для себя»;

• наиболее сложные вычисления – при переводе всех чисел в десятичную систему, можно легко ошибиться;

• сравнивать числа в двоичной системе сложно, также легко ошибиться;

• видимо, в этой задаче наиболее простой вариант – использовать восьмеричную систему, нужно просто запомнить двоичные записи чисел от 0 до 7 и аккуратно все сделать;

• в других задачах может быть так, что выгоднее переводить все в десятичную или шестнадцатеричную систему счисления.

A2 (базовый уровень, время – 2 мин)

Тема: Использование информационных моделей (таблицы, диаграммы, графики). Перебор вариантов, выбор лучшего по какому-то признаку.

Что нужно знать:

• в принципе, особых дополнительных знаний, кроме здравого смысла и умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется

• полезно знать, что такое граф (это набор вершин и соединяющих их ребер) и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания

• чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки

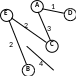
• рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 4 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 4; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет

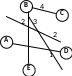
	A	B	C	D	Е
A			3	1
B			4		2
C	3	4			2
D	1
Е		2	2

• обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее

• в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)

• желательно научиться быстро (и правильно) строить граф по весовой матрице и наоборот