32) Двумерная случайная величина, функция распределения и ее свойства.

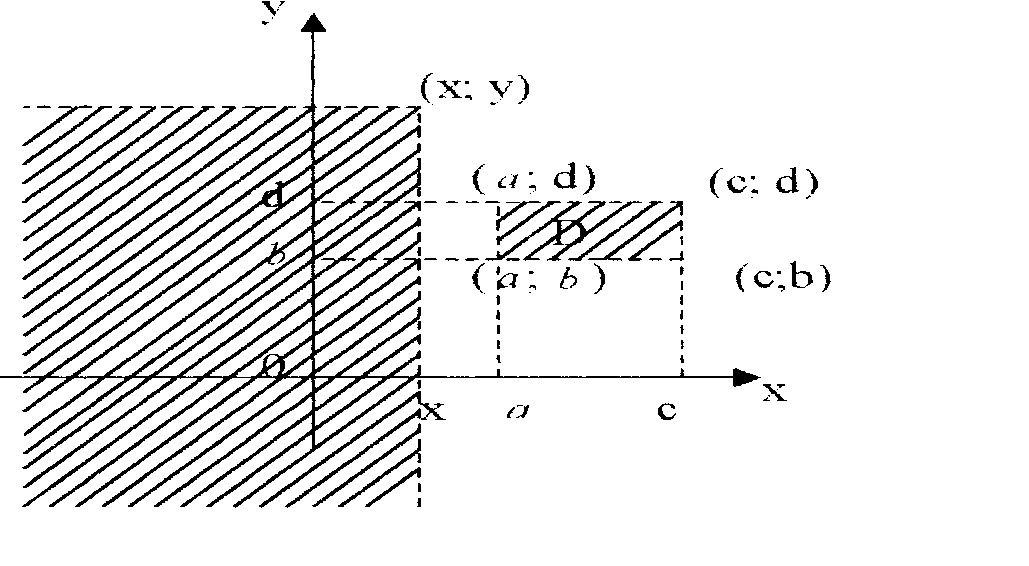
Функцией распределения F(x,y) случайной величины (ξ;η) назовем F(x,y)=P(ξ<x,η<y), т.е. F(x,y) - вероятность попадания точки (ξ; η) в левый нижний бесконечный квадрат плоскости Оху с вершиной в точке (х;у).

Свойства Функции распределения F(x,y):

• 0 < F(x,y) £ 1.

• F(x,-¥)=F(-¥,y)=F(-¥,+¥)=0.

• F(+¥ ,+¥) =1.

• F(x; ,+¥)=F₁(x).

• F(+¥,y) =F₂(y).

• F(x,y) - функция неубывающая по каждому аргументу

• Для прямоугольной области

P((ξ;η)ÎD)=F(c;d)-F(a;d)-F(c;b)+F(a;b).

32. Функция случайного аргумента. Закон распределения для дискретной случайной величины, вывод формулы для плотности непрерывной случайной величины.

Функции случайных аргументов

Функция η=g(ξ) называется функцией случайного аргумента ξ, если каждому возможному значению случайной величины ξ ставится в соответствие по правилу g одно из возможных значений случайной величины η.

Закон распределения функции случайных аргументов

1.ξ- дискретная случайная величина, т.е. ее ряд распределения имеет вид

ξ х₁ х₂ ... х_n

Р р₁ р₂ ... р_n

• Если различным возможным значениям случайной величины ξ соответствуют различные возможные значения случайной величины η, то вероятности соответствующих значений случайных величин ξ и η равны, т.е. если

Р(ξ=х_i) = p_i, то и P(η= g (x_i)) = p_i.

Пример: η=ξ²

• Если различным возможным значениям случайной величины ξ соответствуют значения η, среди которых есть равные между собой, то вероятности повторяющихся значений случайной величины η равны суммам вероятностей соответствующих значений случайной величины ξ.

• Пример: η=ξ²

• 

Решение.

Т.к. P(η=1)=P(ξ=1)=0,3;

P (η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то

ξ - непрерывная случайная величина, т.е. известна плотность распределения случайной величины f_ξ(x). Пусть функция y=g(x) - непрерывна, монотонна и дифференцируема на всем интервале возможных значений случайной величины ξ. Тогда существует обратная функция х = g^-1(у), также непрерывная, монотонная и дифференцируемая. Тогда плотность вероятности случайной величины η=g(ξ) равна

f_η(x) = f_ξ(g^-1(у))×|[g^-1(у)]^/|.

З амечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f _{η i}(y) для каждого интервала, а затем

Ч исловые характеристики функций случайного аргумента

34. Числовые характеристики двумерной случайной величины: моменты, ковариация, коэффициент корреляции. Свойства (теоремы) для математического ожидания и дисперсии.

Числовые характеристики двумерной случайной величины

Начальным моментом порядка k+s случайной величины (ξ,η) называется

Согласно определению математического ожидания

Центральным моментом порядка k+s случайной величины (ξ,η) называется

Например,

₁₀=M[ξ¹ η⁰]=m_ξ, ₀₁=M[ξ⁰ η¹]=m_η,

₁₀=M[ξ – m_ξ]=0, ₀₁=M[η – m_η]=0,

₂₀=M[(ξ – m_ξ)²]=D_ξ,  ₀₂=M[(η – m_η)²]=D_η,

₁₁=M[(ξ – m_ξ)(η – m_η)]=k_ξη называется моментом корреляции (иначе моментом связи) или ковариацией случайных величин ξ и η.

Для ковариации справедлива формула:

k_ξη =M[(ξ – m_ξ)(η – m_η)]=M[ξη] – m_ξ m_η.

Коэффициентом корреляции назовем

Случайные величины ξ и η, для которых k_ξη = 0 (а значит и r_ξη =0), называются некоррелированными (несвязанными).

Если k_ξη  0 (а значит и r_ξη 0), то ξ и η называются коррелированными (это есть признак наличия зависимости между ними).

Можно доказать, что если ξ и η независимые случайные величины, то k_ξη =0 (а значит и r_ξη =0),

т.е. ξ и η некоррелированные величины

Заметим, что из некоррелированности случайных величин, в общем случае, еще не следует их независимость. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми.

Итак:

• из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность.

• Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

• Числа k_ξη и r_ξη характеризуют не всякую зависимость, а только так называемую линейную зависимость между случайными величинами ξ и η. Некоррелированность эквивалентна линейной независимости.

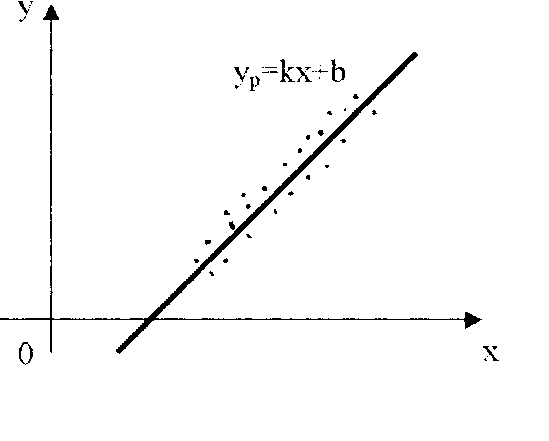
Найдем линейную зависимость у=kx+b , которая давала бы возможность предсказывать как можно точнее значения случайной величины η по значениям случайной величины ξ, т.е. такую линейную зависимость, чтобы ошибка предсказания M[(η-y)²], была минимальной.

В этом случае

Таким образом, уравнение искомой прямой имеет вид

и называется прямой среднеквадратической регрессии η на ξ

- коэффициент регрессии η на ξ.

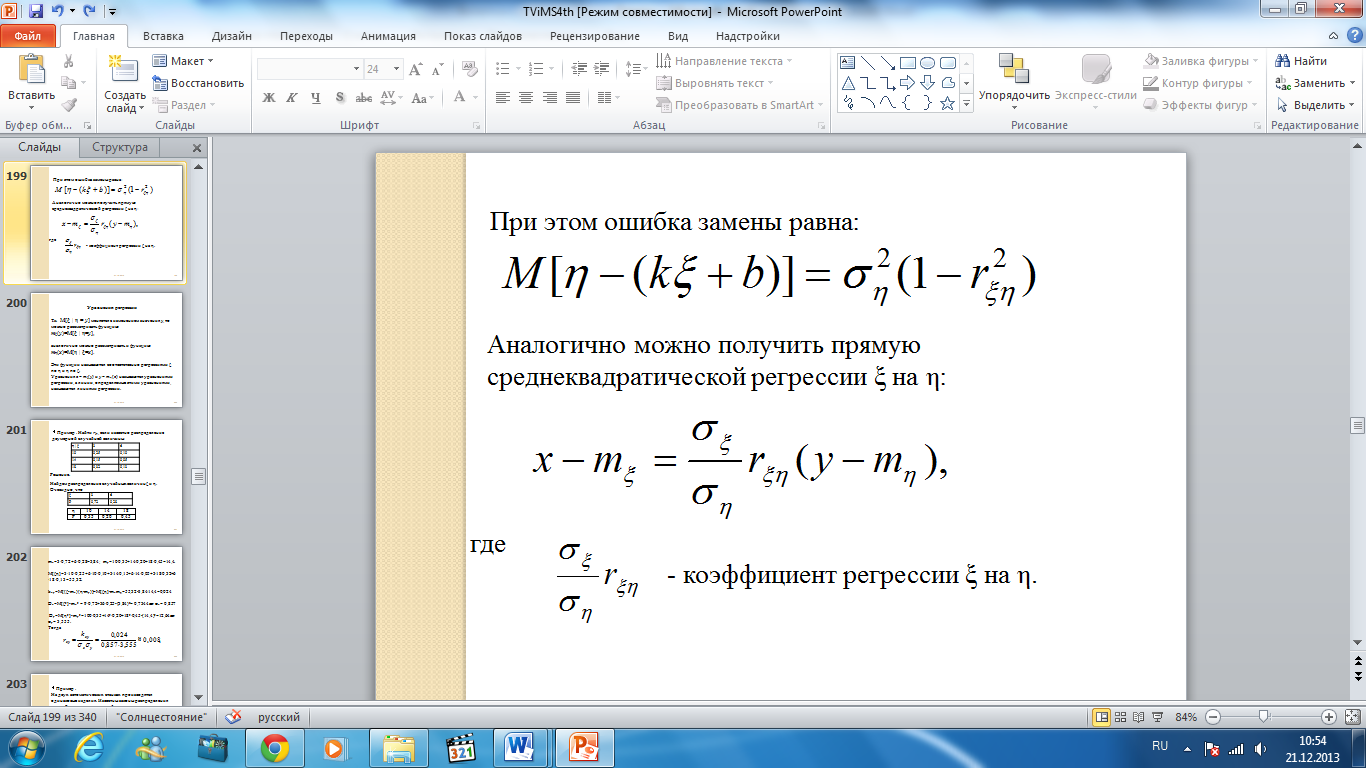
При этом ошибка замены равна:

Аналогично можно получить прямую среднеквадратической регрессии ξ на η:

- коэффициент регрессии ξ на η.

1. Основные теоремы о математических ожиданиях и дисперсиях

Теорема. M[ξη]= m_ξ m_η + k_ξη

Следствие. Если ξ и η независимые случайные величины, то M[ξη]= m_ξ m_η

Теорема. D[ξ+η]=D[ξ]+D[η] + 2k_ξη

Следствие. Если ξ и η - независимые случайные величины, то D[ξ+η]=D[ξ]+D[η].