30. Нормальное непрерывное распределение, функция распределения и плотность, математическое ожидание и дисперсия, вероятность попадания в интервал, правило трех сигм.

Нормальное распределение

Непрерывная случайная величина ξ имеет нормальное распределение, если плотность вероятности

Нормальное распределение с параметрами a =0 и =1 называется стандартным (основным), плотность вероятности в этом случае обозначается (х)

Нормальное распределение является предельным законом, к которому приближаются другие законы распределения. Мы рассмотрим позднее центральную предельную теорему теории вероятностей, утверждающую, что при достаточно большом n сумма независимых случайных величин ξ₁, ξ₂,..., ξ_n, подчиненным каким угодно законам распределения (при соблюдении некоторых ограничений), будет иметь закон распределения, как угодно близкий к закону нормального распределения.

Числовые характеристики нормального распределения

Таким образом, параметр a является математическим ожиданием, а параметр  - средним квадратическим отклонением случайной величины, имеющей нормальное распределение.

График плотности вероятности - кривая Гаусса (нормальная кривая).

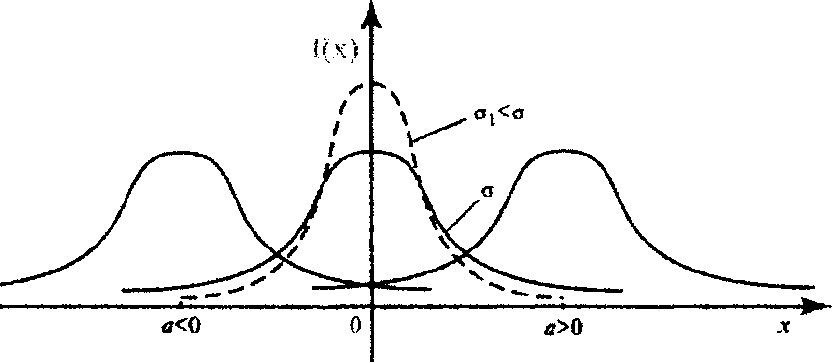
Кривая Гаусса симметрична относительно прямой х = а и имеет максимум при х = а, равный

ветви кривой асимптотически приближаются к оси Ox.

Для нормально распределенной случайной величины функция распределения имеет вид

Ф₀(х) - функция нечетная, т.е. Ф₀ (-х)= - Ф₀ (х) и она затабулирована.

Замечание .

Для того чтобы стандартизировать случайную величину, надо вычесть из нее математическое ожидание и поделить на среднее квадратическое отклонение:

Вероятность попадания в интервал

Следствие:

Нахождение доверительного интервала

Если задана доверительная вероятность р, то

Правило трех сигм

Если задана t = 3, то

Итак,

P(а-3<ξ<а+3)=0,9973,

т.е. практически все значения случайной величины находятся в интервале (а-3; а+3). Вероятность же того, что значения случайной величины попадут вне этого интервала пренебрежимо мала и равна 0,0027.

Пример . Ошибка измерения подчинена нормальному закону с параметрами а =5м, =10м. Найти вероятность того, что измеренное значение расстояния будет отклоняться от истинного не более, чем на 15м.

Решение.

Случайная величина ξ-ошибка измерения,

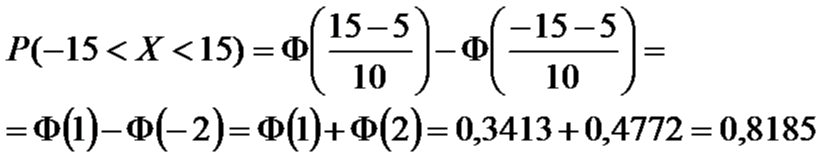
Пример . На станке изготовляются втулки, длина которых L представляет нормально распределенную случайную величину, причем М[L] = 20cм,  = 0,2 см.

Найти:

• Вероятность того, что длина втулки будет отклоняться от ее среднего значения на величину, меньшую 0,3см.

• Длину втулки с вероятностью 0,95.

• Длину втулки с вероятностью 0,9973.

Решение.

• По условию а=20см, =0,2 см.

• так как по условию р = 0,9973, то

31. Функция случайного аргумента. Закон распределения для дискретной случайной величины, вывод формулы для плотности непрерывной случайной величины.

Функции случайных аргументов

Функция η=g(ξ) называется функцией случайного аргумента ξ, если каждому возможному значению случайной величины ξ ставится в соответствие по правилу g одно из возможных значений случайной величины η.

Закон распределения функции случайных аргументов

1.ξ- дискретная случайная величина, т.е. ее ряд распределения имеет вид

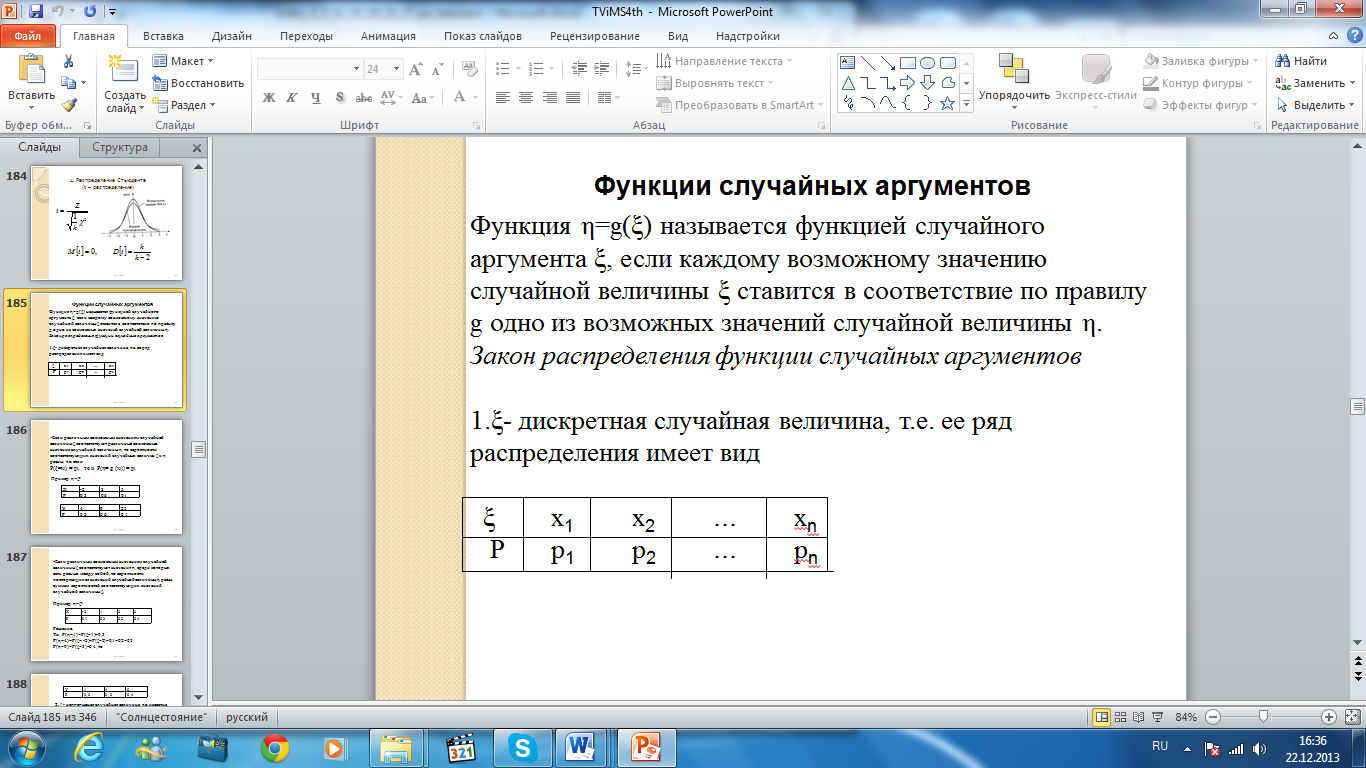
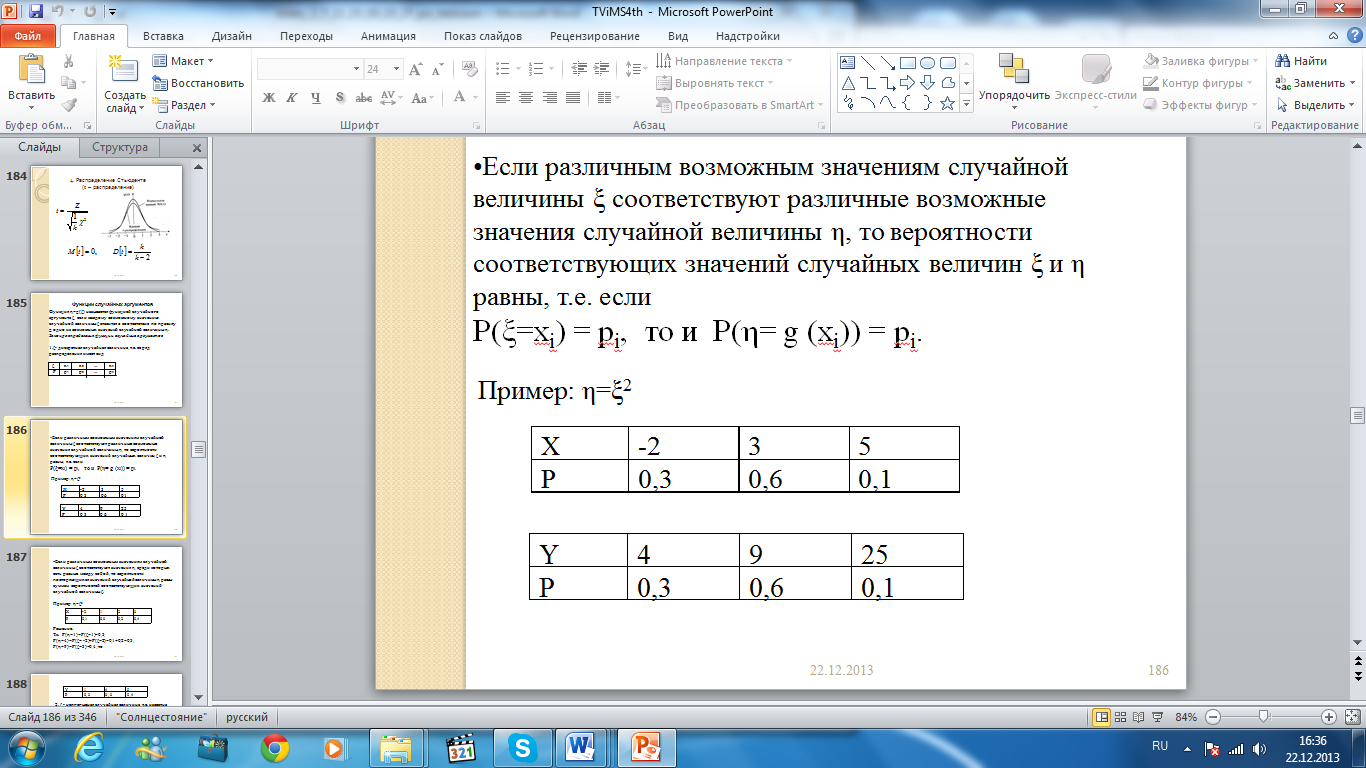
• Если различным возможным значениям случайной величины ξ соответствуют различные возможные значения случайной величины η, то вероятности соответствующих значений случайных величин ξ и η равны, т.е. если

Р(ξ=х_i) = p_i, то и P(η= g (x_i)) = p_i.

Пример: η=ξ²

• Если различным возможным значениям случайной величины ξ соответствуют значения η, среди которых есть равные между собой, то вероятности повторяющихся значений случайной величины η равны суммам вероятностей соответствующих значений случайной величины ξ.

• Пример: η=ξ²

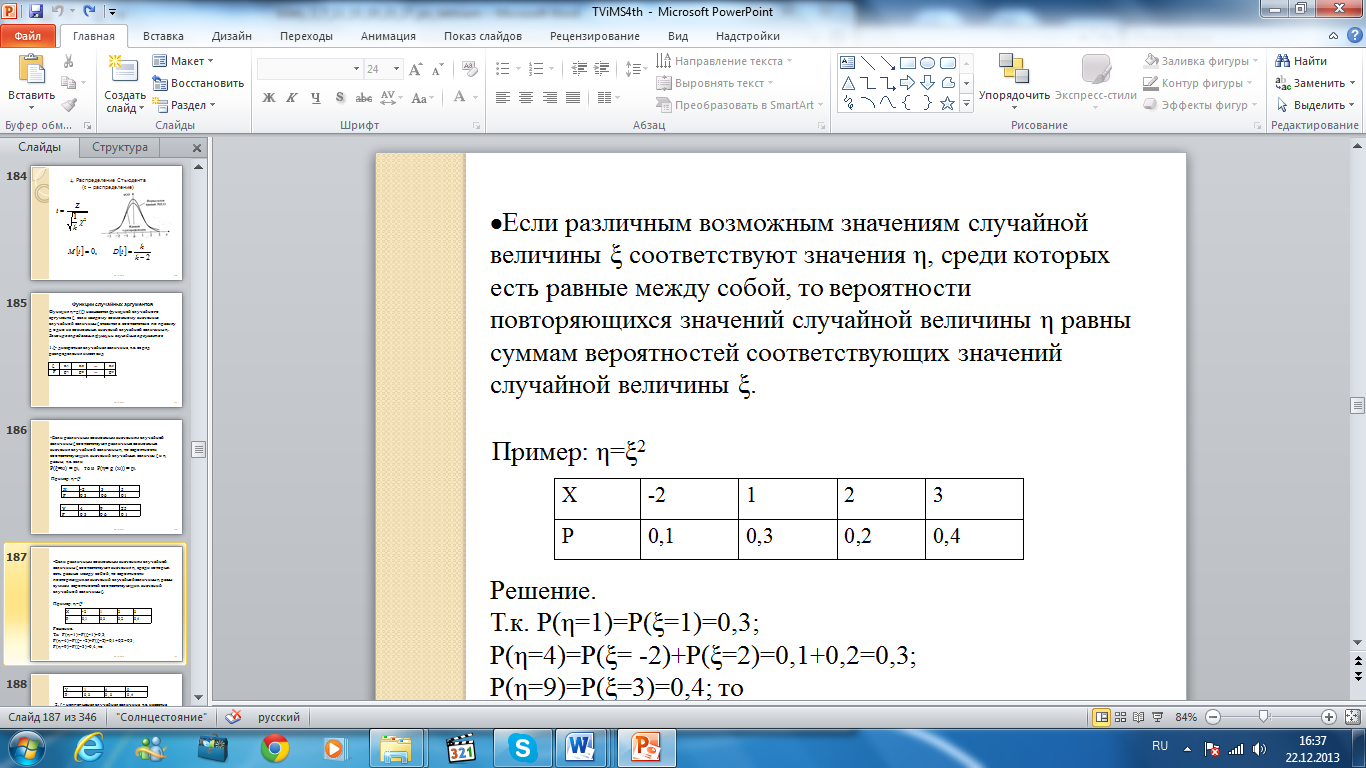
Решение.

Т.к. P(η=1)=P(ξ=1)=0,3;

P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то

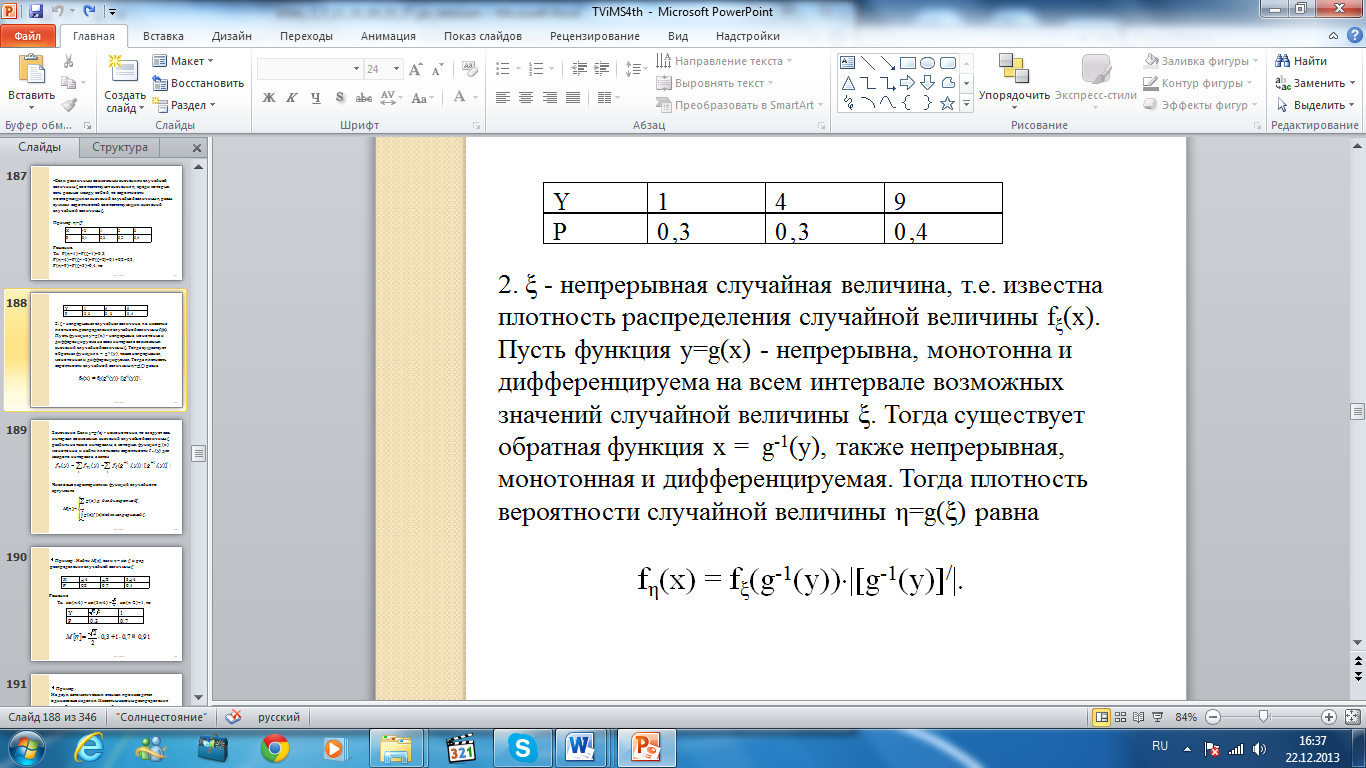
2. ξ - непрерывная случайная величина, т.е. известна плотность распределения случайной величины f_ξ(x). Пусть функция y=g(x) - непрерывна, монотонна и дифференцируема на всем интервале возможных значений случайной величины ξ. Тогда существует обратная функция х = g^-1(у), также непрерывная, монотонная и дифференцируемая. Тогда плотность вероятности случайной величины η=g(ξ) равна

f_η(x) = f_ξ(g^-1(у))|[g^-1(у)]^/|.

Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f _{η i}(y) для каждого интервала, а затем

Числовые характеристики функций случайного аргумента

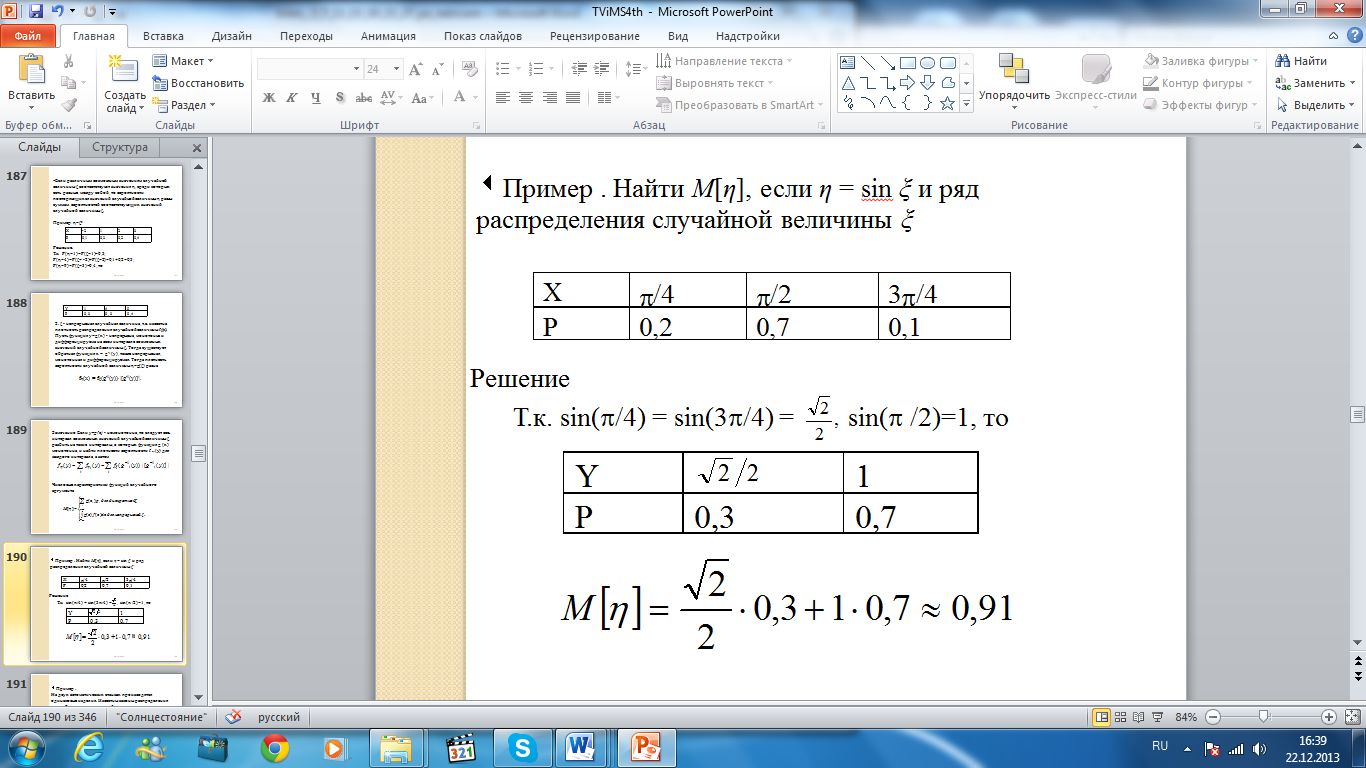
Пример . Найти M[η], если η = sin ξ и ряд распределения случайной величины ξ